您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要講解了python如何實現平穩時間序列的建模,內容清晰明了,對此有興趣的小伙伴可以學習一下,相信大家閱讀完之后會有幫助。
一、平穩序列建模步驟
假如某個觀察值序列通過序列預處理可以判定為平穩非白噪聲序列,就可以利用ARMA模型對該序列進行建模。建模的基本步驟如下:
(1)求出該觀察值序列的樣本自相關系數(ACF)和樣本偏自相關系數(PACF)的值。
(2)根據樣本自相關系數和偏自相關系數的性質,選擇適當的ARMA(p,q)模型進行擬合。
(3)估計模型中位置參數的值。
(4)檢驗模型的有效性。如果模型不通過檢驗,轉向步驟(2),重新選擇模型再擬合。
(5)模型優化。如果擬合模型通過檢驗,仍然轉向不走(2),充分考慮各種情況,建立多個擬合模型,從所有通過檢驗的擬合模型中選擇最優模型。
(6)利用擬合模型,預測序列的將來走勢。
二、代碼實現
1、繪制時序圖,查看數據的大概分布
trainSeting.head() Out[36]: date 2017-10-01 126.4 2017-10-02 82.4 2017-10-03 78.1 2017-10-04 51.1 2017-10-05 90.9 Name: sales, dtype: float64 plt.plot(trainSeting)
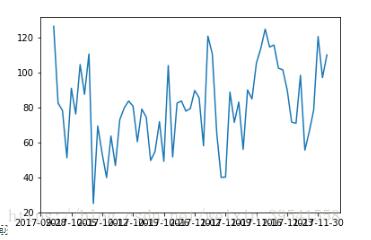
2、平穩性檢驗
'''進行ADF檢驗
adf_test的返回值
Test statistic:代表檢驗統計量
p-value:代表p值檢驗的概率
Lags used:使用的滯后k,autolag=AIC時會自動選擇滯后
Number of Observations Used:樣本數量
Critical Value(5%) : 顯著性水平為5%的臨界值。
(1)假設是存在單位根,即不平穩;
(2)顯著性水平,1%:嚴格拒絕原假設;5%:拒絕原假設,10%類推。
(3)看P值和顯著性水平a的大小,p值越小,小于顯著性水平的話,就拒絕原假設,認為序列是平穩的;大于的話,不能拒絕,認為是不平穩的
(4)看檢驗統計量和臨界值,檢驗統計量小于臨界值的話,就拒絕原假設,認為序列是平穩的;大于的話,不能拒絕,認為是不平穩的
'''
#滾動統計
def rolling_statistics(timeseries):
#Determing rolling statistics
rolmean = pd.rolling_mean(timeseries, window=12)
rolstd = pd.rolling_std(timeseries, window=12)
#Plot rolling statistics:
orig = plt.plot(timeseries, color='blue',label='Original')
mean = plt.plot(rolmean, color='red', label='Rolling Mean')
std = plt.plot(rolstd, color='black', label = 'Rolling Std')
plt.legend(loc='best')
plt.title('Rolling Mean & Standard Deviation')
plt.show(block=False)
##ADF檢驗
from statsmodels.tsa.stattools import adfuller
def adf_test(timeseries):
rolling_statistics(timeseries)#繪圖
print ('Results of Augment Dickey-Fuller Test:')
dftest = adfuller(timeseries, autolag='AIC')
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value #增加后面的顯著性水平的臨界值
print (dfoutput)
adf_test(trainSeting) #從結果中可以看到p值為0.1097>0.1,不能拒絕H0,認為該序列不是平穩序列返回結果如下
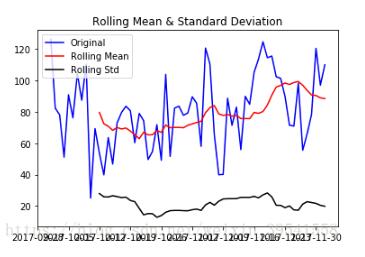
Results of Augment Dickey-Fuller Test: Test Statistic -5.718539e+00 p-value 7.028398e-07 #Lags Used 0.000000e+00 Number of Observations Used 6.200000e+01 Critical Value (1%) -3.540523e+00 Critical Value (5%) -2.909427e+00 Critical Value (10%) -2.592314e+00 dtype: float64
通過上面可以看到,p值小于0.05,可以認為該序列為平穩時間序列。
3、白噪聲檢驗
'''acorr_ljungbox(x, lags=None, boxpierce=False)函數檢驗無自相關 lags為延遲期數,如果為整數,則是包含在內的延遲期數,如果是一個列表或數組,那么所有時滯都包含在列表中最大的時滯中 boxpierce為True時表示除開返回LB統計量還會返回Box和Pierce的Q統計量 返回值: lbvalue:測試的統計量 pvalue:基于卡方分布的p統計量 bpvalue:((optionsal), float or array) – test statistic for Box-Pierce test bppvalue:((optional), float or array) – p-value based for Box-Pierce test on chi-square distribution ''' from statsmodels.stats.diagnostic import acorr_ljungbox def test_stochastic(ts,lag): p_value = acorr_ljungbox(ts, lags=lag) #lags可自定義 return p_value
test_stochastic(trainSeting,[6,12])
Out[62]: (array([13.28395274, 14.89281684]), array([0.03874194, 0.24735042]))
從上面的分析結果中可以看到,延遲6階的p值為0.03<0.05,因此可以拒絕原假設,認為該序列不是白噪聲序列。
4、確定ARMA的階數
(1)利用自相關圖和偏自相關圖
####自相關圖ACF和偏相關圖PACF import statsmodels.api as sm def acf_pacf_plot(ts_log_diff): sm.graphics.tsa.plot_acf(ts_log_diff,lags=40) #ARIMA,q sm.graphics.tsa.plot_pacf(ts_log_diff,lags=40) #ARIMA,p acf_pacf_plot(trainSeting) #查看數據的自相關圖和偏自相關圖
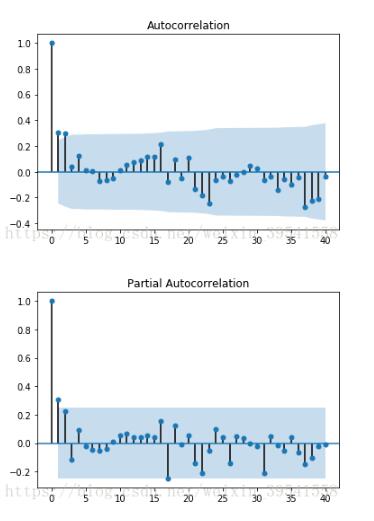
(2)借助AIC、BIC統計量自動確定
##借助AIC、BIC統計量自動確定
from statsmodels.tsa.arima_model import ARMA
def proper_model(data_ts, maxLag):
init_bic = float("inf")
init_p = 0
init_q = 0
init_properModel = None
for p in np.arange(maxLag):
for q in np.arange(maxLag):
model = ARMA(data_ts, order=(p, q))
try:
results_ARMA = model.fit(disp=-1, method='css')
except:
continue
bic = results_ARMA.bic
if bic < init_bic:
init_p = p
init_q = q
init_properModel = results_ARMA
init_bic = bic
return init_bic, init_p, init_q, init_properModel
proper_model(trainSeting,40)#在statsmodels包里還有更直接的函數: import statsmodels.tsa.stattools as st order = st.arma_order_select_ic(ts_log_diff2,max_ar=5,max_ma=5,ic=['aic', 'bic', 'hqic']) order.bic_min_order ''' 我們常用的是AIC準則,AIC鼓勵數據擬合的優良性但是盡量避免出現過度擬合(Overfitting)的情況。所以優先考慮的模型應是AIC值最小的那一個模型。 為了控制計算量,我們限制AR最大階不超過5,MA最大階不超過5。 但是這樣帶來的壞處是可能為局部最優。 timeseries是待輸入的時間序列,是pandas.Series類型,max_ar、max_ma是p、q值的最大備選值。 order.bic_min_order返回以BIC準則確定的階數,是一個tuple類型
返回值如下:
order.bic_min_order
Out[13]: (1, 0)
5、建模
從上述結果中可以看到,可以選擇AR(1)模型
################################模型######################################
# AR模型,q=0
#RSS是殘差平方和
# disp為-1代表不輸出收斂過程的信息,True代表輸出
from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(trainSeting,order=(1,0,0)) #第二個參數代表使用了二階差分
results_AR = model.fit(disp=-1)
plt.plot(trainSeting)
plt.plot(results_AR.fittedvalues, color='red') #紅色線代表預測值
plt.title('RSS:%.4f' % sum((results_AR.fittedvalues-trainSeting)**2))#殘差平方和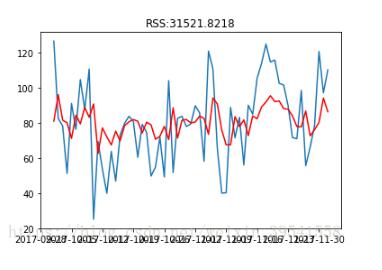
6、預測未來走勢
############################預測未來走勢########################################## # forecast方法會自動進行差分還原,當然僅限于支持的1階和2階差分 forecast_n = 12 #預測未來12個天走勢 forecast_AR = results_AR.forecast(forecast_n) forecast_AR = forecast_AR[0] print (forecast_AR)
print (forecast_ARIMA_log)
[90.49452199 84.05407353 81.92752342 81.22536496 80.99352161 80.9169700380.89169372 80.88334782 80.88059211 80.87968222 80.87938178 80.87928258]
##將預測的數據和原來的數據繪制在一起,為了實現這一目的,我們需要增加數據索引,使用開源庫arrow:
import arrow
def get_date_range(start, limit, level='day',format='YYYY-MM-DD'):
start = arrow.get(start, format)
result=(list(map(lambda dt: dt.format(format) , arrow.Arrow.range(level, start,limit=limit))))
dateparse2 = lambda dates:pd.datetime.strptime(dates,'%Y-%m-%d')
return map(dateparse2, result)
# 預測從2017-12-03開始,也就是我們訓練數據最后一個數據的后一個日期
new_index = get_date_range('2017-12-03', forecast_n)
forecast_ARIMA_log = pd.Series(forecast_AR, copy=True, index=new_index)
print (forecast_ARIMA_log.head())
##繪圖如下
plt.plot(trainSeting,label='Original',color='blue')
plt.plot(forecast_ARIMA_log, label='Forcast',color='red')
plt.legend(loc='best')
plt.title('forecast')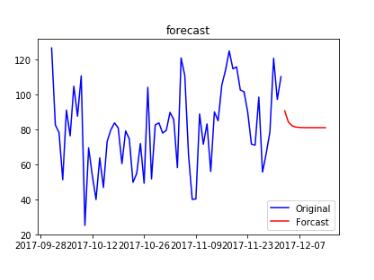
看完上述內容,是不是對python如何實現平穩時間序列的建模有進一步的了解,如果還想學習更多內容,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。