您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容主要講解“String hashCode方法選擇數字31作為乘子的原因是什么”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“String hashCode方法選擇數字31作為乘子的原因是什么”吧!
某天,我在寫代碼的時候,無意中點開了 String hashCode 方法。然后大致看了一下 hashCode 的實現,發現并不是很復雜。但是我從源碼中發現了一個奇怪的數字,也就是本文的主角31。這個數字居然不是用常量聲明的,所以沒法從字面意思上推斷這個數字的用途。后來帶著疑問和好奇心,到網上去找資料查詢一下。在看完資料后,默默的感嘆了一句,原來是這樣啊。那么到底是哪樣呢?在接下來章節里,請大家帶著好奇心和我揭開數字31的用途之謎。
在詳細說明 String hashCode 方法選擇數字31的作為乘子的原因之前,我們先來看看 String hashCode 方法是怎樣實現的,如下:
public int hashCode() { int h = hash; if (h == 0 && value.length > 0) { char val[] = value; for (int i = 0; i < value.length; i++) { h = 31 * h + val[i]; } hhash = h; } return h; }上面的代碼就是 String hashCode 方法的實現,是不是很簡單。實際上 hashCode 方法核心的計算邏輯只有三行,也就是代碼中的 for 循環。我們可以由上面的 for 循環推導出一個計算公式,hashCode 方法注釋中已經給出。如下:
s[0]31^(n-1) + s[1]31^(n-2) + … + s[n-1]
這里說明一下,上面的 s 數組即源碼中的 val 數組,是 String 內部維護的一個 char 類型數組。這里我來簡單推導一下這個公式:
假設 n=3 i=0 -> h = 31 * 0 + val[0] i=1 -> h = 31 * (31 * 0 + val[0]) + val[1] i=2 -> h = 31 * (31 * (31 * 0 + val[0]) + val[1]) + val[2] h = 31*31*31*0 + 31*31*val[0] + 31*val[1] + val[2] h = 31^(n-1)*val[0] + 31^(n-2)*val[1] + val[2]
上面的公式包括公式的推導并不是本文的重點,大家了解了解即可。接下來來說說本文的重點,即選擇31的理由。從網上的資料來看,一般有如下兩個原因:
第一,31是一個不大不小的質數,是作為 hashCode 乘子的優選質數之一。另外一些相近的質數,比如37、41、43等等,也都是不錯的選擇。那么為啥偏偏選中了31呢?請看第二個原因。
第二、31可以被 JVM 優化,31 * i = (i << 5) - i。
上面兩個原因中,第一個需要解釋一下,第二個比較簡單,就不說了。下面我來解釋第一個理由。一般在設計哈希算法時,會選擇一個特殊的質數。至于為啥選擇質數,我想應該是可以降低哈希算法的沖突率。至于原因,這個就要問數學家了,我幾乎可以忽略的數學水平解釋不了這個原因。上面說到,31是一個不大不小的質數,是優選乘子。那為啥同是質數的2和101(或者更大的質數)就不是優選乘子呢,分析如下。
這里先分析質數2。首先,假設 n = 6,然后把質數2和 n 帶入上面的計算公式。并僅計算公式中次數最高的那一項,結果是2^5 = 32,是不是很小。所以這里可以斷定,當字符串長度不是很長時,用質數2做為乘子算出的哈希值,數值不會很大。也就是說,哈希值會分布在一個較小的數值區間內,分布性不佳,最終可能會導致沖突率上升。
上面說了,質數2做為乘子會導致哈希值分布在一個較小區間內,那么如果用一個較大的大質數101會產生什么樣的結果呢?根據上面的分析,我想大家應該可以猜出結果了。就是不用再擔心哈希值會分布在一個小的區間內了,因為101^5 = 10,510,100,501。但是要注意的是,這個計算結果太大了。如果用 int 類型表示哈希值,結果會溢出,最終導致數值信息丟失。盡管數值信息丟失并不一定會導致沖突率上升,但是我們暫且先認為質數101(或者更大的質數)也不是很好的選擇。最后,我們再來看看質數31的計算結果:31^5 = 28629151,結果值相對于32和10,510,100,501來說。是不是很nice,不大不小。
上面用了比較簡陋的數學手段證明了數字31是一個不大不小的質數,是作為 hashCode 乘子的優選質數之一。接下來我會用詳細的實驗來驗證上面的結論,不過在驗證前,我們先看看 Stack Overflow 上關于這個問題的討論,Why does Java's hashCode() in String use 31 as a multiplier?。其中排名第一的答案引用了《Effective Java》中的一段話,這里也引用一下:
The value 31 was chosen because it is an odd prime. If it were even and the multiplication overflowed, information would be lost, as multiplication by 2 is equivalent to shifting. The advantage of using a prime is less clear, but it is traditional. A nice property of 31 is that the multiplication can be replaced by a shift and a subtraction for better performance: `31 * i == (i << 5) - i``. Modern VMs do this sort of optimization automatically.
簡單翻譯一下:
選擇數字31是因為它是一個奇質數,如果選擇一個偶數會在乘法運算中產生溢出,導致數值信息丟失,因為乘二相當于移位運算。選擇質數的優勢并不是特別的明顯,但這是一個傳統。同時,數字31有一個很好的特性,即乘法運算可以被移位和減法運算取代,來獲取更好的性能:31 * i == (i << 5) - i,現代的 Java 虛擬機可以自動的完成這個優化。
排名第二的答案設這樣說的:
As Goodrich and Tamassia point out, If you take over 50,000 English words (formed as the union of the word lists provided in two variants of Unix), using the constants 31, 33, 37, 39, and 41 will produce less than 7 collisions in each case. Knowing this, it should come as no surprise that many Java implementations choose one of these constants.
這段話也翻譯一下:
正如 Goodrich 和 Tamassia 指出的那樣,如果你對超過 50,000 個英文單詞(由兩個不同版本的 Unix 字典合并而成)進行 hash code 運算,并使用常數 31, 33, 37, 39 和 41 作為乘子,每個常數算出的哈希值沖突數都小于7個,所以在上面幾個常數中,常數 31 被 Java 實現所選用也就不足為奇了。
上面的兩個答案完美的解釋了 Java 源碼中選用數字 31 的原因。接下來,我將針對第二個答案就行驗證,請大家繼續往下看。
本節,我將使用不同的數字作為乘子,對超過23萬個英文單詞進行哈希運算,并計算哈希算法的沖突率。同時,我也將針對不同乘子算出的哈希值分布情況進行可視化處理,讓大家可以直觀的看到數據分布情況。本次實驗所使用的數據是 Unix/Linux 平臺中的英文字典文件,文件路徑為 /usr/share/dict/words。
計算哈希算法沖突率并不難,比如可以一次性將所有單詞的 hash code 算出,并放入 Set 中去除重復值。之后拿單詞數減去 set.size() 即可得出沖突數,有了沖突數,沖突率就可以算出來了。當然,如果使用 JDK8 提供的流式計算 API,則可更方便算出,代碼片段如下:
public static Integer hashCode(String str, Integer multiplier) { int hash = 0; for (int i = 0; i < str.length(); i++) { hash = multiplier * hash + str.charAt(i); } return hash; } /** * 計算 hash code 沖突率,順便分析一下 hash code 最大值和最小值,并輸出 * @param multiplier * @param hashs */ public static void calculateConflictRate(Integer multiplier, List<Integer> hashs) { Comparator<Integer> cp = (x, y) -> x > y ? 1 : (x < y ? -1 : 0); int maxHash = hashs.stream().max(cp).get(); int minHash = hashs.stream().min(cp).get(); // 計算沖突數及沖突率 int uniqueHashNum = (int) hashs.stream().distinct().count(); int conflictNum = hashs.size() - uniqueHashNum; double conflictRate = (conflictNum * 1.0) / hashs.size(); System.out.println(String.format("multiplier=%4d, minHash=%11d, maxHash=%10d, conflictNum=%6d, conflictRate=%.4f%%", multiplier, minHash, maxHash, conflictNum, conflictRate * 100)); }結果如下:
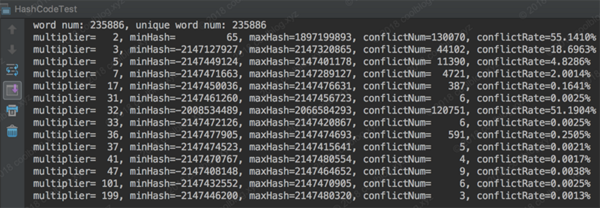
從上圖可以看出,使用較小的質數做為乘子時,沖突率會很高。尤其是質數2,沖突率達到了 55.14%。同時我們注意觀察質數2作為乘子時,哈希值的分布情況。可以看得出來,哈希值分布并不是很廣,僅僅分布在了整個哈希空間的正半軸部分,即 0 ~ 231-1。而負半軸 -231 ~ -1,則無分布。這也證明了我們上面斷言,即質數2作為乘子時,對于短字符串,生成的哈希值分布性不佳。然后再來看看我們之前所說的 31、37、41 這三個不大不小的質數,表現都不錯,沖突數都低于7個。而質數 101 和 199 表現的也很不錯,沖突率很低,這也說明哈希值溢出并不一定會導致沖突率上升。但是這兩個家伙一言不合就溢出,我們認為他們不是哈希算法的優選乘子。最后我們再來看看 32 和 36 這兩個偶數的表現,結果并不好,尤其是 32,沖突率超過了了50%。盡管 36 表現的要好一點,不過和 31,37相比,沖突率還是比較高的。當然并非所有的偶數作為乘子時,沖突率都會比較高,大家有興趣可以自己驗證。
上一節分析了不同數字作為乘子時的沖突率情況,這一節來分析一下不同數字作為乘子時,哈希值的分布情況。在詳細分析之前,我先說說哈希值可視化的過程。我原本是打算將所有的哈希值用一維散點圖進行可視化,但是后來找了一圈,也沒找到合適的畫圖工具。加之后來想了想,一維散點圖可能不合適做哈希值可視化,因為這里有超過23萬個哈希值。也就意味著會在圖上顯示超過23萬個散點,如果不出意外的話,這23萬個散點會聚集的很密,有可能會變成一個大黑塊,就失去了可視化的意義了。所以這里選擇了另一種可視化效果更好的圖表,也就是 excel 中的平滑曲線的二維散點圖(下面簡稱散點曲線圖)。當然這里同樣沒有把23萬散點都顯示在圖表上,太多了。所以在實際繪圖過程中,我將哈希空間等分成了64個子區間,并統計每個區間內的哈希值數量。最后將分區編號做為X軸,哈希值數量為Y軸,就繪制出了我想要的二維散點曲線圖了。這里舉個例子說明一下吧,以第0分區為例。第0分區數值區間是[-2147483648, -2080374784),我們統計落在該數值區間內哈希值的數量,得到 <分區編號, 哈希值數量> 數值對,這樣就可以繪圖了。分區代碼如下:
/** * 將整個哈希空間等分成64份,統計每個空間內的哈希值數量 * @param hashs */ public static Map<Integer, Integer> partition(List<Integer> hashs) { // step = 2^32 / 64 = 2^26 final int step = 67108864; List<Integer> nums = new ArrayList<>(); Map<Integer, Integer> statistics = new LinkedHashMap<>(); int start = 0; for (long i = Integer.MIN_VALUE; i <= Integer.MAX_VALUE; i += step) { final long min = i; final long max = min + step; int num = (int) hashs.parallelStream() .filter(x -> x >= min && x < max).count(); statistics.put(start++, num); nums.add(num); } // 為了防止計算出錯,這里驗證一下 int hashNum = nums.stream().reduce((x, y) -> x + y).get(); assert hashNum == hashs.size(); return statistics; }本文中的哈希值是用整形表示的,整形的數值區間是 [-2147483648, 2147483647],區間大小為 2^32。所以這里可以將區間等分成64個子區間,每個自子區間大小為 2^26。詳細的分區對照表如下:
| 分區編號 | 分區下限 | 分區上限 | 分區編號 | 分區下限 | 分區上限 |
|---|---|---|---|---|---|
| 0 | -2147483648 | -2080374784 | 32 | 0 | 67108864 |
| 1 | -2080374784 | -2013265920 | 33 | 67108864 | 134217728 |
| 2 | -2013265920 | -1946157056 | 34 | 134217728 | 201326592 |
| 3 | -1946157056 | -1879048192 | 35 | 201326592 | 268435456 |
| 4 | -1879048192 | -1811939328 | 36 | 268435456 | 335544320 |
| 5 | -1811939328 | -1744830464 | 37 | 335544320 | 402653184 |
| 6 | -1744830464 | -1677721600 | 38 | 402653184 | 469762048 |
| 7 | -1677721600 | -1610612736 | 39 | 469762048 | 536870912 |
| 8 | -1610612736 | -1543503872 | 40 | 536870912 | 603979776 |
| 9 | -1543503872 | -1476395008 | 41 | 603979776 | 671088640 |
| 10 | -1476395008 | -1409286144 | 42 | 671088640 | 738197504 |
| 11 | -1409286144 | -1342177280 | 43 | 738197504 | 805306368 |
| 12 | -1342177280 | -1275068416 | 44 | 805306368 | 872415232 |
| 13 | -1275068416 | -1207959552 | 45 | 872415232 | 939524096 |
| 14 | -1207959552 | -1140850688 | 46 | 939524096 | 1006632960 |
| 15 | -1140850688 | -1073741824 | 47 | 1006632960 | 1073741824 |
| 16 | -1073741824 | -1006632960 | 48 | 1073741824 | 1140850688 |
| 17 | -1006632960 | -939524096 | 49 | 1140850688 | 1207959552 |
| 18 | -939524096 | -872415232 | 50 | 1207959552 | 1275068416 |
| 19 | -872415232 | -805306368 | 51 | 1275068416 | 1342177280 |
| 20 | -805306368 | -738197504 | 52 | 1342177280 | 1409286144 |
| 21 | -738197504 | -671088640 | 53 | 1409286144 | 1476395008 |
| 22 | -671088640 | -603979776 | 54 | 1476395008 | 1543503872 |
| 23 | -603979776 | -536870912 | 55 | 1543503872 | 1610612736 |
| 24 | -536870912 | -469762048 | 56 | 1610612736 | 1677721600 |
| 25 | -469762048 | -402653184 | 57 | 1677721600 | 1744830464 |
| 26 | -402653184 | -335544320 | 58 | 1744830464 | 1811939328 |
| 27 | -335544320 | -268435456 | 59 | 1811939328 | 1879048192 |
| 28 | -268435456 | -201326592 | 60 | 1879048192 | 1946157056 |
| 29 | -201326592 | -134217728 | 61 | 1946157056 | 2013265920 |
| 30 | -134217728 | -67108864 | 62 | 2013265920 | 2080374784 |
| 31 | -67108864 | 0 | 63 | 2080374784 | 2147483648 |
接下來,讓我們對照上面的分區表,對數字2、3、17、31、101的散點曲線圖進行簡單的分析。先從數字2開始,數字2對于的散點曲線圖如下:
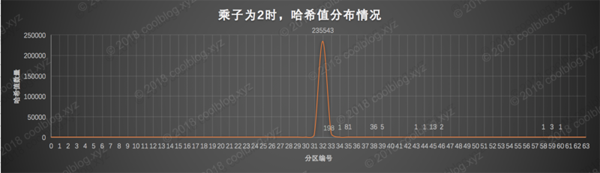
上面的圖還是很一幕了然的,乘子2算出的哈希值幾乎全部落在第32分區,也就是 [0, 67108864)數值區間內,落在其他區間內的哈希值數量幾乎可以忽略不計。這也就不難解釋為什么數字2作為乘子時,算出哈希值的沖突率如此之高的原因了。所以這樣的哈希算法要它有何用啊,拖出去斬了吧。接下來看看數字3作為乘子時的表現:
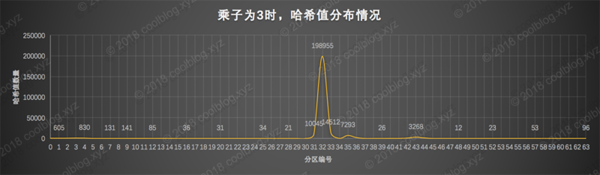
3作為乘子時,算出的哈希值分布情況和2很像,只不過稍微好了那么一點點。從圖中可以看出絕大部分的哈希值最終都落在了第32分區里,哈希值的分布性很差。這個也沒啥用,拖出去槍斃5分鐘吧。在看看數字17的情況怎么樣:
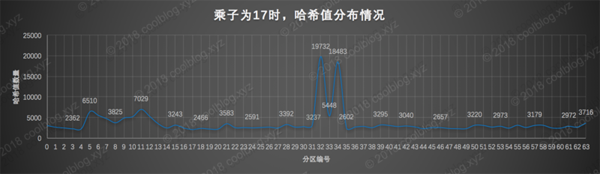
數字17作為乘子時的表現,明顯比上面兩個數字好點了。雖然哈希值在第32分區和第34分區有一定的聚集,但是相比較上面2和3,情況明顯好好了很多。除此之外,17作為乘子算出的哈希值在其他區也均有分布,且較為均勻,還算是一個不錯的乘子吧。
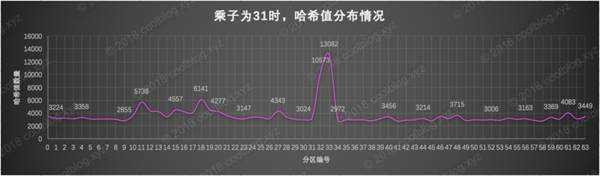
接下來來看看我們本文的主角31了,31作為乘子算出的哈希值在第33分區有一定的小聚集。不過相比于數字17,主角31的表現又好了一些。首先是哈希值的聚集程度沒有17那么嚴重,其次哈希值在其他區分布的情況也要好于17。總之,選31,準沒錯啊。
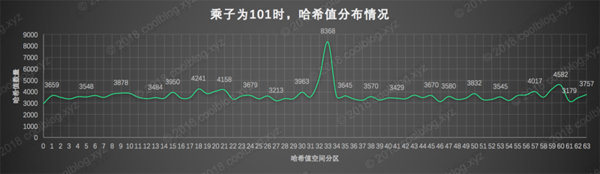
最后再來看看大質數101的表現,不難看出,質數101作為乘子時,算出的哈希值分布情況要好于主角31,有點喧賓奪主的意思。不過不可否認的是,質數101的作為乘子時,哈希值的分布性確實更加均勻。所以如果不在意質數101容易導致數據信息丟失問題,或許其是一個更好的選擇。
到此,相信大家對“String hashCode方法選擇數字31作為乘子的原因是什么”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。