您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
1、梯度下降思想
在數學中的梯度下降是:
xk+1 = xk + λkPk
λk表示步長
Pk表示方向,沿梯度方向下降最快
沿著方向不斷更新x,直到x達到最小
為了得到最好的擬合線,我們的目標是讓損失函數達到最小
因此,引入梯度下降的思想:
條件:有一個J(θ0,θ1)
目標:讓J(θ0,θ1)最小
步驟:
1、初始化θ0,θ1
2、持續改變θ0,θ1的值,讓J(θ0,θ1)越來越小
3、直到得到一個J(θ0,θ1)的最小值
2、梯度下降算法
重復執行: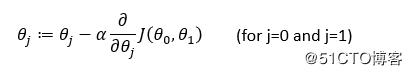
其中:α為學習率,也是步長
求偏導部分(也就是求梯度)是下降方向
線性回歸用到的是同步更新
不論斜率正或負,梯度下降都會逐漸趨向最小值
如果α太小的話,梯度下降會很慢
如果α太大的話,梯度下降會越過最小值,不僅不會收斂,還有可能發散
即使α是固定不變的,梯度下降也會逐漸到一個最低點,因為隨著梯度下降迭代次數的遞增,斜率會趨于平緩,也就是說,倒數部分會慢慢變小
至于怎么選取α,下面會講到
3、線性回歸的梯度下降
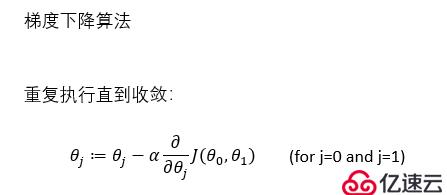

四、三種梯度下降
1、批梯度下降
批梯度下降Bath Gradient Descent:
指每下降一步,使用所有的訓練集來計算梯度值
import numpy as np
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), X]
#print(X_b)
#學習率α
learning_rate = 0.1
#通常在做機器學習的時候,一般不會等到它收斂,太浪費時間,所以會設置一個收斂次數n_iterations
n_iterations = 1000
#樣本數
m = 100
#1.初始化 θ0 , θ1
theta = np.random.randn(2, 1)
count = 0
#4. 不會設置閾值,之間設置超參數,迭代次數,迭代次數到了,我們就認為收斂了
for iteration in range(n_iterations):
count += 1
#2. 接著求梯度gradient
gradients = 1.0/m * X_b.T.dot(X_b.dot(theta)-y)
#3. 應用公式不斷更新theta值
theta = theta - learning_rate * gradients
print(count)
print(theta)運行結果: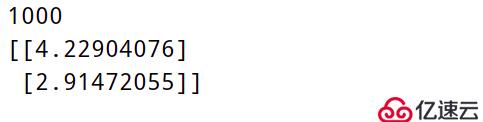
這里其實我還是想拿矩陣來解釋一下
函數 hθ(x) = -4000 + 12000x
當x = 120 , 150 時,方程可由矩陣表示為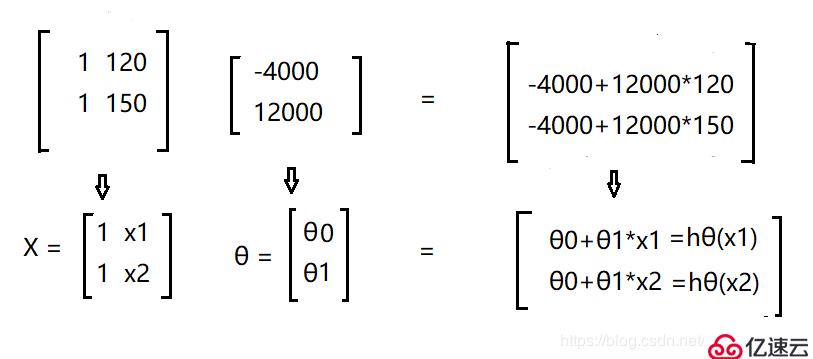
代碼中:
np.c_[ ] 表示把2個維度相同的矩陣拼在一起
np.ones((100,1)) 表示100行1列元素全是1的矩陣
np.dot(a,b) 表示矩陣a和b點乘,或者寫為 a.dot(b)
.T 表示求矩陣的轉置
計算梯度的這段代碼: gradients = 1.0/m * X_b.T.dot(X_b.dot(theta)-y)
為了方便起見,就以2個樣本數量x1,x2 來解釋吧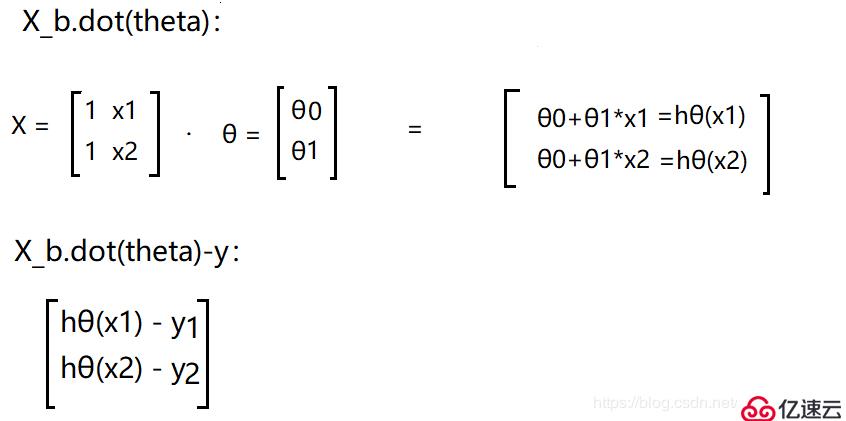
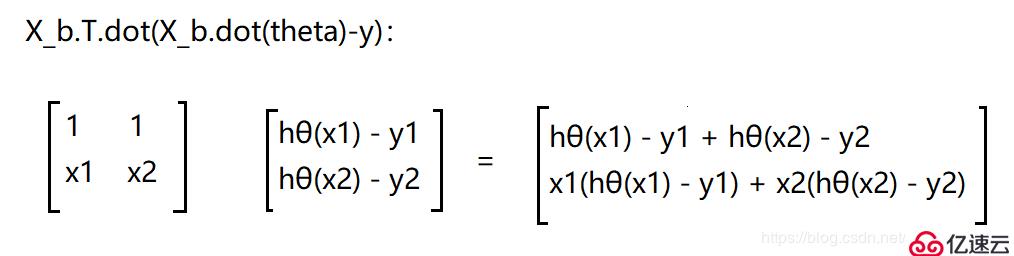
再除以m : 1.0/m X_b.T.dot(X_b.dot(theta)-y) ,就相當于紅框中的這一部分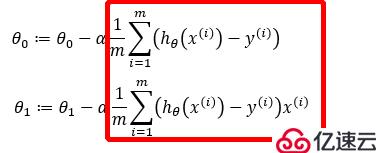
因此:不斷更新的theta值就為:
theta = theta - learning_rate gradients
2、隨機梯度下降
隨機梯度下降Stochastic Gradient Descent
指的是每下降一步,使用一條訓練集來計算梯度值
把m個樣本分成m份,每次用1份做梯度下降;也就是說,當有m個樣本時,批梯度下降只能做一次梯度下降,但是隨機梯度下降可以做m次
有一個概念:epoch 輪次
1 epoch = 1次遍歷所有的數據
對于批梯度下降來說,1次梯度下降就是1epoch
對于隨機梯度下降來說,需要做m次才是1epoch
import numpy as np
import random
x = 2 * np.random.rand(100, 1)
y = 4 + 3 * x + np.random.randn(100 ,1)
X = np.c_[np.ones((100, 1)), x]
n_epochs = 500 # 輪次
learning_rate = 0.1 # 學習率
m = 100 # 樣本數
num = [i for i in range(m)] # 列表num:0 ~ 99
theta = np.random.rand(2, 1) # 初始化theta值
#做500epoch,一次處理1條,一個epoch循環100次
for epoch in range(n_epochs):
rand = random.sample(num, m) # 在列表num中隨機選取100個數字,其實是將順序打亂
#print(rand)
for i in range(m):
random_index = rand[i] # rand是一個列表,拿到列表中的每一個元素作為索引
xi = X[random_index: random_index+1] # 隨機選取一個樣本
yi = y[random_index: random_index+1]
gradients = xi.T.dot(xi.dot(theta) - yi) #只選取了1個樣本,所以乘以的是 1/1
theta = theta - learning_rate * gradients
print(theta)運行結果:
3、Mini-Batch梯度下降
Mini-Batch Gradient Descent
指的是每下降一步,使用一部分的訓練集來計算梯度值
如果mini-batch 大小 = m:它就是批梯度下降
如果mini-batch 大小 = 1 :它就是隨機梯度下降
如果 1 < mini-batch大小 < m :它就是Mini-Batch梯度下降
import numpy as np
import random
x = 2 * np.random.rand(100, 1)
y = 4 + 3 * x + np.random.randn(100 ,1)
X = np.c_[np.ones((100, 1)), x]
n_epochs = 500 # 輪次
learning_rate = 0.1 # 學習率
m = 100 # 樣本數
theta = np.random.rand(2, 1) # 初始化theta值
batch_num = 5 # 循環5次
batch_size = m // 5 # 一次處理20條
#做500epoch, 一次處理20條,一個epoch循環5次
for epoch in range(n_epochs):
for i in range(batch_num): # 循環5次
start = i * batch_size
end = (i + 1) * batch_size
xi = X[start: end]
yi = y[start: end]
gradients = 1 / batch_size * xi.T.dot(xi.dot(theta) - yi) #選取了batch_size個樣本,所以乘以 1/batch_size
theta = theta - learning_rate * gradients
print(theta)運行結果:
4、三種梯度下降比較
梯度下降類別 速度 準確度
批梯度下降 最慢 最準確
Mini-Batch梯度下降 中等 中等
隨機梯度下降 最快 不準確
如何選擇:
隨機梯度下降會喪失向量帶來的加速,所以我們不太會用隨機梯度下降
當訓練集比較小時,使用批梯度下降(小于2000個)
當訓練集比較大時,使用Mini-Batch梯度下降
一般的Mini-Batch size為:64,128,256,512,1024
Mini-Batch size要適用CPU/GPU的內存
5、學習率衰減
我們在以上代碼中還提到了一個概念 α 學習率
一般我們選擇α時,可以嘗試 :1,0.1,0.2,0.3…
在做Mini-Batch的時候,因為噪聲的原因,可能訓練,結果不是收斂的,而是在最低點附近擺動,因為α是固定不變的,如果我們要解決這個問題,就需要減少學習率,讓步伐不斷減小,讓他在盡量小的范圍內晃動
因此我們在設置了α初始值后,還可以設置它的衰減率,通過不斷更新學習率,從而達到要求
實現方法: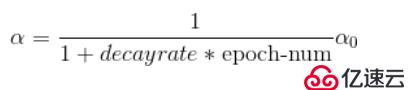
學習率初始值: a0
衰減率:decay_rate
代數:epoch_num,第幾次循環
import numpy as np
import random
x = 2 * np.random.rand(100, 1)
y = 4 + 3 * x + np.random.randn(100 ,1)
X = np.c_[np.ones((100, 1)), x]
a0 = 0.1 # 學習率初始值
decay_rate = 1 # 衰減率
#更新學習率
def learning_schedule(epoch_num):
return (1.0 / (1 + decay_rate * epoch_num )) * a0
n_epochs = 500 # 輪次
m = 100 # 樣本數
theta = np.random.rand(2, 1) # 初始化theta值
batch_num = 5 # 循環5次
batch_size = m // 5 # 一次處理20條
#做500epoch, 一次處理20條,一個epoch循環5次
for epoch in range(n_epochs):
for i in range(batch_num): # 循環5次
start = i * batch_size
end = (i + 1) * batch_size
xi = X[start: end]
yi = y[start: end]
gradients = (1 / batch_size) * xi.T.dot(xi.dot(theta) - yi)
learning_rate = learning_schedule(i) # 更新的學習率
theta = theta - learning_rate * gradients
print(theta)實現學習率衰減還有其他幾種方法: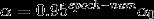
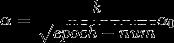
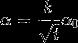
五、多變量線性回歸
1、多變量線性回歸模型
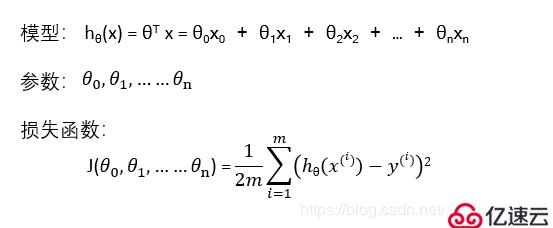
#encoding:utf-8
"""
多項式回歸
"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X ** 2 + X + 2 + np.random.randn(m, 1)
plt.plot(X, y, 'b.')
# plt.show()
d = {1: 'g-', 2: 'r+', 10: 'y*'}
for i in d:
#include_bias 可以理解為w0 =False 意思就是不要w0
poly_features = PolynomialFeatures(degree=i, include_bias=False)
"""
fit 和 fit_transform的區別
fit: 簡單來說,就是求得訓練集X的均值,方差,最大值,最小值這些訓練集X固有的屬性
fit_transform: 首先fit,然后在此基礎上,進行標準化,降維,歸一化等操作
"""
X_poly = poly_features.fit_transform(X)
#print(X[0])
#print(X_poly[0])
#print(X_poly[:, 0])
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
print(lin_reg.intercept_, lin_reg.coef_)
y_predict = lin_reg.predict(X_poly)
plt.plot(X_poly[:, 0], y_predict, d[i])
plt.show()2、多元梯度下降

import numpy as np
import random
from sklearn.linear_model import LinearRegression
x1=np.array([1,1,1])
x2=np.array([1,1,2])
x3=np.array([2,2,2])
x4=np.array([1,2,3])
x5=np.array([2,3,4])
x=np.c_[x1,x2,x3,x4,x5]
y=np.array([3,4,6,6,9])
lin_reg=LinearRegression()
lin_reg.fit(x.T,y)
print(lin_reg.intercept_,lin_reg.coef_)
x_new=np.array([[12,15,17]])
print(lin_reg.predict(x_new))免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。