您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇文章給大家分享的是有關python 中如何實現一個排序算法,小編覺得挺實用的,因此分享給大家學習,希望大家閱讀完這篇文章后可以有所收獲,話不多說,跟著小編一起來看看吧。
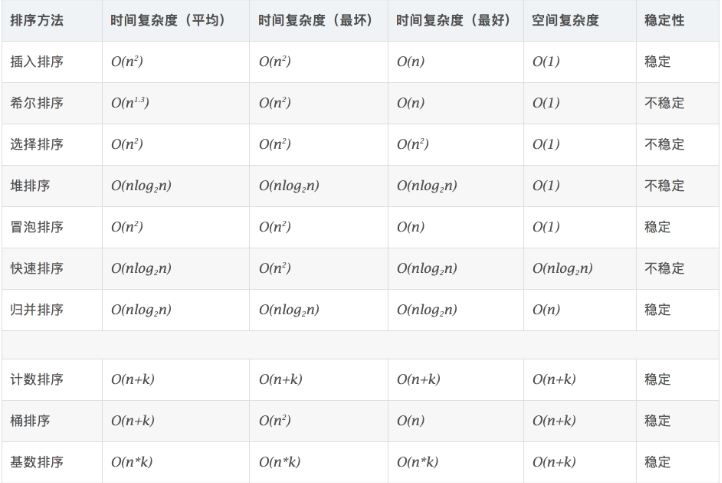
排序分為兩類,比較類排序和非比較類排序,比較類排序通過比較來決定元素間的相對次序,其時間復雜度不能突破O(nlogn);非比較類排序可以突破基于比較排序的時間下界,缺點就是一般只能用于整型相關的數據類型,需要輔助的額外空間。
要求能夠手寫時間復雜度位O(nlogn)的排序算法:快速排序、歸并排序、堆排序
1.冒泡排序
思想:相鄰的兩個數字進行比較,大的向下沉,最后一個元素是最大的。列表右邊先有序。
時間復雜度$O(n^2)$,原地排序,穩定的
def bubble_sort(li:list):
for i in range(len(li)-1):
for j in range(i + 1, len(li)):
if li[i] > li[j]:
li[i], li[j] = li[j], li[i]2.選擇排序
思想:首先找到最小元素,放到排序序列的起始位置,然后再從剩余元素中繼續尋找最小元素,放到已排序序列的末尾,以此類推,直到所有元素均排序完畢。列表左邊先有序。
時間復雜度$O(n^2)$,原地排序,不穩定
def select_sort(nums: list):
for i in range(len(nums) - 1):
min_index = i
for j in range(i + 1, len(nums)):
if nums[j] < nums[i]:
min_index = j
nums[i], nums[min_index] = nums[min_index], nums[i] 3.插入排序
思想:構建有序序列,對于未排序數據,在已排序序列中從后向前掃描,找到相應位置并插入。列表左邊先有序。
時間復雜度$O(n^2)$,原地排序,穩定
def insert_sort(nums: list):
for i in range(len(nums)):
current = nums[i]
pre_index = i - 1
while pre_index >= 0 and nums[pre_index] > current:
nums[pre_index + 1] = nums[pre_index]
pre_index -= 1
nums[pre_index + 1] = current4.希爾排序
思想:插入排序的改進版,又稱縮小增量排序,將待排序的列表按下標的一定增量分組,每組分別進行直接插入排序,增量逐漸減小,直到為1,排序完成
時間復雜度$O(n^{1.5})$,原地排序,不穩定
def shell_sort(nums: list):
gap = len(nums) >> 1
while gap > 0:
for i in range(gap, len(nums)):
current = nums[i]
pre_index = i - gap
while pre_index >= 0 and nums[pre_index] > current:
nums[pre_index + gap] = nums[pre_index]
pre_index -= gap
nums[pre_index + gap] = current
gap >>= 15.快速排序
思想:遞歸,列表中取出第一個元素,作為標準,把比第一個元素小的都放在左側,把比第一個元素大的都放在右側,遞歸完成時就是排序結束的時候
時間復雜度$O(nlogn)$,空間復雜度$O(logn)$,不穩定
def quick_sort(li:list):
if li == []:
return []
first = li[0]
# 推導式實現
left = quick_sort([l for l in li[1:] if l < first])
right = quick_sort([r for r in li[1:] if r >= first])
return left + [first] + right6.歸并排序
思想:分治算法,拆分成子序列,使用歸并排序,將排序好的子序列合并成一個最終的排序序列。關鍵在于怎么合并:設定兩個指針,最初位置分別為兩個已經排序序列的起始位置,比較兩個指針所指向的元素,選擇相對小的元素放到合并空間,并將該指針移到下一位置,直到某一指針超出序列尾,將另一序列所剩下的所有元素直接復制到合并序列尾。
時間復雜度$O(nlogn)$,空間復雜度O(n),不穩定
二路歸并
def merge_sort(nums: list):
if len(nums) <= 1:
return nums
mid = len(nums) >> 1
left = merge_sort(nums[:mid]) # 拆分子問題
right = merge_sort(nums[mid:])
def merge(left, right): # 如何歸并
res = []
l, r = 0, 0
while l < len(left) and r < len(right):
if left[l] <= right[r]:
res.append(left[l])
l += 1
else:
res.append(right[r])
r += 1
res += left[l:]
res += right[r:]
return res
return merge(left, right)7.堆排序
思想:根節點最大,大頂堆,對應升序,根節點最小,小頂堆。
時間復雜度$O(nlogn)$,原地排序,穩定
def heap_sort(nums: list):
def heapify(parent_index, length, nums):
temp = nums[parent_index] # 根節點的值
chile_index = 2 * parent_index + 1 # 左節點,再加一為右節點
while chile_index < length:
if chile_index + 1 < length and nums[chile_index + 1] > nums[chile_index]:
chile_index = chile_index + 1
if temp > nums[chile_index]:
break
nums[parent_index] = nums[chile_index] # 使得根節點最大
parent_index = chile_index
chile_index = 2 * parent_index + 1
nums[parent_index] = temp
for i in range((len(nums) - 2) >> 1, -1, -1):
heapify(i, len(nums), nums) # 1.建立大根堆
for j in range(len(nums) - 1, 0, -1):
nums[j], nums[0] = nums[0], nums[j]
heapify(0, j, nums) # 2.堆排序,為升序
if __name__ == '__main__':
nums = [89, 3, 3, 2, 5, 45, 33, 67] # [2, 3, 3, 5, 33, 45, 67, 89]
heap_sort(nums)
print(nums) 以上就是python 中如何實現一個排序算法,小編相信有部分知識點可能是我們日常工作會見到或用到的。希望你能通過這篇文章學到更多知識。更多詳情敬請關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。