您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章給大家分享的是有關C語言實現牛頓迭代法解方程的示例的內容。小編覺得挺實用的,因此分享給大家做個參考,一起跟隨小編過來看看吧。
C語言實現牛頓迭代法解方程詳解
利用迭代算法解決問題,需要做好以下三個方面的工作:
一、確定迭代變量
在可以用迭代算法解決的問題中,我們可以確定至少存在一個可直接或間接地不斷由舊值遞推出新值的變量,這個變量就是迭代變量。
二、建立迭代關系式
所謂迭代關系式,指如何從變量的前一個值推出其下一個值的公式(或關系)。迭代關系式的建立是解決迭代問題的關鍵,通常可以使用遞推或倒推的方法來完成。
三、對迭代過程進行控制
在什么時候結束迭代過程?這是編寫迭代程序必須考慮的問題。不能讓迭代過程無休止地執行下去。迭代過程的控制通常可分為兩種情況:一種是所需的迭代次數是個確定的值,可以計算出來;另一種是所需的迭代次數無法確定。對于前一種情況,可以構建一個固定次數的循環來實現對迭代過程的控制;對于后一種情況,需要進一步分析得出可用來結束迭代過程的條件。
接下來,我介紹一種迭代算法的典型案例----牛頓-拉夫遜(拉弗森)方法
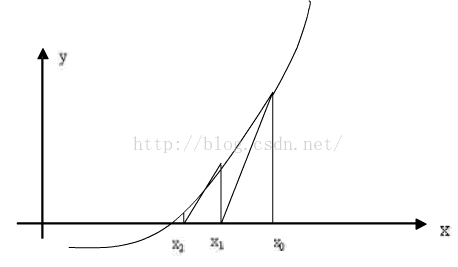
牛頓-拉夫遜(拉弗森)方法,又稱牛頓迭代法,也稱牛頓切線法:先任意設定一個與真實的根接近的值x0作為第一次近似根,由x0求出f(x0),過(x0,f(x0))點做f(x)的切線,交x軸于x1,把它作為第二次近似根,再由x1求出f(x1),過(x1,f(x1))點做f(x)的切線,交x軸于x2,……如此繼續下去,直到足夠接近(比如|x- x0|<1e-6時)真正的根x*為止。
而f '(x0)=f(x0)/( x1- x0)
所以 x1= x0- f(x0)/ f ' (x0)。
我們來看一副從網上找到的圖:
接下來,我們來看一個例子:
我們還是直接上代碼:
例子:用牛頓迭代法求下列方程在值等于2.0附近的根:2x3-4x2+3x-6=0。
#include <stdio.h>
#include <math.h>
int main(void)
{
float x,x0,f,f1;
x = 2.0;
do{
x0=x;
f=2*x0*x0*x0-4*x0*x0+3*x0-6;
f1=6*x0*x0-8*x0+3;
x=x0-f/f1;
//函數fabs:求浮點數x的絕對值
//說明:計算|x|, 當x不為負時返回 x,否則返回 -x
}while(fabs(x-x0)>=1e-5);
printf ("%f\n",x);
return 0 ;
}執行結果:
當x=1.5時,方程2x3-4x2+3x-6=0。附近的根為2.000000 。
感謝各位的閱讀!關于“C語言實現牛頓迭代法解方程的示例”這篇文章就分享到這里了,希望以上內容可以對大家有一定的幫助,讓大家可以學到更多知識,如果覺得文章不錯,可以把它分享出去讓更多的人看到吧!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。