Python數據處理之Sympy如何實現解方程

小編給大家分享一下Python數據處理之Sympy如何實現解方程，相信大部分人都還不怎么了解，因此分享這篇文章給大家參考一下，希望大家閱讀完這篇文章后大有收獲，下面讓我們一起去了解一下吧！

官方教程

https://docs.sympy.org/latest/tutorial/solvers.html

（一）求解多元一次方程-solve()

1.說明：

解多元一次方程可以使用solve()，在sympy里，等式是用Eq()來表示，

例如：2x=42x=4 表示為：Eq(x*2, 4)

2.源代碼：

"""
 解下列二元一次方程
 2x-y=3
 3x+y=7
"""
# 導入模塊
from sympy import *
# 將變量符號化
x = Symbol('x')
y = Symbol('y')
z = Symbol('z')
# 解一元一次方程
expr1 = x*2-4
r1 = solve(expr1, x)
r1_eq = solve(Eq(x*2, 4), x)
print("r1:", r1)
print("r1_eq:", r1_eq)
# 解二元一次方程
expr2 = [2*x-y-3, 3*x+y-7]
r2 = solve(expr2, [x, y])
print("r1:", r2)
# 解三元一次方程
f1 = x+y+z-2
f2 = 2*x-y+z+1
f3 = x+2*y+2*z-3
r3 = solve([f1, f2, f3], [x, y, z])
print("r3:", r3)

3.輸出：

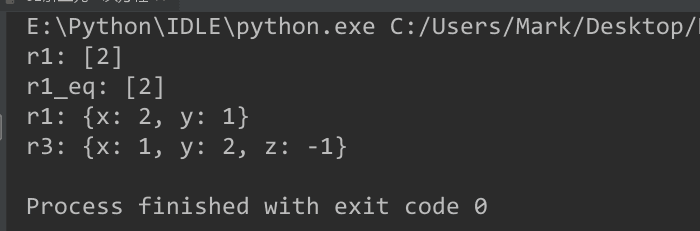
（二）解線性方程組-linsolve（）

1.說明：

在sympy中，解線性方程組有三種形式：

默認等式為0的形式：linsolve(eq, [x, y, z])

矩陣形式：linsolve(eq, [x, y, z])

增廣矩陣形式：linsolve(A，b, x, y, z)

2.源代碼：

"""
  x+y+z-2=0
  2x-y+z+1=0
  x+2y+2z-3=0
"""
from sympy import *
x, y, z = symbols("x y z")
# 默認等式為0的形式
print("======默認等式為0的形式 =======")
eq = [x+y+z-2, 2*x-y+z+1, x+2*y+2*z-3]
result = linsolve(eq, [x, y, z])
print(result)
print(latex(result))
# 矩陣形式
print("======矩陣形式 =======")
eq = Matrix(([1, 1, 1, 2], [2, -1, 1, -1], [1, 2, 2, 3]))
result = linsolve(eq, [x, y, z])
print(result)
print(latex(result))
# 增廣矩陣形式
print("======增廣矩陣形式 =======")
A = Matrix([[1, 1, 1], [2, -1, 1], [1, 2, 2]])
b = Matrix([[2], [-1], [3]])
system = A, b
result = linsolve(system, x, y, z)
print(result)
print(latex(result))

3.輸出：

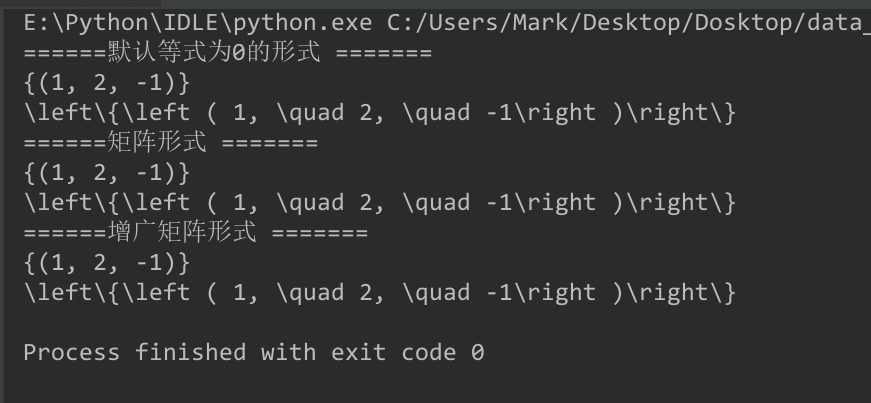
（三）解非線性方程組-nonlinsolve（）

1.說明：

nonlinsolve()用于求解非線性方程組，例如二次方，三角函數，，，等方程

2.源代碼：

"""
  x**2+y**2-2=0
  x**3+y**3=0
"""
import sympy as sy
x, y = sy.symbols("x y")
eq = [x**2+y**3-2, x**3+y**3]
result = sy.nonlinsolve(eq, [x, y])
print(result)
print(sy.latex(result))

3.輸出：

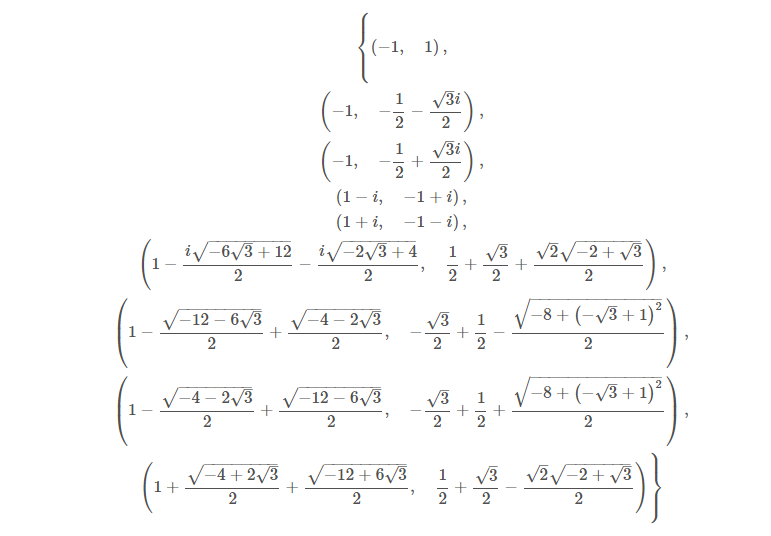
（四）求解微分方程-dsolve（）

1.說明：

求解微分方程使用dsolve（），注意：

f = symbols('f', cls=Function)的作用是聲明f()是一個函數。

2.源代碼：

from sympy import *
# 初始化
x = symbols('x')
f = symbols('f', cls=Function)
# 表達式
expr1 = Eq(f(x).diff(x, x) - 2*f(x).diff(x) + f(x), sin(x))
# 求解微分方程
r1 = dsolve(expr1, f(x))
print(r1)
print("原式：", latex(expr1))
print("求解后：", latex(r1))

3.輸出：

原式：

f(x)?2ddxf(x)+d2dx2f(x)=sin(x)
f(x)?2ddxf(x)+d2dx2f(x)=sin?(x)

解微分后：

f(x)=(C1+C2x)ex+cos(x)2
f(x)=(C1+C2x)ex+cos?(x)2

以上是“Python數據處理之Sympy如何實現解方程”這篇文章的所有內容，感謝各位的閱讀！相信大家都有了一定的了解，希望分享的內容對大家有所幫助，如果還想學習更多知識，歡迎關注億速云行業資訊頻道！