您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
問題:n個元素的向量V循環移位(以左移為例)i個位置,例如12345循環移動2個位置得到34512.
問題本身非常簡單,以至于我們一看到問題就能想到對應的解決策略:申請i個字節的動態存儲,將向量區間[0,i-1]的i個元素存儲至臨時存儲器,之后將[i,n]的n-i+1個元素向左移動i個位置,并將臨時存儲器中的i個元素寫回原向量區間中[n-i+1,n]。但如果我們強加一些限制:在現有可申請內存的總量k << i以及所要求的時間復雜度為O(n)的情況下如何實現循環移位?問題的復雜度似乎就上了一個量級。而之所以寫這篇文章,很大程度上是因為接下來要介紹的三種方法帶來了對問題本質更深入的思考。
方法一(姑且稱之為求模法):借助一個臨時變量temp,temp ← V[0],V[0] ← V[i%n],V[i%n] ← V[(2i)%n]…直到(ki)%n =0時,此時所要完成的操作即為V[((k-1)i)%n] ← V[0],而由于變量V[0]的值在被V[i%n]覆蓋之前已存入temp,取而代之的操作即為:V[((k-1)i)%n] ← temp。圖解表示為(圖示的移位個數為i=3):
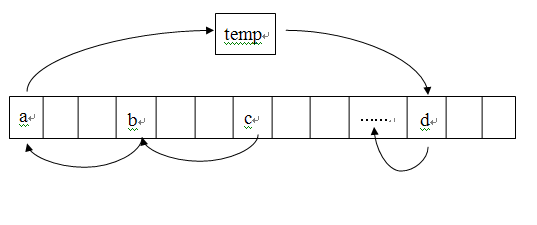
整個操作過程借助一個臨時變量,經過n次左右的操作即完成整個移位過程,時間復雜度滿足O(n)。事實上,向量中所有的元素都進行了移位操作,因此如果當完成V[((k-1)i)%n] ← temp操作時,仍有元素未完成移動,此時從V[1]開始再次進行移動。因為如果沒有移動全部的元素,則說明最初的i個元素將分為m(m>1)個等價類,所以從V[1]開始再次移動是可行的,這歸功于等價類的性質:任何求模等價類聚集中每個集合中的每個元素間隔的長度相等。所以若0和1同屬一個等價類,則該等價類必然包含所有i個元素。
上述過程的偽碼表示為:
/*LOOPSHIFT(V,i)*/
cnt←0
j←-1
while cnt≠length[V]
do j←j+1
temp←V[j]
k←i+j
while k%n≠j
do V[(k-i)%n]←V[k%n]
k←k+i
cnt←cnt+1
V[(k-i)%n]←temp
cnt←cnt+1
在繼續深入考慮之前先思考以下兩種情況:①在13個元素中循環移動5個元素(12/5) ②在14個元素中移動4個元素(14/4),其中⌈⌉表示上取整,⌊⌋表示下取整。
1)在13/5這種情況中,由于(⌈12/5⌉)×5-12=3,每次在5個元素中以2進行循環迭代,在[0,4]這5個元素中的迭代次序為(不考慮向量中的其他元素):0→3→1(6%5)→4(9%5)→2(12%5)→0(15%5),因此最終通過上述代碼的一次內層循環即可完成整個移位操作。
2)在14/4這種情況中,由于(⌈14/4⌉)×4-14=2,每次在4個元素中也以2進行循環迭代,在[0,3]這5個元素中的迭代次序為:0→2→0(4%2)→1(退出內層循環,簡單從下標為1的元素重新開始移動)→3→1(5%2),因此最后在外層執行兩次迭代才最終完成整個移位操作。
通過這兩個例子可以發現外層的迭代次數(即等價類的個數)最終和整個向量的長度以及所要移位的個數有關,具體的關系為:cnt = gcd(n,i) 其中n=length[A],cnt為外層迭代的次數。
由于任何求模等價類聚集中每個集合中的元素間隔的長度相等(由上可知,即實際過程中未進行模運算之前的值),據此證明過程如下:
因為length[V]=n且移位個數為i,因此必然存在大于等于n且被i整除的數k=⌈n/i⌉×i
由n= α×gcd(n,i)且i=β×gcd(n,i),k=⌈n/i⌉×β×gcd(n,i)
因此在i個元素上每次移位的個數為iter=k-n=(⌈n/i⌉×β-α)×gcd(n,i),即iter能被gcd(n,i)整除
由于對元素求模各等價類的個數即為等價類中每個元素的間隔長度,因此實際在i個元素中進行iter個移位所得的等價類即為:
i×iter/lcm(n,i)=gcd(i,iter)=gcd(i,(⌈n/i⌉×β-α)×gcd(n,i)),由于i=β×gcd(n,i)可得gcd(β,⌈n/i⌉×β-α)=1
由此可知gcd(i,iter)=gcd(n,i),因此結論得證,共有cnt=gcd(n,i)個等價類,每個等價類的代表所構成的集合為{0,1,…,cnt-1}(用近世代數的術語來說,也就是旋轉產生的置換群的陪集個數)。
因此上述偽碼可重寫為:
/*LOOPSHIFT(V,i) --gcd version*/
for cnt←0 to gcd(n,i)-1 /*n=length[V], "cnt←0 to n"means assign cnt in [0,n] */
do temp←V[cnt]
k←i
for j←1 to (length[V]/gcd(n,i))-1
do V[(k-i)%n]←V[k%n]
k←k+i
V[(k-i)%n]←temp
第二種方法(遞歸法):令V=ab(a為要移位的個數,length[a]與length[b]不一定相等),則旋轉向量V實際就是交換向量ab得到ba,假定length[a]<length[b],分解向量b=αβ,使得length[a]=length[β],同樣借助一個臨時變量temp可實現向量a和β的交換,可得到第一次迭代之后的向量為βαa,接下來在對βα向量執行同樣地交換,執行一系列交換之后最終得到向量ba,而遞歸最終到達不動點(fix-point)的條件即為所要交換的兩個向量長度相等,即移位值為0。實際就是將原問題分解為一系列性質類似的子問題,利用分治的思想逐個擊破,最終達到整體交換的目標。
以上方法的偽碼實現為:
/*LOOPSHIFT(V,i) --recurrence version*/
//RECSHIFT(V, i, low, high) /*low:lower_bound high:higher_bound*/
if low=high || high<i /*i is a fix value*/
then return
if i-low>high-i+1 /*select a min value as the count of reversion*/
then revcnt←high-i+1
flag←1 /*set the flag value low bound increase*/
else revcnt←i-low
for j←0 to revcnt-1 /*swap the elem in the vector i times*/
do temp←V[low+j]
V[low+j]←V[high+1+j-revcnt]
V[high+1+j-revcnt]←temp
if flag=1
then low←low+revcnt
else high←high-revcnt
RECSHIFT(V,i,low,high) /*call itself*/
第三種方法(求逆法):令V=ab(其中a為要移位的個數),①對向量V中的前a個元素做求逆操作得到V'=a'b;②對向量V中的接下來的b個元素做求逆操作得到V''=a'b';③對整個向量V做求逆操作得到V'''=(a'b')'=ba。(同階方陣A,B有(AB)'=B'A')為了驗證該操作是否可行,以文章開始處所舉的例子(12345循環移動2個位置)進行求逆操作:12345→(①)21345→(②)21543→(③)34512,結果成立,說明該操作可行。而求逆操作中所包含的思想其實很簡單:我們在觀察一個字符串的時候往往是從左往右看的,而要循環移動其中i位,實際是將這i個字符放在整個串的末尾。而如果我們從右往左看呢?我們發現其實原本在字符串中的長度為i的子串到了整個串的末尾(即54321),我們發現兩個子串的長度換好了,但是每個子串是逆序排列的,這個時候對兩個子串各做一次求逆操作不就得出了最終的結果了嗎?這種方法所帶來的思考是:實際解決一個問題的時候,如果發現考慮的思路遇到較大阻礙,換個視角看問題往往能有意想不到的效果。
以上方法的偽碼實現為:
/*LOOPSHIFT(V,i) --reverse version*/ //REVERSE(V,i,high) /*high=high_bound*/ REVERSE(V,0,i-1) REVERSE(V,i,high) REVERSE(V,0,high) //-------------------------------------------------- REVERSE(V,low,high) /*function body*/ for j←0 to ((high-low+1)/2)-1 do temp←V[low+j] V[low+j]←V[high-j] V[high-j]←temp
ps:對于第三種方法,著名計算機科學家,unix以及C語言前身B語言的設計者Ken•Thompson在編輯器中使用這種求逆代碼時就主張將該代碼作為一種常識。
至此三種方法都介紹完了,細心的讀者也許發現前兩種方法只進行了n次交換操作,而第三種方法進行了2n次操作,因此第三種方法的性能從運行時間的角度來看應該是三種方法中最差的,理論上是如此,多進行操作的算法往往耗時也越長,但實際呢?我們不妨做個試驗來驗證一下,為了更加真實的模擬現實,n和i的取值分別如下:
n=10000000,i={21,22,…,100},分別對移位個數在[21,100]之間進行總運行時間的測量,測試代碼如下(具備可移植性,在win/linux上均可運行,其中win_xp和linux/ubuntu在本機上測試成功得出相應數據,win_7下的版本在同學的系統上運行得出相應數據):
//#define __LINUX__
#define __WINDOWS__
#include <stdio.h>
#ifdef __WINDOWS__
#include <memory.h>
#include <Windows.h>
#endif
#ifdef __LINUX__
#include <string.h>
#include <sys/time.h>
#include <unistd.h>
#endif
#define cntoffun 3
#define cntofi 80
#define start 20
#ifdef __WINDOWS__
#define mintomillsec (60*1000)
#define sectomillsec 1000
#endif
#ifdef __LINUX__
#define sectomicrosec (1e6)
#define microsectomillisec (1e-3)
#define startp 0
#define endp 1
#endif
/*i from 21 to 100*/
#define v_length 10000000
char vec[v_length];
int gcd(int n, int i);
void swap(char *a,char *b);
void loopshift_gcd(char v[],int i,int high);
void recshift(char v[],int i,int low,int high);
void reverse(char v[],int low,int high);
void reverseshift(char v[],int i,int high);
typedef int DWORD;
int main()
{
#ifdef __WINDOWS__
SYSTEMTIME tm;
#endif
#ifdef __LINUX__
struct timeval tv[2];
#endif
char colofline[]="yrb";
DWORD s_millsec,e_millsec;
FILE *fp;
int i,j;
size_t timearray[cntoffun][cntofi];
memset(vec,0,sizeof(vec));
memset(timearray,0,sizeof(timearray));
#ifdef __WINDOWS__
fp=fopen("F:\\gettimeofrp.m","w");
#endif
#ifdef __LINUX__
fp=fopen("/home/raine/Desktop/gettimeofrp.m","w");
#endif
for(j=0;j<cntoffun;j++)
{
for(i=start+1;i<=(start+cntofi);i++)
{
printf("func[%d]\tcount_of_shift[%d]\t",j,i);
#ifdef __WINDOWS__
GetLocalTime(&tm);
s_millsec=tm.wMinute*mintomillsec+tm.wSecond*sectomillsec+ \
tm.wMilliseconds;
#endif
#ifdef __LINUX__
gettimeofday(&tv[startp],NULL);
#endif
if (j==0)
loopshift_gcd(vec,i,v_length-1);
else if (j==1)
recshift(vec,i,0,v_length-1);
else
reverseshift(vec,i,v_length-1);
#ifdef __WINDOWS__
GetLocalTime(&tm);
e_millsec=tm.wMinute*mintomillsec+tm.wSecond*sectomillsec+ \
tm.wMilliseconds;
timearray[j][i-start-1] = e_millsec - s_millsec;
#endif
#ifdef __LINUX__
gettimeofday(&tv[endp],NULL);
timearray[j][i-start-1] = ((tv[endp].tv_sec-tv[startp].tv_sec)*sectomicrosec+\
(tv[endp].tv_usec-tv[startp].tv_usec))*microsectomillisec;
#endif
printf("use time %d\n",timearray[j][i-start-1]);
}
}
/*matlab code*/
fprintf(fp,"clear;\nclc;\nord_x=[...\n");
for(i=start+1;i<=(start+cntofi);i++)
{
fprintf(fp,"%d ",i);
if(i%10==0) fprintf(fp,"...\n");
}
fprintf(fp,"];\n\n");
for(i=0;i<cntoffun;i++)
{
fprintf(fp,"ord_yfunc%d=[...\n",i+1);
for(j=0;j<cntofi;j++)
{
fprintf(fp,"%d ",timearray[i][j]);
if ((j+1)%10 == 0) fprintf(fp,"...\n");
}
fprintf(fp,"];\n\n");
}
fprintf(fp,"title('performance of three function');\n");
fprintf(fp,"xlabel('x=[21:100]');\n");
fprintf(fp,"ylabel('the time three function use(millisecond)');\n");
fprintf(fp,"hold on;\n");
for(i=0;i<cntoffun;i++)
fprintf(fp,"plot(ord_x,ord_yfunc%d,'%c*-');\n",i+1,colofline[i]);
fprintf(fp,"legend('func1'");
for(i=1;i<cntoffun;i++)
fprintf(fp,",'func%d'",i+1);
fprintf(fp,");");
fclose(fp);
printf("\nhave been finished,press any key to quit ^ ^\n");
#ifdef __WINDOWS__
system("pause");
#endif
}
void swap(char *a,char *b)
{
char temp=*a;*a=*b;*b=temp;
}
int gcd(int n,int i) /*n:length[v], i:shift times, n>=i*/
{
int temp=i;
while(n%i != 0)
{
temp = n%i;
n=i; i=temp;
}
return temp;
}
void loopshift_gcd(char v[],int i,int high)
{
size_t length = gcd(high+1,i);
size_t cntofelem = ((high+1)/length)-1;
int cnt, j, k;
char temp;
for(cnt=0;cnt<length;cnt++)
{
temp=v[cnt];
k=i;
for(j=1;j<=cntofelem;j++)
{
v[(k-i)%(high+1)] = v[k%(high+1)];
k+=i;
}
v[(k-i)%(high+1)]=temp;
}
}
void recshift(char v[],int i,int low,int high)
{
int revcnt,j,temp=0;
if(low == high || high<i) return;
if (i-low>high-i+1)
revcnt=high-i+1,temp=1;
else
revcnt=i-low;
for(j=0;j<=revcnt-1;j++)
swap(&v[low+j],&v[high+1+j-revcnt]);
if(temp == 1)
low+=revcnt;
else
high-=revcnt;
recshift(v,i,low,high);
}
void reverse(char v[],int low,int high)
{
int j;
for(j=0;j<(high-low+1)/2;j++)
swap(&v[low+j],&v[high-j]);
}
void reverseshift(char v[],int i,int high)
{
reverse(v,0,i-1);
reverse(v,i,high);
reverse(v,0,high);
}
結果運行之后所得到的M文件(matlab)如下(只展示了xp下所得出的版本):
%win_xp version
clear;
clc;
ord_x=[...
21 22 23 24 25 26 27 28 29 30 ...
31 32 33 34 35 36 37 38 39 40 ...
41 42 43 44 45 46 47 48 49 50 ...
51 52 53 54 55 56 57 58 59 60 ...
61 62 63 64 65 66 67 68 69 70 ...
71 72 73 74 75 76 77 78 79 80 ...
81 82 83 84 85 86 87 88 89 90 ...
91 92 93 94 95 96 97 98 99 100 ...
];
ord_yfunc1=[...
187 157 156 141 156 156 172 187 172 187 ...
204 187 203 219 203 219 219 250 234 234 ...
250 250 266 266 265 281 266 297 281 297 ...
313 312 313 328 312 344 359 360 359 359 ...
375 360 375 375 375 390 391 391 390 391 ...
391 406 390 407 422 406 406 391 406 406 ...
391 422 407 421 422 469 469 422 484 484 ...
422 407 437 422 422 437 453 485 500 453 ...
];
ord_yfunc2=[...
16 15 16 15 16 16 15 16 16 15 ...
16 31 16 15 0 0 0 0 31 0 ...
16 16 15 16 16 15 16 15 16 16 ...
15 16 16 15 16 15 16 16 15 16 ...
16 15 16 31 16 15 16 15 16 15 ...
32 15 16 16 15 15 16 16 15 16 ...
15 16 15 16 16 15 16 16 15 15 ...
16 16 15 16 16 15 16 15 16 16 ...
];
ord_yfunc3=[...
16 16 15 16 15 16 16 15 16 16 ...
15 15 16 16 15 16 16 15 16 15 ...
32 15 16 16 15 16 15 16 15 16 ...
16 15 16 15 16 16 15 16 16 31 ...
15 16 16 15 16 16 15 16 15 16 ...
31 16 16 15 16 15 16 15 16 16 ...
15 16 16 16 15 16 16 15 16 31 ...
16 15 16 16 15 16 15 16 16 31 ...
];
title('performance of three function(Win xp)');
xlabel('x=[21:100]');
ylabel('the time three function use(millisecond)');
hold on;
plot(ord_x,ord_yfunc1,'y*-');
plot(ord_x,ord_yfunc2,'r*-');
plot(ord_x,ord_yfunc3,'b*-');
legend('func1','func2','func3');
執行所得圖形化表示如下(順序分別為win_xp,win_7,GUN/Linux_Ubuntu):
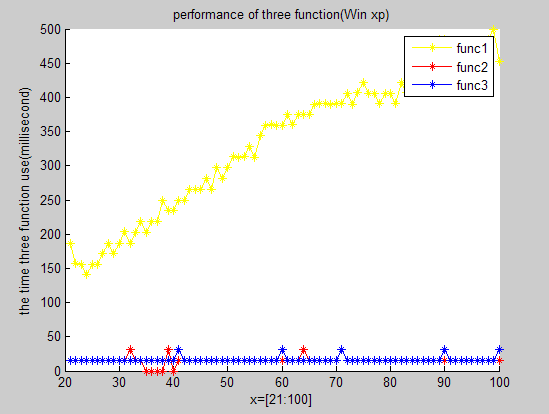
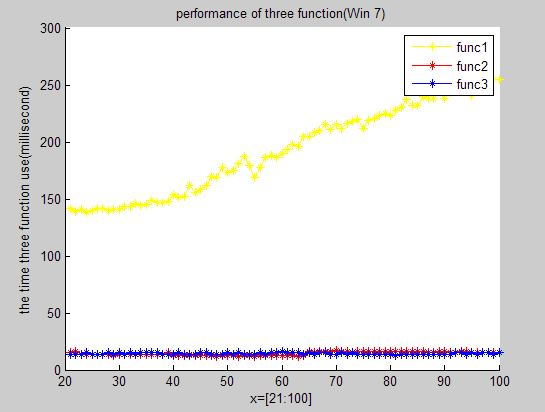
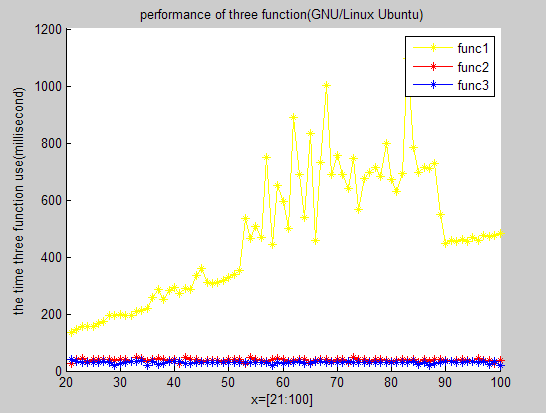
由于winxp版本的運行時間是在真實硬件環境中得出的,而win7版本則在同學的機器上得出,linux版本的則是用軟件模擬出來的硬件環境,因此進行橫向比較往往沒有多大意義。而進行縱向比較可得出的結論如下:
①由圖示可知,算法一(即求模算法)是性能最差的,算法二和算法三性能相當。這與我們當初預測的算法的操作次數越少則運行時間越短存在悖逆,想想這是為什么?
②各算法實際運行過程中往往還需要考慮操作系統的調度以及進程切換的影響。由windows兩個版本的圖示可知,該算法的運行相對算法中需要移位的個數的增量相對比較穩定。因此,從某種意義上可以看出windows的調度子系統相對比較穩定。
對于結論①中提出的問題,聰明的你是否已經有了自己的答案?沒錯,那就是傳說中的存儲器層次結構的老朋友:局部性。
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。