您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
怎么在python中使用opencv實現一個SURF算法?針對這個問題,這篇文章詳細介紹了相對應的分析和解答,希望可以幫助更多想解決這個問題的小伙伴找到更簡單易行的方法。
目標:
SURF算法基礎
opencv總SURF算法的使用
原理:
上節課使用了SIFT算法,當時這種算法效率不高,需要更快速的算法。在06年有人提出了SURF算法“加速穩定特征”,從名字上來看,他是SIFT算法的加速版本。
(原文)
在SIFT算法當中使用高斯差分方程(Difference of Gaussian)對高斯拉普拉斯方程( Laplacian of Gaussian)進行近似。然而,SURF使用盒子濾波器進行近似,下面的圖片顯示了這種近似的方法。在進行卷積計算的時候可以利用積分圖像,這是使用盒子形濾波器的一個優點,即計算某個窗口中的像素和的時候,計算量大小,也就是時間復雜度不受到窗口大小的影響。而且,這種運算可以在不用的尺度空間當中實現。
SURF算法計算關鍵點的尺度和位置信息使用Hessian矩陣實現。
(解釋)
文中的高斯拉普拉斯方程(算子)是檢測圖像中斑點的一種十分常用的方法。以一維高斯函數來檢測一維信號中的斑點為例。有一維信號f,高斯函數的一階導數
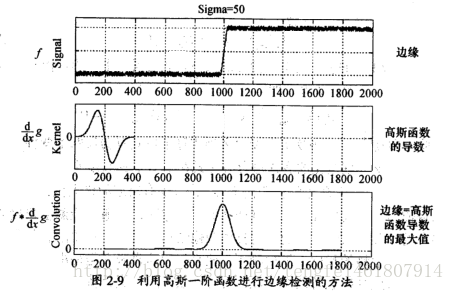
上面圖片是在一維情況下,使用高斯函數的一階導數的情況,另一種方法是使用高斯函數的二階導數與信號進行卷積,高斯函數的二階導數也叫做拉普拉斯變換。
但是,在一維信號斑點檢測的實際情況當中,一個斑點可以考慮成是兩個相鄰的跳突組成,如下圖。
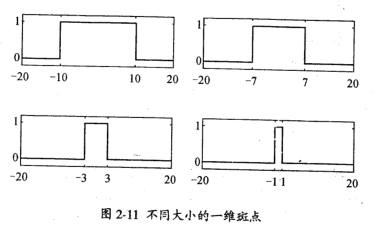
類似于在圖像當中,一個輪胎可以當成一個斑點,一個蒼蠅也可以當成一個斑點。但是在使用高斯函數的二階導數來檢測斑點的時候,使用不同的高斯核(就是方差)運算不同大小的斑點時,計算出來的極值,即響應值會出現衰減。
此時,需要將高斯函數的二階導數進行正規化,去除方差值不同導致響應值出現的衰減。
以上,是一維高斯函數檢測一維信號的原理。二維的圖像信號,使用二維高斯函數來檢測斑點原理基本相同,此處的二維高斯函數的二階導數,就叫做高斯拉普拉斯算子也就是LOG,通過改變不同的方差值,可以檢測不同尺寸的二維斑點,如圖。
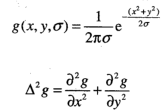
文中的高斯差分方程是SIFT算法當中,發明者想要利用兩個相鄰高斯尺度空間的圖像相減來得到一個LOG的近似,因為這樣做可以節省時間,而且可以控制精度變化,類似于高等數學當中泰勒公式那玩意-_- 。關于SIFT原理可以看上一篇博客
文中提到的積分圖像實際上原理非常簡單,類似遞推方程。積分圖像的目的是想建立一個函數,能夠快速得到一個矩形圖像區域當中所有像素值的和是多少。那么,設
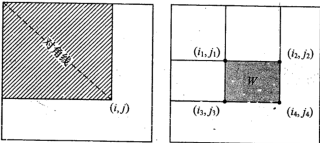
如何求得
文中提到的Hessian矩陣,學過數學分析、最優化、機器學習之類的人肯定對這玩意非常熟悉,實際上黑塞矩陣就是一個多元函數的二階偏導數構成的方陣,它的行列式值(Determinant of Hessian )可以反映的局部結構信息,簡稱DOH。與LOG類似,DOH可以使用不同方差生成高斯函數對各個元的二階偏導模板,以此來對圖像進行卷積運算。 同樣,DOH也會在卷積后的函數中,得到對圖像信號斑點極值的響應。如圖
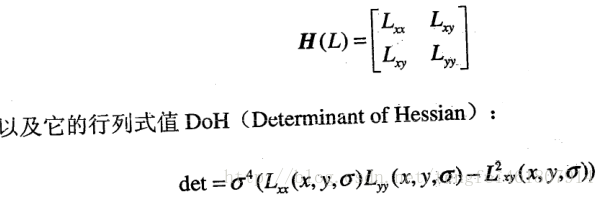
在SURF算法當中,黑塞矩陣中的L,即為二維高斯函數與圖像的卷積,求得黑塞矩陣后,會得到如圖。
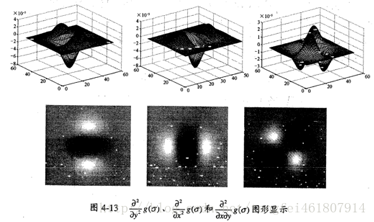
將上面得到的模板與圖像的卷積轉換為盒子濾波器,這里使用原文中的圖像,如圖。
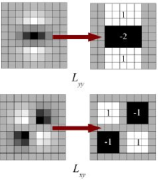
得到三個不同的盒子濾波器以后,對其進行近似和簡化操作,并用其表示圖像中某點的斑點響應值,遍歷圖像當中的所有像素,就得到了在某一尺度下斑點檢測的響應圖像。然后,利用不同的模板尺寸,獲取多尺度斑點響應金字塔,在金字塔中搜索極值點,下面的操作就和SIFT算法類似了。
(原文)
為了給找到的特征點賦予方向,以特征點為中心,6s為半徑獲取水平和垂直小波響應運算結果,這里s是特征點尺度,同時使用高斯加權的方法。然后,他們會被繪制在如下圖當中。其中,特征點的主方向估計運算是有一個弧度為60的扇形窗口,在滑動的過程中不斷計算其中的響應值之和。有趣的是,小波響應值在任意尺度下使用積分圖像很容易被獲取。但是在多數情況下,旋轉不變性不是必須的,可以代碼當中將這一步取消,這樣還能夠提高算法計算速度,而且在+-15度的情況也保持穩定,此時該方法稱作 U-SURF。用戶可以設置upright參數,當參數為0計算方向,參數為1不計算方向。
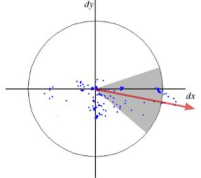
對于特征點描述的建立,SURF再一次使用Haar小波響應,同時使用積分圖像使操作變得簡單。在一個矩形區域當中,以特征點為中心,劃取周圍20s×20s區域的大小,以特征點為原點,主方向為橫軸,分成四個子區域,每個子區域使用2s的Haar小波響應,對于每個子區域,獲取一個向量,記錄垂直、水平方向上的小波響應值,如圖。
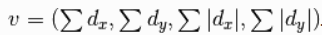
這個特征描述符的長度使64,降低維度可以加速計算,又可以區分特征。為了更好的區分特征點,SURF還使用了長度為128特征描述符。當dy小于0或者大于0時,計算dx或|dx|的和。同樣,根據dx的符號計算不同的dy和。因此能夠獲得雙倍的特征。計算復雜度也不會增加。opencv當中的extended參數為0或1時分別對應64和128的特征。
另外一個重要的改善是對潛在的興趣點使用了拉普拉斯算子符號(黑塞矩陣的跡)。由于之前的計算已經完成對黑塞矩陣的構造,所以這步不會增加復雜度。
拉普拉斯符號在不同明暗背景下區分不同亮度的斑點,在匹配階段,我們只需要比較擁有相同對比度的特征是否匹配即可,這樣加快了計算速度,如圖。
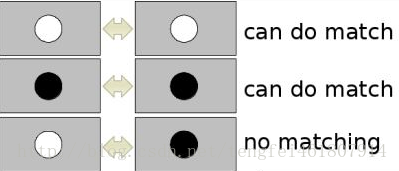
SURF算法的速度是SIFT速度的3倍,善于處理模糊和旋轉的圖像,但是不善于處理視角變化和關照變化。
(解釋)
文中的小波響應運算,全稱是haar小波運算。這里使用haar小波目的是為了獲取圖像梯度,使用之前計算好的圖像積分結果,這樣能夠提高計算速度。與SIFT算法類似,在對每個特征點獲取主方向時,使用原文中提到的一個π/3大小的扇形窗口,同時以0.2弧度為步長旋轉滑動此窗口,在每個窗口當中對的haar響應值的水平方向,垂直方向進行累加。由于時使用一個圓形區域,轉換成類似極坐標矢量的方式來表示,每個窗口中的結果
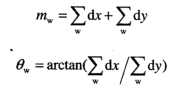
主方向最大Haar響應值累加對應的方向。其中,如果除了主方向,還有其它方向的響應累加值較大,算法當中還會額外添加一個特征點,并賦予另外一個次大方向。
文中建立的特征描述符顧名思義,就是描述一個特征點的一組向量,里面唯一確定了一個特征。SURF獲取主方向后,需要獲取特征點描述子。以特征點為原點,主方向為橫軸建立一個二維坐標系,區域大小是20s×20s,分成是個之塊,每個子塊利用2s的haar模板進行響應計算。然后統計
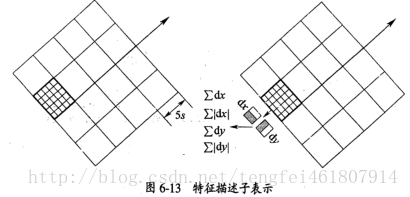
又4×4個子塊,每個子塊里面記錄四個值,所以描述子一共又4×4×4=64個特征。
最后將沿著主方向的小波響應值扭轉過來,原理就是簡單的旋轉矩陣。
代碼部分
opencv里面提供的SURF算法和SIFT差不多,這兩個玩意都是受到版權保護的,如果你是用pip 一條命令安裝的opencv,那么恭喜你用不了SURF和SIFT算法,印象中只有2.4.9版本的opencv庫才可以使用。
不過,辦法還是有的,再控制臺當中輸入pip install opencv-contrib-python 就可以用了。
如果還是無法安裝,可以直接網站早opencv-contrib-python的輪子,然后放到對應的文件下安裝就行了。
我的版本是opencv 3.2,和教程文檔中的使用方法不同。
詳細參數可以自己去查一查,一查一個準的
https://docs.opencv.org/master/d5/df7/classcv_1_1xfeatures2d_1_1SURF.html
import cv2
import numpy as np
img = cv2.imread('feng.jpg')
#參數為hessian矩陣的閾值
surf = cv2.xfeatures2d.SURF_create(400)
#找到關鍵點和描述符
key_query,desc_query = surf.detectAndCompute(img,None)
#把特征點標記到圖片上
img=cv2.drawKeypoints(img,key_query,img)
cv2.imshow('sp',img)
cv2.waitKey(0)
鳳的嘴上特征點占了這么多,辨識度還是蠻高的~ -_-|||
下面是設置方向,和輸出一些值的方法
import cv2
import numpy as np
img = cv2.imread('feng.jpg')
#參數為hessian矩陣的閾值
surf = cv2.xfeatures2d.SURF_create(4000)
#設置是否要檢測方向
surf.setUpright(True)
#輸出設置值
print(surf.getUpright())
#找到關鍵點和描述符
key_query,desc_query = surf.detectAndCompute(img,None)
img=cv2.drawKeypoints(img,key_query,img)
#輸出描述符的個數
print(surf.descriptorSize())
cv2.imshow('sp',img)
cv2.waitKey(0)關于怎么在python中使用opencv實現一個SURF算法問題的解答就分享到這里了,希望以上內容可以對大家有一定的幫助,如果你還有很多疑惑沒有解開,可以關注億速云行業資訊頻道了解更多相關知識。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。