溫馨提示×
您好,登錄后才能下訂單哦!
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好,登錄后才能下訂單哦!
正態分布應用最廣泛的連續概率分布,其特征是“鐘”形曲線。這種分布的概率密度函數為:
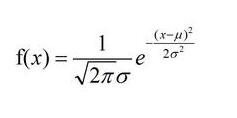
其中,μ為均值,σ為標準差。
求正態分布曲線下面積有3σ原則:
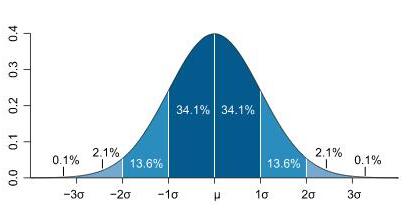
正態曲線下,橫軸區間(μ-σ,μ+σ)內的面積為68.268949%,橫軸區間(μ-1.96σ,μ+1.96σ)內的面積為95.449974%,橫軸區間(μ-2.58σ,μ+2.58σ)內的面積為99.730020%。
求任意區間內曲線下的面積,通常可以引用scipy包中的相關函數
norm函數生成一個給定均值和標準差的正態分布,cdf(x)表示-∞到x的概率
例:(2,1)正態分布下 2-3曲線下的面積
>>> import scipy.stats >>> scipy.stats.norm(2,1).cdf(3)-0.5 0.34134474606854293
由于有時候不便于引用scipy包,自編這一函數也很簡單
求積分函數參考:復化梯形求積分
cdfd(a,b,u,o)
a,b 為區間起始范圍,u,o分別為正態分布的均值和標準差。
import math def pdf(x): return math.exp(-(x) ** 2 / (2)) / (math.sqrt(2 * math.pi)) def sum_fun_xk(xk, func): return sum([func(each) for each in xk]) def integral(a, b, n, func): h = (b - a)/float(n) xk = [a + i*h for i in range(1, n)] return h/2 * (func(a) + 2 * sum_fun_xk(xk, func) + func(b)) def cdfd(a,b,u,o): return integral((a-u)/o,(b-u)/o,10000,pdf) cdfd(2,3,2,1) Out: 0.3413399854638336
以上這篇Python求正態分布曲線下面積實例就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。