python實現差分隱私Laplace機制的方法

這篇文章主要介紹了python實現差分隱私Laplace機制的方法，具有一定借鑒價值，感興趣的朋友可以參考下，希望大家閱讀完這篇文章之后大有收獲，下面讓小編帶著大家一起了解一下。

Laplace分布定義：

下面先給出Laplace分布實現代碼：

import matplotlib.pyplot as plt
import numpy as np
 
def laplace_function(x,beta):
 result = (1/(2*beta)) * np.e**(-1*(np.abs(x)/beta))
 return result
#在-5到5之間等間隔的取10000個數
x = np.linspace(-5,5,10000)
y1 = [laplace_function(x_,0.5) for x_ in x]
y2 = [laplace_function(x_,1) for x_ in x]
y3 = [laplace_function(x_,2) for x_ in x]
 
 
plt.plot(x,y1,color='r',label='beta:0.5')
plt.plot(x,y2,color='g',label='beta:1')
plt.plot(x,y3,color='b',label='beta:2')
plt.title("Laplace distribution")
plt.legend()
plt.show()

效果圖如下：

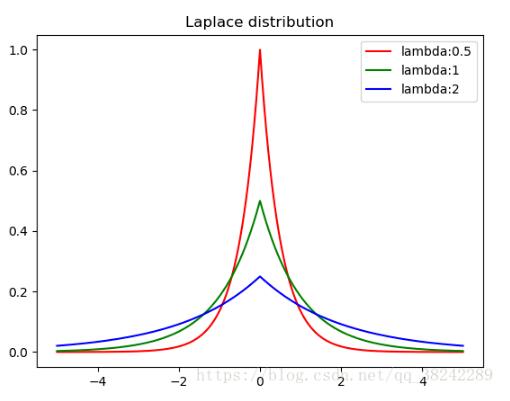
接下來給出Laplace機制實現：

Laplace機制，即在操作函數結果中加入服從Laplace分布的噪聲。

Laplace概率密度函數Lap(x|b)=1/2b exp(-|x|/b)正比于exp(-|x|/b)。

import numpy as np
 
def noisyCount(sensitivety,epsilon):
 beta = sensitivety/epsilon
 u1 = np.random.random()
 u2 = np.random.random()
 if u1 <= 0.5:
  n_value = -beta*np.log(1.-u2)
 else:
  n_value = beta*np.log(u2)
 print(n_value)
 return n_value
 
def laplace_mech(data,sensitivety,epsilon):
 for i in range(len(data)):
  data[i] += noisyCount(sensitivety,epsilon)
 return data
 
if __name__ =='__main__':
 x = [1.,1.,0.]
 sensitivety = 1
 epsilon = 1
 data = laplace_mech(x,sensitivety,epsilon)
 for j in data:
  print(j)

感謝你能夠認真閱讀完這篇文章，希望小編分享的“python實現差分隱私Laplace機制的方法”這篇文章對大家有幫助，同時也希望大家多多支持億速云，關注億速云行業資訊頻道，更多相關知識等著你來學習!