您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
建立完回歸模型后,還需要驗證咱們建立的模型是否合適,換句話說,就是咱們建立的模型是否真的能代表現有的因變量與自變量關系,這個驗證標準一般就選用擬合優度。
擬合優度是指回歸方程對觀測值的擬合程度。度量擬合優度的統計量是判定系數R^2。R^2的取值范圍是[0,1]。R^2的值越接近1,說明回歸方程對觀測值的擬合程度越好;反之,R^2的值越接近0,說明回歸方程對觀測值的擬合程度越差。
擬合優度問題目前還沒有找到統一的標準說大于多少就代表模型準確,一般默認大于0.8即可
擬合優度的公式:R^2 = 1 - RSS/TSS
注: RSS 離差平方和 ; TSS 總體平方和
理解擬合優度的公式前,需要先了解清楚幾個概念:總體平方和、離差平方和、回歸平方和。
一、總體平方和、離差平方和、回歸平方和
回歸平方和 ESS,殘差平方和 RSS,總體平方和 TSS
TSS(Total Sum of Squares)表示實際值與期望值的離差平方和,代表變量的總變動程度
ESS(Explained Sum of Squares)表示預測值與期望值的離差平方和,代表預測模型擁有的變量變動程度
RSS(Residual Sum of Squares)表示實際值與預測值的離差平方和,代表變量的未知變動程度
各個平方和的計算公式如下:
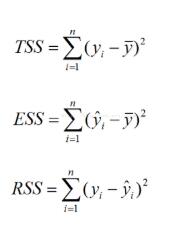
二、擬合優度
接上一節內容可知,我們拿實際值與期望值的離差平方和作為整體變量的總變動程度,這個變動程度就是我們建模型的目的,我們建立模型就是為了模擬這個變動程度。
建立模型后,整體變量的總變動程度(TSS)可以劃分為兩部分:模型模擬的變動程度(ESS)和未知的變動程度(RSS)
通常來說,預測模型擁有的變量變動程度在總變動程度中的占比越高,代表模型越準確,當RSS=0時,表示模型能完全模擬變量的總變動。
回到文章開頭的擬合優度公式:R^2 = 1 - RSS/TSS 。是不是很好理解了!
假設R^2 = 0.8,意味著咱們建立的模型擁有的變動程度能模擬80%的總變動程度,剩下20%為未知變動。
三、例子
對于學生而言,現在要探索一下學生的學習成績與單一的學習時間是否有關系,給出兩組數據如下:
'學習時間':[0.50,0.75,1.00,1.25,1.50,1.75,1.75, 2.00,2.25,2.50,2.75,3.00,3.25,3.50,4.00,4.25,4.50,4.75,5.00,5.50],
'分數':[10,22,13,43,20,22,33,50,62,48,55,75,62,73,81,76,64,82,90,93]
常識理解,學習時間越長,分數一般都會越高,兩者是正比關系,因為就一個自變量,直接用sklearn,算出截距和斜率即可
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pandas import DataFrame,Series
from sklearn.cross_validation import train_test_split
from sklearn.linear_model import LinearRegression
#創建數據集
examDict = {'學習時間':[0.50,0.75,1.00,1.25,1.50,1.75,1.75,
2.00,2.25,2.50,2.75,3.00,3.25,3.50,4.00,4.25,4.50,4.75,5.00,5.50],
'分數':[10,22,13,43,20,22,33,50,62,
48,55,75,62,73,81,76,64,82,90,93]}
#轉換為DataFrame的數據格式
examDf = DataFrame(examDict)
#examDf
#繪制散點圖
plt.scatter(examDf.分數,examDf.學習時間,color = 'b',label = "Exam Data")
#添加圖的標簽(x軸,y軸)
plt.xlabel("Hours")
plt.ylabel("Score")
#顯示圖像
plt.show()
#將原數據集拆分訓練集和測試集
exam_X = examDf.學習時間
exam_Y = examDf.分數
X_train,X_test,Y_train,Y_test = train_test_split(exam_X,exam_Y,train_size=0.8)
#X_train為訓練數據標簽,X_test為測試數據標簽,exam_X為樣本特征,exam_y為樣本標簽,train_size 訓練數據占比
print("原始數據特征:",exam_X.shape,
",訓練數據特征:",X_train.shape,
",測試數據特征:",X_test.shape)
print("原始數據標簽:",exam_Y.shape,
",訓練數據標簽:",Y_train.shape,
",測試數據標簽:",Y_test.shape)
model = LinearRegression()
#對于模型錯誤我們需要把我們的訓練集進行reshape操作來達到函數所需要的要求
# model.fit(X_train,Y_train)
#reshape如果行數=-1的話可以使我們的數組所改的列數自動按照數組的大小形成新的數組
#因為model需要二維的數組來進行擬合但是這里只有一個特征所以需要reshape來轉換為二維數組
X_train = X_train.values.reshape(-1,1)
X_test = X_test.values.reshape(-1,1)
model.fit(X_train,Y_train)
a = model.intercept_#截距
b = model.coef_#回歸系數
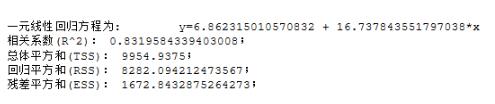
print("最佳擬合線:截距",a,",回歸系數:",b)
接下來算出擬合優度看看 ,擬合優度0.83,符合要求
# 用訓練集進行擬合優度,驗證回歸方程是否合理
def get_lr_stats(x, y, model):
message0 = '一元線性回歸方程為: '+'\ty' + '=' + str(model.intercept_)+' + ' +str(model.coef_[0]) + '*x'
from scipy import stats
n = len(x)
y_prd = model.predict(x)
Regression = sum((y_prd - np.mean(y))**2) # 回歸平方和
Residual = sum((y - y_prd)**2) # 殘差平方和
total = sum((y-np.mean(y))**2) #總體平方和
R_square = 1-Residual / total # 相關性系數R^2
message1 = ('相關系數(R^2): ' + str(R_square) + ';' + '\n'+ '總體平方和(TSS): ' + str(total) + ';' + '\n')
message2 = ('回歸平方和(RSS): ' + str(Regression) + ';' + '\n殘差平方和(ESS): ' + str(Residual) + ';' + '\n')
return print(message0 +'\n' +message1 + message2 )
get_lr_stats(X_train,Y_train,model)
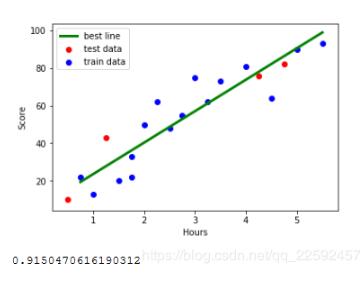
如果需要,可以把所有點和回歸直線畫出來,直觀感受一下
#訓練數據的預測值
y_train_pred = model.predict(X_train)
#繪制最佳擬合線:標簽用的是訓練數據集中的極值預測值
X_train_pred = [min(X_train),max(X_train)]
y_train_pred = [a+b*min(X_train),a+b*max(X_train)]
plt.plot(X_train_pred, y_train_pred, color='green', linewidth=3, label="best line")
#測試數據散點圖
plt.scatter(X_test, Y_test, color='red', label="test data")
plt.scatter(X_train, Y_train, color="blue", label="train data")
#添加圖標標簽
plt.legend(loc=2)
plt.xlabel("Hours")
plt.ylabel("Score")
#顯示圖像
plt.savefig("lines.jpg")
plt.show()
#計算擬合優度
score = model.score(X_test,Y_test)
print(score)
以上這篇python 線性回歸分析模型檢驗標準--擬合優度詳解就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。