您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“怎么用Python進行多元線性回歸”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!
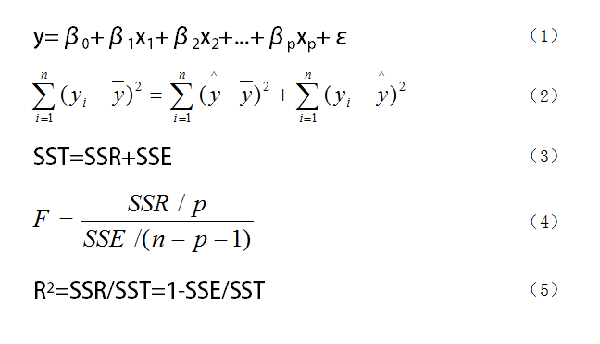
圖1. 多元回歸模型中要用到的公式
如圖1所示,我們假設隨機變量y與一般變量x1、x2、...、xp之間線性回歸模型為(1)式,式中y為因變量,x1、x2、...、xp是自變量,β1、β2、...、βp是回歸系數,β0是回歸常數。對于一個實際問題,如果我們獲得n組觀測數據(xi1,xi2,...,xip;y)(i = 1,2,...,n),則我們可以把這n組觀測數據寫成矩陣形式y=Xβ+ε。
在求出了回歸方程之后,我們往往還要對回歸方程進行顯著性檢驗。這里的顯著性檢驗主要包括三部分。第一個是F檢驗,也就是檢驗自變量x1、x2、...、xp從整體上對y是否有明顯的影響,主要用到(2)、(3)、(4)式,其中(2)和(3)式是一個式子,不過是用不同符號表示;第二個是t檢驗,是對每個自變量進行顯著性檢驗,就是看每個自變量是否對y有顯著性影響,這和前面從整體上檢驗還是有區別的;第三個是擬合優度,也就是R2,其取值在0到1之間,越接近1,表明回歸擬合的效果越好,越接近于0,則效果越差,但R只能直觀反映擬合的效果,不能代替F檢驗作為嚴格的顯著性檢驗。
上面是多元線性回歸的一個簡單介紹,其詳細原理內容較多,有興趣的讀者可以去查閱一下相關文獻,這里不再贅述,只重點講解如何用python進行分析。下面我們還是用代碼來展示一下多元線性回歸的分析過程。
這里我們用到的數據來源于2013年《中國統計年鑒》,數據以居民的消費性支出為因變量y,其他9個變量為自變量,其中x1是居民的食品花費,x2是衣著花費,x3是居住花費,x4是醫療保健花費,x5是文教娛樂花費,x6是職工平均工資,x7是地區的人均GDP,x8是地區的消費價格指數,x9是地區的失業率。在這所有變量里面,x1至x7以及y的單位是元,x9是百分數,x8沒有單位,因為其是消費價格指數。數據的總體大小為31x10,即31行、10列,大體內容如圖2所示。
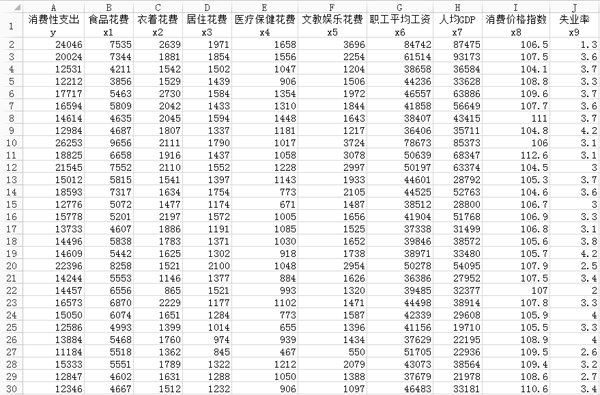
圖2. 數據集部分內容
首先還是導入需要的庫。
import numpy as np import pandas as pd import statsmodels.api as sm
接下來是數據預處理,因為原數據的列標太長,我們要處理一下,去除其中的中文,只留下英文名稱。
file = r'C:\Users\data.xlsx' data = pd.read_excel(file) data.columns = ['y', 'x1', 'x2', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x9']
然后我們就開始生成多元線性模型,代碼如下。
x = sm.add_constant(data.iloc[:,1:]) #生成自變量 y = data['y'] #生成因變量 model = sm.OLS(y, x) #生成模型 result = model.fit() #模型擬合 result.summary() #模型描述
很明顯,這里的自變量是指x1到x9這9個自變量,代碼data.iloc[:,1:]就是去掉原數據中第一列,也就是y那一列的數據,result.summary()則是生成一份結果描述,其內容如圖3所示。
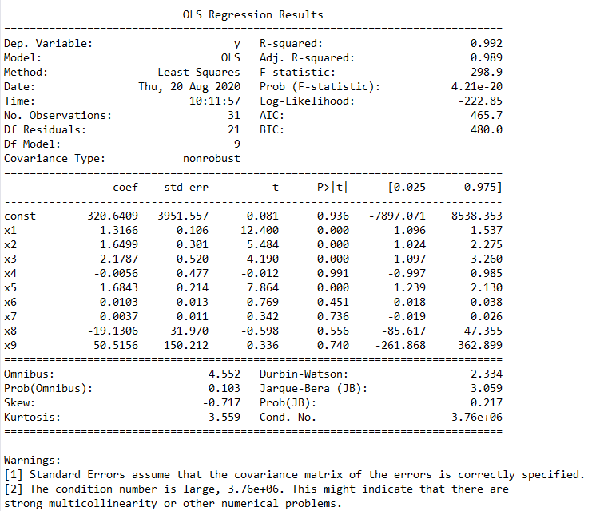
圖3. 包含所有自變量的回歸結果
在這個結果中,我們主要看“coef”、“t”和“P>|t|”這三列。coef就是前面說過的回歸系數,const這個值就是回歸常數,所以我們得到的這個回歸模型就是y = 320.640948 + 1.316588 x1 + 1.649859 x2 + 2.17866 x3 - 0.005609 x4 + 1.684283 x5 + 0.01032 x6 + 0.003655 x7 -19.130576 x8 + 50.515575 x9。而“t”和“P>|t|”這兩列是等價的,使用時選擇其中一個就行,其主要用來判斷每個自變量和y的線性顯著關系,后面我們會講到。從圖中還可以看出,Prob (F-statistic)為4.21e-20,這個值就是我們常用的P值,其接近于零,說明我們的多元線性方程是顯著的,也就是y與x1、x2、...、x9有著顯著的線性關系,而R-squared是0.992,也說明這個線性關系比較顯著。理論上,這個多元線性方程已經求出來了,而且效果還不錯,我們就可以用其進行預測了,但這里我們還是要進行更深一步的探討。前面說過,y與x1、x2、...、x9有著顯著的線性關系,這里要注意x1到x9這9個變量被看作是一個整體,y與這個整體有顯著的線性關系,但不代表y與其中的每個自變量都有顯著的線性關系,我們在這里要找出那些與y的線性關系不顯著的自變量,然后把它們剔除,只留下關系顯著的,這就是前面說過的t檢驗,t檢驗的原理內容有些復雜,有興趣的讀者可以自行查閱資料,這里不再贅述。我們可以通過圖3中“P>|t|”這一列來判斷,這一列中我們可以選定一個閾值,比如統計學常用的就是0.05、0.02或0.01,這里我們就用0.05,凡是P>|t|這列中數值大于0.05的自變量,我們都把它剔除掉,這些就是和y線性關系不顯著的自變量,所以都舍去,請注意這里指的自變量是x1到x9,不包括圖3中const這個值。但是這里有一個原則,就是一次只能剔除一個,剔除的這個往往是P值最大的那個,比如圖3中P值最大的是x4,那么就把它剔除掉,然后再用剩下的x1、x2、x3、x5、x6、x7、x8、x9來重復上述建模過程,再找出P值最大的那個自變量,把它剔除,如此重復這個過程,直到所有P值都小于等于0.05,剩下的這些自變量就是我們需要的自變量,這些自變量和y的線性關系都比較顯著,我們要用這些自變量來進行建模。
我們可以將上述過程寫成一個函數,命名為looper,代碼如下。
def looper(limit): cols = ['x1', 'x2', 'x3', 'x5', 'x6', 'x7', 'x8', 'x9'] for i in range(len(cols)): datadata1 = data[cols] x = sm.add_constant(data1) #生成自變量 y = data['y'] #生成因變量 model = sm.OLS(y, x) #生成模型 result = model.fit() #模型擬合 pvalues = result.pvalues #得到結果中所有P值 pvalues.drop('const',inplace=True) #把const取得 pmax = max(pvalues) #選出最大的P值 if pmax>limit: ind = pvalues.idxmax() #找出最大P值的index cols.remove(ind) #把這個index從cols中刪除 else: return result result = looper(0.05) result.summary()其結果如圖4所示。從結果中可以看到最后剩下的有效變量為x1、x2、x3和x5,我們得到的多元線性模型為y = -1694.6269 + 1.3642 x1 + 1.7679 x2 + 2.2894 x3 + 1.7424 x5,這個就是我們最終要用到的有效的多元線性模型。
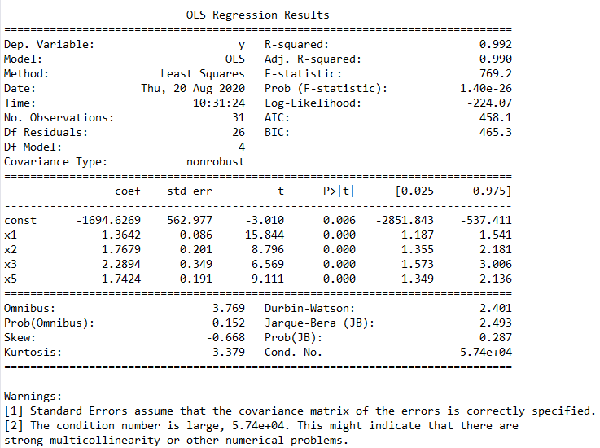
圖4. 剔除無效變量后的回歸模型
那么問題來了,前面我們得到的包含所有自變量的多元線性模型和這個剔除部分變量的模型,我們要選擇哪一個,畢竟第一個模型的整體線性效果也挺顯著,依據筆者的經驗,這個還是要看具體的項目要求。因為我們實際項目中遇到的問題都是現實生活中真實存在的例子,不再是單純的數學題了,比如本例中的x8消費價格指數和x9地區的失業率,這兩個肯定對y是有一定影響的,如果盲目剔除,可能會對最終的結果產生不良影響,所以我們還是要根據實際需求來做決定。
“怎么用Python進行多元線性回歸”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。