python如何實現logistic分類算法

小編給大家分享一下python如何實現logistic分類算法，相信大部分人都還不怎么了解，因此分享這篇文章給大家參考一下，希望大家閱讀完這篇文章后大有收獲，下面讓我們一起去了解一下吧！

最近在看吳恩達的機器學習課程，自己用python實現了其中的logistic算法，并用梯度下降獲取最優值。

logistic分類是一個二分類問題，而我們的線性回歸函數

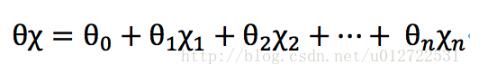
的取值在負無窮到正無窮之間，對于分類問題而言，我們希望假設函數的取值在0~1之間，因此logistic函數的假設函數需要改造一下

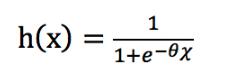
由上面的公式可以看出，0 < h(x) < 1，這樣，我們可以以1/2為分界線

cost function可以這樣定義

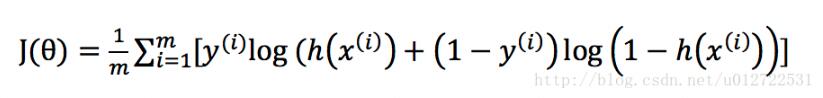
其中，m是樣本的數量，初始時θ可以隨機給定一個初始值，算出一個初始的J(θ)值，再執行梯度下降算法迭代，直到達到最優值，我們知道，迭代的公式主要是每次減少一個偏導量

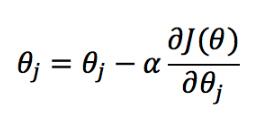
如果將J(θ)代入化簡之后，我們發現可以得到和線性回歸相同的迭代函數

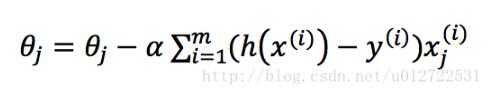
按照這個迭代函數不斷調整θ的值，直到兩次J(θ)的值差值不超過某個極小的值之后，即認為已經達到最優解，這其實只是一個相對較優的解，并不是真正的最優解。 其中，α是學習速率，學習速率越大，就能越快達到最優解，但是學習速率過大可能會讓懲罰函數最終無法收斂，整個過程python的實現如下

import math

ALPHA = 0.3
DIFF = 0.00001


def predict(theta, data):
  results = []
  for i in range(0, data.__len__()):
    temp = 0
    for j in range(1, theta.__len__()):
      temp += theta[j] * data[i][j - 1]
    temp = 1 / (1 + math.e ** (-1 * (temp + theta[0])))
    results.append(temp)
  return results


def training(training_data):
  size = training_data.__len__()
  dimension = training_data[0].__len__()
  hxs = []
  theta = []
  for i in range(0, dimension):
    theta.append(1)
  initial = 0
  for i in range(0, size):
    hx = theta[0]
    for j in range(1, dimension):
      hx += theta[j] * training_data[i][j]
    hx = 1 / (1 + math.e ** (-1 * hx))
    hxs.append(hx)
    initial += (-1 * (training_data[i][0] * math.log(hx) + (1 - training_data[i][0]) * math.log(1 - hx)))
  initial /= size
  iteration = initial
  initial = 0
  counts = 1
  while abs(iteration - initial) > DIFF:
    print("第", counts, "次迭代, diff=", abs(iteration - initial))
    initial = iteration
    gap = 0
    for j in range(0, size):
      gap += (hxs[j] - training_data[j][0])
    theta[0] = theta[0] - ALPHA * gap / size
    for i in range(1, dimension):
      gap = 0
      for j in range(0, size):
        gap += (hxs[j] - training_data[j][0]) * training_data[j][i]
      theta[i] = theta[i] - ALPHA * gap / size
      for m in range(0, size):
        hx = theta[0]
        for j in range(1, dimension):
          hx += theta[j] * training_data[i][j]
        hx = 1 / (1 + math.e ** (-1 * hx))
        hxs[i] = hx
        iteration += -1 * (training_data[i][0] * math.log(hx) + (1 - training_data[i][0]) * math.log(1 - hx))
      iteration /= size
    counts += 1
  print('training done,theta=', theta)
  return theta


if __name__ == '__main__':
  training_data = [[1, 1, 1, 1, 0, 0], [1, 1, 0, 1, 0, 0], [1, 0, 1, 0, 0, 0], [0, 0, 0, 0, 1, 1], [0, 1, 0, 0, 0, 1],
        [0, 0, 0, 0, 1, 1]]
  test_data = [[0, 1, 0, 0, 0], [0, 0, 0, 0, 1]]
  theta = training(training_data)
  res = predict(theta, test_data)
  print(res)

運行結果如下

以上是“python如何實現logistic分類算法”這篇文章的所有內容，感謝各位的閱讀！相信大家都有了一定的了解，希望分享的內容對大家有所幫助，如果還想學習更多知識，歡迎關注億速云行業資訊頻道！