您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章給大家分享的是有關原生python如何實現knn分類算法的內容。小編覺得挺實用的,因此分享給大家做個參考,一起跟隨小編過來看看吧。
一、題目要求
用原生Python實現knn分類算法。
二、題目分析
數據來源:鳶尾花數據集(見附錄Iris.txt)
數據集包含150個數據集,分為3類,分別是:Iris Setosa(山鳶尾)、Iris Versicolour(雜色鳶尾)和Iris Virginica(維吉尼亞鳶尾)。每類有50個數據,每個數據包含四個屬性,分別是:Sepal.Length(花萼長度)、Sepal.Width(花萼寬度)、Petal.Length(花瓣長度)和Petal.Width(花瓣寬度)。
將得到的數據集按照7:3的比例劃分,其中7為訓練集,3為測試集。編寫算法實現:學習訓練集的數據特征來預測測試集鳶尾花的種類,并且計算出預測的準確性。
KNN是通過測量不同特征值之間的距離進行分類。它的思路是:如果一個樣本在特征空間中的k個最相似(即特征空間中最鄰近)的樣本中的大多數屬于某一個類別,則該樣本也屬于這個類別,其中K通常是不大于20的整數。KNN算法中,所選擇的鄰居都是已經正確分類的對象。該方法在定類決策上只依據最鄰近的一個或者幾個樣本的類別來決定待分樣本所屬的類別。
三、算法設計
1)將文本文件按行分割,寫入列表datas中
def data_read(filepath): # 讀取txt文件,將讀出的內容存入datas列表中
fp = open(filepath, "r")
datas = [] # 存儲處理后的數據
lines = fp.readlines() # 讀取整個文件數據
for line in lines:
row = line.strip('\n').split(',') # 去除兩頭的換行符,按空格分割
datas.append(row)
fp.close()
return datas2)劃分數據集與測試集,將數據集的數據存入labeldata_list列表,標簽存入label_list列表,測試集數據存入text_list列表,標簽存入textlabel_list列表。
3)對得到的兩個數據集的數據和標簽列表進行處理。將labeldata_list列表數據轉換為元組labeldata_tuple,構造形入{labeldata_tuple: label_list}的字典mydict。這樣不僅可以去掉重復數據,而且可唯一的標識各個數據所對應的鳶尾花種類。
for i in range(0, 105): # 數據集按照3:7的比例劃分,其中105行為訓練集,45行為測試集
labeldata_list.append([datas[i][0], datas[i][1], datas[i][2], datas[i][3]])
label_list.append(datas[i][4])
for i in range(105, 150): # 測試集的數據
text_list.append([datas[i][0], datas[i][1], datas[i][2], datas[i][3]])
textlabel_list.append(datas[i][4])
j = 0
for i in labeldata_list:
labeldata_tuple = tuple(i)
mydict.update({labeldata_tuple: label_list[j]})
j = j + 14)計算測試集數據與各個訓練集數據之間的距離,得到distance_list列表,外層循環進行一次,都會有一個該測試數據所對應的與訓練數據最短距離。標記出該距離對應的訓練集,在一個近鄰的條件下,這個訓練集的種類,就是該測試集的種類。
在計算距離時,使用絕對距離來計算。將每個訓練集對應數據的屬性值相減后求和add,得到一個測試數據與每個樣本的距離,add的最小值就是距離最小值。
for i in range(len(text_list)):
count += 1
for j in range(len(train_list)):
add1 = abs(float(train_list[j][0]) - float(text_list[i][0])) + abs(float(train_list[j][1])
- float(text_list[i][1])) + abs(
float(train_list[j][2]) - float(text_list[i][2])) + abs(float(train_list[j][3])
- float(text_list[i][3]))
distance_list.append(add1)
if add > add1:
add = add1
index = train_list[j]
print("預測", text_list[i], "的標簽是:", mydict.get(index))5)判斷預測結果的準確性:將預測的測試數據種類與原始數據對比,若相同,則分子加一。
right = 0 # 分子
count = 0 # 分母
for i in range(len(text_list)):
count += 1
for j in range(len(train_list)):
add1 = abs(float(train_list[j][0]) - float(text_list[i][0])) + abs(float(train_list[j][1])
- float(text_list[i][1])) + abs(
float(train_list[j][2]) - float(text_list[i][2])) + abs(float(train_list[j][3])
- float(text_list[i][3]))
distance_list.append(add1)
if add > add1:
add = add1
index = train_list[j]
print("預測", text_list[i], "的標簽是:", mydict.get(index))
if mydict.get(index) == textlabel_list[i]: # 當計算出來的1個近鄰與測試集正確的標簽相同時,分子加一
right = right + 1
print('預測準確性:{:.2f}'.format(right / count))6)舉例,繪圖
以測試集7.6,3.0,6.6,2.1,Iris-virginica為例:
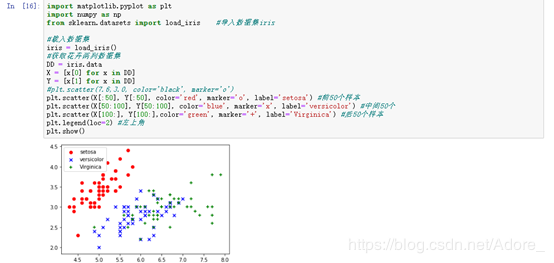
首先運用anaconda繪制出數據集的散點圖,其次,將需要測試的數據于數據集繪制在同一張圖上,在一個近鄰的前提下,距離測試數據最近的點的標簽即為測試數據的的標簽。如下圖,黑色的測試點距離紅點最近,所以,測試數據的標簽就為virginica。
import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import load_iris #導入數據集iris #載入數據集 iris = load_iris() #獲取花卉兩列數據集 DD = iris.data X = [x[0] for x in DD] Y = [x[1] for x in DD] #plt.scatter(7.6,3.0, color='black', marker='o') plt.scatter(X[:50], Y[:50], color='red', marker='o', label='setosa') #前50個樣本 plt.scatter(X[50:100], Y[50:100], color='blue', marker='x', label='versicolor') #中間50個 plt.scatter(X[100:], Y[100:],color='green', marker='+', label='Virginica') #后50個樣本 plt.legend(loc=2) #左上角 plt.show()
算法數據流圖:
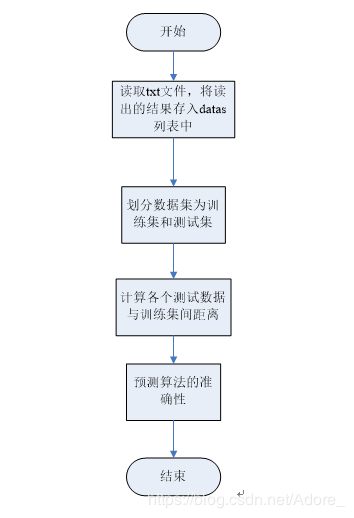
計算各個測試數據與訓練集間距離詳細流程圖:
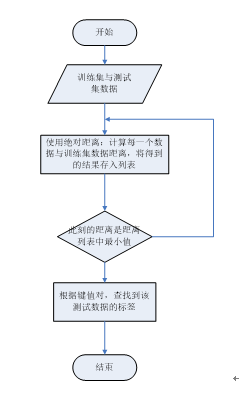
五、測試
導入數據集
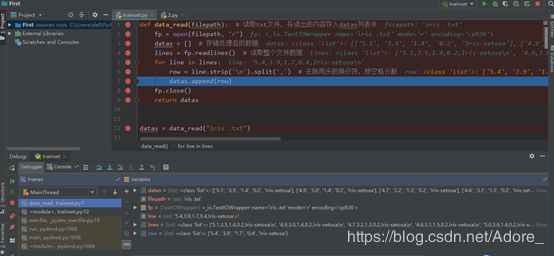
劃分數據集
訓練集:
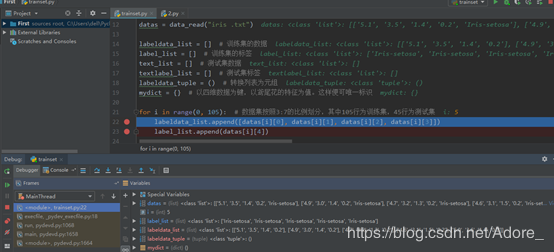
測試集:
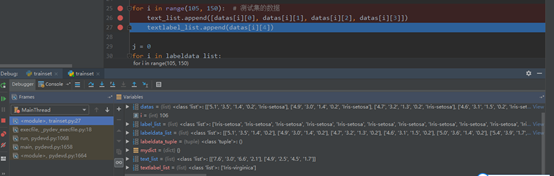
對得到的兩個數據集的數據和標簽列表進行處理
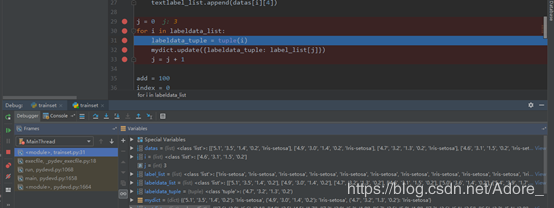
計算測試集數據與各個訓練集數據之間的距離
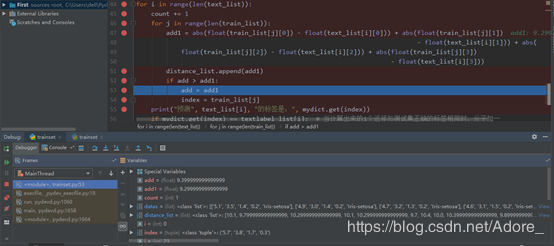
判斷預測結果的準確性
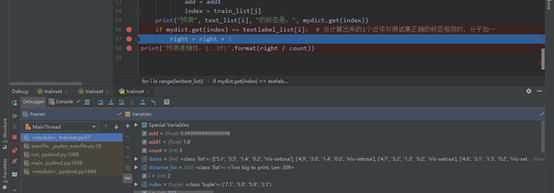
繪圖舉例
五、運行結果
1.對測試集所有數據進行預測,得到預測測試集的標簽與預測準確性
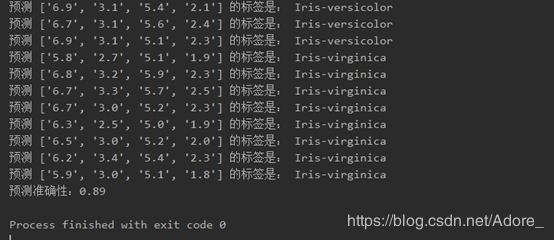
繪出散點圖:7.6,3.0,6.6,2.1,Iris-virginica作為測試集的舉例
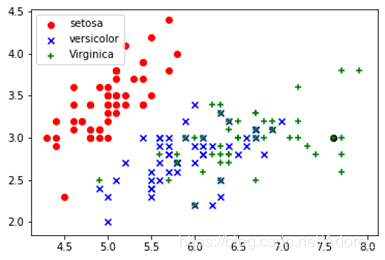
六、總結
學習了關于繪圖的函數與庫
發現在繪圖方面anaconde比pycharm要方便的多
對向量之間的距離公式進行了復習
除了這次作業中使用到的絕對距離之外,還有:
a)歐氏距離
兩個n維向量a(x11,x12,…,x1n)與 b(x21,x22,…,x2n)間的歐氏距離: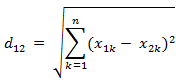
b)曼哈頓距離
兩個n維向量a(x11,x12,…,x1n)與 b(x21,x22,…,x2n)間的曼哈頓距離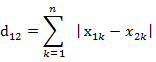
c)閔可夫斯基距離
兩個n維變量a(x11,x12,…,x1n)與 b(x21,x22,…,x2n)間的閔可夫斯基距離定義為: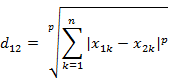
對文件的讀操作進行使用
算法缺點:用了許多for循環,會降低效率,增加算法的時間復雜度;只是一個近鄰的判斷依據
七、源代碼
def data_read(filepath): # 讀取txt文件,將讀出的內容存入datas列表中
fp = open(filepath, "r")
datas = [] # 存儲處理后的數據
lines = fp.readlines() # 讀取整個文件數據
for line in lines:
row = line.strip('\n').split(',') # 去除兩頭的換行符,按空格分割
datas.append(row)
fp.close()
return datas
datas = data_read("iris .txt")
labeldata_list = [] # 訓練集的數據
label_list = [] # 訓練集的標簽
text_list = [] # 測試集數據
textlabel_list = [] # 測試集標簽
labeldata_tuple = () # 轉換列表為元組
mydict = {} # 以四維數據為鍵,以鳶尾花的特征為值。這樣便可唯一標識
'''
劃分數據集與測試集,將數據集的數據存入labeldata_list列表,標簽存入label_list列表,
測試集數據存入text_list列表,標簽存入textlabel_list列表。
'''
for i in range(0, 105): # 數據集按照3:7的比例劃分,其中105行為訓練集,45行為測試集
labeldata_list.append([datas[i][0], datas[i][1], datas[i][2], datas[i][3]])
label_list.append(datas[i][4])
for i in range(105, 150): # 測試集的數據
text_list.append([datas[i][0], datas[i][1], datas[i][2], datas[i][3]])
textlabel_list.append(datas[i][4])
j = 0
for i in labeldata_list:
labeldata_tuple = tuple(i)
mydict.update({labeldata_tuple: label_list[j]})
j = j + 1
add = 100
index = 0
distance_list = []
train_list = []
for key, value in mydict.items():
train_list.append(key)
right = 0 # 分子
count = 0 # 分母
'''
在計算距離時,使用絕對距離來計算。
將每個訓練集對應數據的屬性值相減后求和add,
得到一個測試數據與每個樣本的距離,add的最小值就是距離最小值。
'''
for i in range(len(text_list)):
count += 1
for j in range(len(train_list)):
add1 = abs(float(train_list[j][0]) - float(text_list[i][0])) + abs(float(train_list[j][1])
- float(text_list[i][1])) + abs(
float(train_list[j][2]) - float(text_list[i][2])) + abs(float(train_list[j][3])
- float(text_list[i][3]))
distance_list.append(add1)
if add > add1:
add = add1
index = train_list[j]
print("預測", text_list[i], "的標簽是:", mydict.get(index))
if mydict.get(index) == textlabel_list[i]: # 當計算出來的1個近鄰與測試集正確的標簽相同時,分子加一
right = right + 1
print('預測準確性:{:.2f}'.format(right / count))感謝各位的閱讀!關于“原生python如何實現knn分類算法”這篇文章就分享到這里了,希望以上內容可以對大家有一定的幫助,讓大家可以學到更多知識,如果覺得文章不錯,可以把它分享出去讓更多的人看到吧!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。