您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
小編給大家分享一下web開發中連連看小游戲的制作案例,相信大部分人都還不怎么了解,因此分享這篇文章給大家參考一下,希望大家閱讀完這篇文章后大有收獲,下面讓我們一起去了解一下吧!
一. 2個物體在同一直線上,可以直接連通 (這個不需要解釋啦)

二.2個物體在同一直線上,中間有障礙物,不能直接連通 (2個轉彎)
【循環遍歷黃線中的交點,比如A,B點,再判斷藍線有沒有障礙物,若沒有,則可以連通,若有,則繼續循環查找新的A,B點】
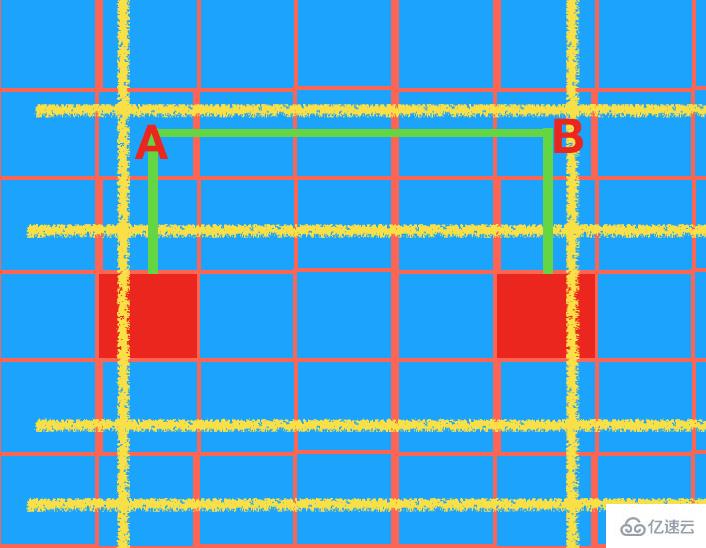
三. 2個對象不在同一直線上,一個轉彎
【2個物體分別在所在位置進行x,y軸的延伸,如下圖則交點為A,B。 只需判斷2個交點到2個物體直接是否有障礙物,若沒有,則可以連通】

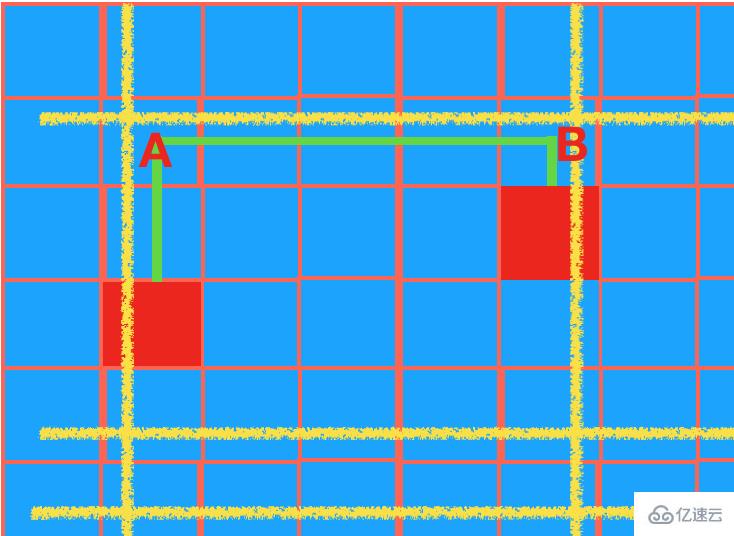
四. 2個物體不在同一直線上,連線有2個轉彎
【同二的原理,如下圖,如果A,B 2個交點到物體均沒有障礙物,則可以連通。其中A點的縱坐標和B相同】
另外一種情況,A,B 為2個物體所在x軸與中間y軸的交點,A,B的x坐標必須相同,連線如下:
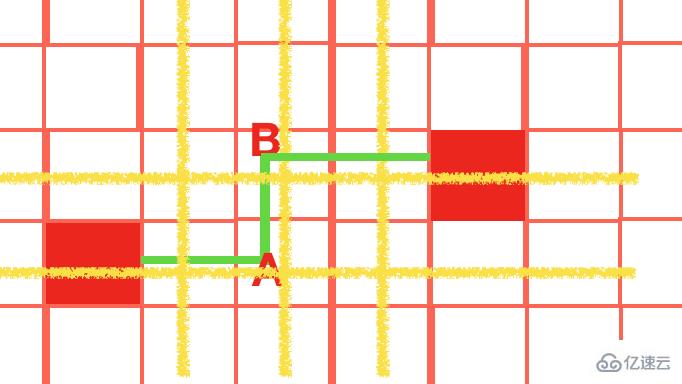
以上就是四種連線算法判斷,畫圖只畫x軸的,每一種按照同樣的原理增加y軸即可。可覆蓋所有連線判斷~
說完連線判斷的邏輯之后,寫一下整體的游戲框架,游戲基本使用原生javascript,使用createjs游戲引擎進行開發。
代碼思路:
1. 繪制游戲畫圖,確定為多少宮圖,由于是在移動端的小游戲,根據最小屏幕尺寸(iphone4 320*480),確定為7*9的宮圖。
1. 創建一個二維數組,如果某個坐標上有物體,則設為1,否則為0
2.判斷該位置是否有物體,只需要判斷對應的二維數組上值是否為1,若為1,則有物體,否則沒有。
至于畫線,消除相同物體,只要會連線邏輯,肯定就會自己繪制線條,消除物體了,所以本篇文章就只講連線判斷啦~
在判斷能否連線的時候,肯定是從最簡單的方法開始判斷,如下:
同一直線能否直線連通--->如何一點被包圍,則不通--->兩點在一條直線上,不能直線連接但是可以連通---> 不在同一直線但是可以連通
getPath: function (p1, p2) {//開始搜索前對p1,p2排序,使p2盡可能的在p1的右下方。if (p1.x > p2.x) {var t = p1;
p1 = p2;
p2 = t;
}else if (p1.x == p2.x) {if (p1.y > p2.y) {var t = p1;
p1 = p2;
p2 = t;
}
}//2點在同一直線上,可以直線連通if (this.hasLine(p1, p2).status) {return true;
}//如果兩點中任何一個點被全包圍,則不通。else if (this.isWrap(p1, p2)) {return false;
}//兩點在一條直線上,不能直線連接但是可以連通else if (this.LineLink(p1, p2)) {return true;
}//不在同一直線但是可以連通else if (this.curveLink(p1, p2)) {return true;
}
}

//判斷同一條線能否連通,x軸相同或者y軸相同hasLine: function (p1, p2) {this.path = [];//同一點if (p1.x == p2.x && p1.y == p2.y) {return {
status: false};
}if (this.onlineY(p1, p2)) {var min = p1.y > p2.y ? p2.y : p1.y;
min = min + 1;var max = p1.y > p2.y ? p1.y : p2.y;for (min; min < max; min++) {var p = {x: p1.x, y: min};if (!this.isEmpty(p)) {
console.log('有障礙物p點………………');
console.log(p);this.path = [];break;
}this.path.push(p);
}if (min == max) {return {
status: true,
data: this.path,
dir: 'y' //y軸 };
}this.path = [];return {
status: false};
}else if (this.onlineX(p1, p2)) {var j = p1.x > p2.x ? p2.x : p1.x;
j = j + 1;var max = p1.x > p2.x ? p1.x : p2.x;for (j; j < max; j++) {var p = {x: j, y: p1.y};if (!this.isEmpty(p)) {
console.log('有障礙物p點………………');
console.log(p);this.path = [];break;
}this.path.push(p);
}if (j == max) {return {
status: true,
data: this.path,
dir: 'x' //x軸 };
}this.path = [];return {
status: false};
}return {
status: false};//2點是否有其中一點被全包圍,若有,則返回trueisWrap: function (p1, p2) {//有一點為空,則條件不成立if (!this.isEmpty({x: p1.x, y: p1.y + 1}) && !this.isEmpty({
x: p1.x,
y: p1.y - 1}) && !this.isEmpty({
x: p1.x - 1,
y: p1.y
}) && !this.isEmpty({x: p1.x + 1, y: p1.y})) {return true;
}if (!this.isEmpty({x: p2.x, y: p2.y + 1}) && !this.isEmpty({
x: p2.x,
y: p2.y - 1}) && !this.isEmpty({
x: p2.x - 1,
y: p2.y
}) && !this.isEmpty({x: p2.x + 1, y: p2.y})) {return true;
}return false;
} //兩點在一條直線上,不能直線連接但是可以連通LineLink: function (p1, p2) {var pt0, pt1, pt2, pt3;//如果都在x軸,則自左至右掃描可能的路徑,//每次構造4個頂點pt0, pt1, pt2, pt3,然后看他們兩兩之間是否連通if (this.onlineX(p1, p2)) {for (var i = 0; i < this.H; i++) {if (i == p1.y) {continue;
}
pt0 = p1;
pt1 = {x: p1.x, y: i};
pt2 = {x: p2.x, y: i};
pt3 = p2;//如果頂點不為空,則該路不通。if (!this.isEmpty(pt1) || !this.isEmpty(pt2)) {continue;
}if (this.hasLine(pt0, pt1).status && this.hasLine(pt1, pt2).status && this.hasLine(pt2, pt3).status) {this.drawLine(2, [pt0, pt3, pt1, pt2]);return [pt0, pt1, pt2, pt3];
}
}
}//如果都在y軸,則自上至下掃描可能的路徑,//每次構造4個頂點pt0, pt1, pt2, pt3,然后看他們兩兩之間是否連通if (this.onlineY(p1, p2)) {for (var j = 0; j < this.W; j++) {if (j == p1.x) {continue;
}
pt0 = p1;
pt1 = {x: j, y: p1.y};
pt2 = {x: j, y: p2.y};
pt3 = p2;//如果頂點不為空,則該路不通。if (!this.isEmpty(pt1) || !this.isEmpty(pt2)) {continue;
}if (this.hasLine(pt0, pt1).status && this.hasLine(pt1, pt2).status && this.hasLine(pt2, pt3).status) {this.drawLine(2, [pt0, pt3, pt1, pt2]);return [pt0, pt1, pt2, pt3];
}
}
}
}, //兩點不在一條直線上,看是否可通curveLink: function (p1, p2) {var pt0, pt1, pt2, pt3;//特殊情況,先判斷是否是一個轉彎var spec1 = {x: p1.x, y: p2.y},
spec2 = {x: p2.x, y: p1.y};if (this.isEmpty(spec1)) {if (this.hasLine(p1, spec1).status && this.hasLine(p2, spec1).status) {
console.log('1個轉彎');this.drawLine(1, [p1, p2, spec1]);return [p1, p2, spec1];
}
}if (this.isEmpty(spec2)) {if (this.hasLine(p1, spec2).status && this.hasLine(p2, spec2).status) {
console.log('1個轉彎');// console.table([pt0, spec2, pt3]);this.drawLine(1, [p1, p2, spec2]);return [p1, spec2, p2];
}
}//先縱向掃描可能的路徑//同樣,每次構造4個頂點,看是否可通for (var k = 0; k <= this.H; k++) {
pt0 = p1;
pt1 = {x: p1.x, y: k};
pt2 = {x: p2.x, y: k};
pt3 = p2;//2個交點都為空if (this.isEmpty(pt1) && this.isEmpty(pt2)) {//2個轉彎if (this.hasLine(pt0, pt1).status && this.hasLine(pt1, pt2).status && this.hasLine(pt2, pt3).status) {
console.log('2個轉彎');this.drawLine(2, [pt0, pt3, pt1, pt2]);return [pt0, pt3, pt1, pt2];
}
}
}//橫向掃描所有可能的路徑for (var k = 0; k <= this.W; k++) {
pt0 = p1;
pt1 = {x: k, y: p1.y};
pt2 = {x: k, y: p2.y};
pt3 = p2;//2個交點都為空if (this.isEmpty(pt1) && this.isEmpty(pt2)) {//2個轉彎if (this.hasLine(pt0, pt1).status && this.hasLine(pt1, pt2).status && this.hasLine(pt2, pt3).status) {
console.log('2個轉彎');this.drawLine(2, [pt0, pt3, pt1, pt2]);return [pt0, pt3, pt1, pt2];
}
}
}return false;
}以上是web開發中連連看小游戲的制作案例的所有內容,感謝各位的閱讀!相信大家都有了一定的了解,希望分享的內容對大家有所幫助,如果還想學習更多知識,歡迎關注億速云行業資訊頻道!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。