Splines(樣條曲線)

周一到周五，每天一篇，北京時間早上7點準時更新~

A spline is effectively a long curve made up of several smaller curves (such as Béziers) that locally define their shape. At least the control points representing the ends of the curves are shared between segments, and often one or more of the interior control points are either shared or linked in some way between adjacent segments. Any number of curves can be joined together in this way, allowing arbitrarily long paths to be formed. Take a look at the curve shown in Figure 4.16

一個spline是由很多條小的曲線組成(比如貝塞爾曲線)，這些小段曲線組合起來定義了他們的形狀。其中各個小段的端點是各個小段共享的。 這樣的小段連起來，就可以長成任意模樣，我們可以來看看圖4.16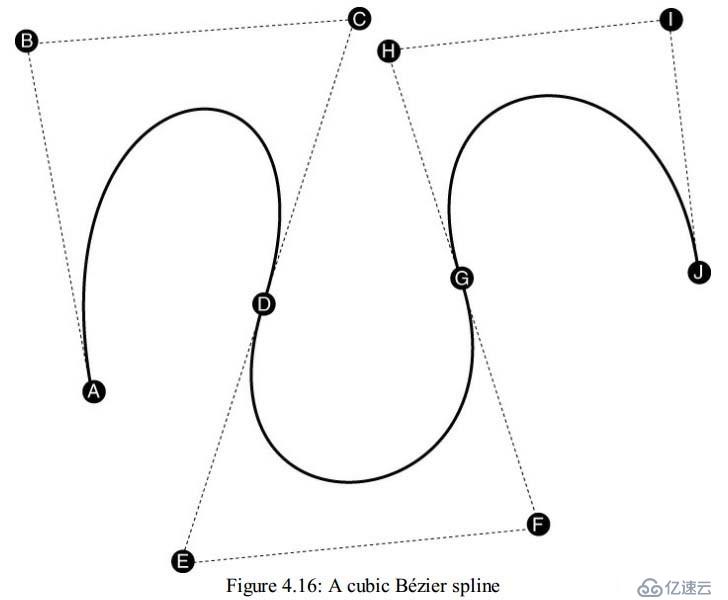

In Figure 4.16, the curve is defined by ten control points, A through J, which form three cubic Bézier curves. The first is defined by A, B, C, and D, the second shares D and further uses E, F, and G, and the third shares G and adds H, I, and J. This type of spline is known as a cubic Bézier spline because it is constructed from a sequence of cubic Bézier curves. This is also known as a cubic B-spline—a term that may be familiar to anyone who has read much about graphics in the past. To interpolate point P along the spline, we simply divide it into three regions, allowing t to range from 0.0 to 3.0. Between 0.0 and 1.0, we interpolate along the first curve, moving from A to D. Between 1.0 and 2.0, we interpolate along the second curve, moving from D to G. When t is between 2.0 and 3.0, we interpolate along the final curve between G and J. Thus, the integer part of t determines the curve segment along which we are interpolating and the fractional part of t is used to interpolate along that segment. Of course, we can scale t as we wish. For example, if we take a value between 0.0 and 1.0 and multiply it by the number of segments in the curve, we can continue to use our original range of values for t regardless of the number of control points in a curve. The following code will interpolate a vector along a cubic Bézier spline with ten control points (and thus three segments):

上圖中的曲線由10個控制點定義，A到J，他們構成了三個三次方的貝塞爾曲線。這種樣條曲線就叫做三次方貝塞爾樣條曲線，因為他們是由一系列的三次方貝塞爾曲線構成。簡稱cubic B-Spline。 為了在這條曲線上進行插值，我們可以讓t從0到3變化，0到1的時候，在第一條貝塞爾曲線上插值，1~2的時候再第二條貝塞爾曲線上插值，2~3的時候在第三條貝塞爾曲線上插值。每個小分段上，都可以看成 是在0~1上進行插值，下面展示了插值的代碼：

vec4 cubic_bspline_10(vec4 CP[10], float t)
{
float f = t 3.0;
int i = int(floor(f));
float s = fract(t);
if (t <= 0.0)
return CP[0];
if (t >= 1.0)
return CP[9];
vec4 A = CP[i 3];
vec4 B = CP[i 3 + 1];
vec4 C = CP[i 3 + 2];
vec4 D = CP[i * 3 + 3];
return cubic_bezier(A, B, C, D, s);
}
If we use a spline to determine the position or orientation of an object, we will find that we must be very careful about our choice of control point locations to keep motion smooth and fluid. The rate of change in the value of our interpolated point P (i.e., its velocity) is the differential of the equation of the curve with respect to t. If this function is discontinuous, then P will suddenly change direction and our objects will appear to jump around. Furthermore, the rate of change of P ’s velocity (its acceleration) is the second-order derivative of the spline equation with respect to t. If the acceleration is not smooth, then P will appear to suddenly speed up or slow down.

當我們使用spline去驅動物體的位置和朝向的時候，我們必須非常小心的選擇控制點的位置來讓這些運動變得平滑，這里在p點的變化率是曲線對t求偏導數。 如果這個函數不是連續的，那么我們的物體的運動則會不連續。另一方面在p點加速度是spline對t求二階偏導數，如果加速度的變化不是連續的，那么你的物體則會一會快一會慢。 讓你蛋疼菊緊，懷疑人生，從此不再相信愛情。對于這種同學，我們推薦你去攪基，但我們是不攪基滴！筆直的男子漢，無法掰彎。

A function that has a continuous first derivative is known as C1 continuous; similarly, a curve that has a continuous second derivative is known as C2 continuous. Bézier curve segments are both C1 and C2 continuous, but to ensure that we maintain continuity over the welds of a spline, we need to ensure that each segment starts off where the previous ended in terms of position, direction of movement, and rate of change. A rate of travel in a particular direction is simply a velocity. Thus, rather than assigning arbitrary control points to our spline, we can assign a velocity at each weld. If the same velocity of the curve at each weld is used in the computation of the curve segments on either side of that weld, then we will have a spline function that is both C1 and C2 continuous. This should make sense if you take another look at Figure 4.16—there are no kinks and the curve is nice and smooth through the welds (points D and G). Now look at the control points on either side of the welds. For example, take points C and E, which surround D. C and E form a straight line and D lies right in the middle of it. In fact, we can call the line segment from D to E the velocity at D, or . Given the position of point D (the weld) and the velocity of the curve at D, then C and E can be calculated as

一個函數有一節連續偏導數，我們叫它C1連續，類似的，一個曲線由二階連續偏導數，我們管它叫C2連續。貝塞爾曲線同時擁有C1和C2，為了保證spline曲線的連接處也是連續的， 我們需要讓后面的貝塞爾曲線的起始位置的狀態繼承前一段貝塞爾曲線的終點的狀態(位置和朝向以及那些變化率)，這樣他們連起來就是連續的。如果在兩個連接點兩邊的變化的速率都一樣， 那么我們認為這樣的spline就是C1和C2兩個屬性都具備的。同志們不妨再看一眼圖4.16，連接處是多么的光滑，一點也不擰巴。 現在我們看看兩邊的控制點比如C和E，他們就是在D點兩邊的，C和E在穿過D點的直線上。實際上，我們稱D到E為D點的速度，有了D點的位置和D點的速度速度，C和E就可以被求出來了

Likewise, if represents the velocity at A, B can be calculated as(同樣，A和B可以被這么求出來)

Thus, you should be able to see that given the positions and velocities at the welds of a cubic B-spline, we can dispense with all of the other control points and compute them on the fly as we evaluate each of the control points. A cubic B-spline represented this way (as a set of weld positions and velocities) is known as a cubic Hermite spline, or sometimes simply a cspline. The cspline is an extremely useful tool for producing smooth and natural animations

這樣一來，你就可以通過B-spline上給定某個連接點處的位置和速度去實時的求得這些控制點，并進而進行相關插值。這樣表達B-Spline的方式被叫做cubic hermite spline,或者簡稱cspline.cspline在 制作平滑自然的動畫的時候是非常有用的工具。

本日的翻譯就到這里，明天見，拜拜~~

第一時間獲取最新橋段，請關注東漢書院以及圖形之心公眾號

東漢書院，等你來玩哦