Projection Transformations(投影變換)

周一到周五，每天一篇，北京時間早上7點準時更新~

The projection transformation is applied to your vertices after the model–view transformation. This projection actually defines the viewing volume and establishes clipping planes(投影變換發生在模型視口變換之后，這個矩陣定義了視錐體和剪裁平面們). The clipping planes are plane equations in 3D space that OpenGL uses to determine whether geometry can be seen by the viewer(剪裁平面定義在3D空間中，OpenGL使用這些剪裁平面去判斷哪些幾何物體是可以被看見的). More specifically, the projection transformation specifies how a finished scene (after all the modeling is done) is projected to the final image on the screen(更確切的說，投影變換決定了3D場景如何投影成為一張2D畫面). You learn more about two types of projections—orthographic and perspective(你將會學到更多關于兩種投影矩陣的東西-正交投影和透視投影). In an orthographic, or parallel, projection, all the polygons are drawn on screen with exactly the relative dimensions specified(在正交投影中、所有的多邊形保持不變). Lines and polygons are mapped directly to the 2D screen using parallel lines, which means no matter how far away something is, it is still drawn the same size, just flattened against the screen(也就是說，無論物體離觀察者多遠，物體的大小都保持不變). This type of projection is typically used for rendering two-dimensional images such as the front, top, and side elevations in blueprints or two-dimensional graphics such as text or on-screen menus(這種模式尤其適合去做2D畫面). A perspective projection shows scenes more as they appear in real life instead of as a blueprint(透視投影會產生近大遠小的效果，就如同你生活中看場景的那樣). The hallmark of perspective projections is foreshortening, which makes distant objects appear smaller than nearby objects of the same size. Lines in 3D space that might be parallel do not always appear parallel to the viewer(在透視投影下，在3D世界中的線原本是平行的，但是會看起來不平行). With a railroad track, for instance, the rails are parallel, but using perspective projection, they appear to converge at some distant point(這里就舉了個例子說啥啥啥的本來是平行的，但在透視投影下不平行). The benefit of perspective projection is that you don’t have to figure out where lines converge or how much smaller distant objects are(透視投影的好處就是你不需要理會那些玩意到底有多大). All you need to do is specify the scene using the model–view transformations and then apply the perspective projection matrix(你所需要做的就是，先試用模型視口矩陣給物體變換一下，然后用透視矩陣去處理，線性代數會幫你處理好所有的問題). Linear algebra works all the magic for you. Figure 4.12 compares orthographic and perspective projections on two different scenes(圖4.12展示了正交和透視投影下的兩個不同場景的效果). As you can see in the orthographic projection shown on the left, the cubes do not appear to change in size as they move farther from the viewer(如你所見，左邊是正交投影，當立方體越來越遠的時候，大小不變). However, in the perspective projection shown on the right, the cubes get smaller and smaller as they get farther from the viewer(然而在透視投影下，距離越遠，看起來越小)

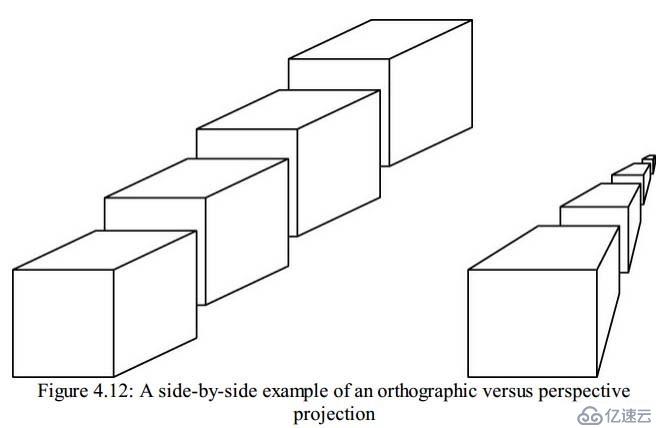
Orthographic projections are used most often for 2D drawing purposes where you want an exact correspondence between pixels and drawing units. You might use them for a schematic layout, text, or perhaps a 2D graphing application. You also can use an orthographic projection for 3D renderings when the depth of the rendering has a very small depth in comparison to the distance from the viewpoint(通常來說，正交投影適合做2D的應用，有時候也會拿去做一些深度變化不是很明顯的3D場景渲染). Perspective projections are used for rendering scenes that contain wide-open spaces or objects that need to have foreshortening applied. For the most part, perspective projections are typical for 3D graphics. In fact, looking at a 3D object with an orthographic projection can be somewhat unsettling.(透視投影則是用來做3D產品的，這種產品明顯的特點就是，需要有近大遠小的效果，實際上如果你用正交投影去顯示3D場景，你會覺得很蛋疼)

Perspective Matrices(透視矩陣)

Once your vertices are in view space, we need to get them into clip space, which we do by applying our projection matrix, which may represent a perspective or orthographic projection (or some other projection)(當你當你的頂點數據在視口空間下了之后，你需要把他們玩到剪裁坐標系里去，在這里進行投影變換). A commonly used perspective matrix is a frustum matrix. A frustum matrix is a projection matrix that produces a perspective projection such that clip space takes the shape of a rectangular frustum, which is a truncated rectangular pyramid. Its parameters are the distance to the near and far planes and the world-space coordinate of the left, right, top, and bottom clipping planes. A frustrum matrix takes the following form:(一個常見的透視矩陣就是視錐體矩陣，視錐體矩陣是一個透視矩陣，你需要指定左右上下近剪裁面遠剪裁面來定義這個矩陣，它呈現的形狀則是倒金字塔形，下面展示了產生視錐體的函數)

static inline mat4 frustum(float left,
float right,
float bottom,
float top,
float n,
float f) { ... }
Another common method for constructing a perspective matrix is to directly specify a field of view as an angle (in degrees, perhaps), an aspect ratio (generally derived by dividing the window’s width by its height), and the view-space positions of the near and far planes. This is somewhat simpler to specify, and produces only symmetric frustra. However, this is almost always what you’ll want. The vmath function to do this is vmath::perspective:(另一種指定投影矩陣的方式就是直接指定視口的可見角度、長寬比、近剪裁面遠剪裁面。我們的教學體系中使用的就是第二種方式，同時數學課中也推導了這些矩陣的來歷。vmath的相關接口如下)

static inline mat4 perspective(float fovy / in degrees /,
float aspect,
float n,
float f) { ... }
Orthographic Matrices(正交矩陣)

If you wish to use an orthographic projection for your scene, then you can construct a (somewhat simpler) orthographic projection matrix(如果你想對你的場景使用正交變換，那么你可以構建一個正交投影矩陣). An orthographic projection matrix is simply a scaling matrix that linearly maps view-space coordinates into clip-space coordinates(一個正交投影矩陣就是線性的將視口空間下的玩意映射到剪裁空間里去). The parameters to construct the orthographic projection matrix are the left, right, top, and bottom coordinates in view space of the bounds of the scene, and the position of the near and far planes. The form of the matrix is(構建這樣的矩陣的參數是：左右上下、近剪裁面，遠剪裁面，矩陣的形式如下圖所示)

Again, there’s a vmath function to construct this matrix for you, vmath::ortho:(vmath庫中創建正交矩陣的接口如下：)

static inline mat4 ortho(float left,
float right,
float bottom,
float top,
float near,
float far) { ... }
本日的翻譯就到這里，明天見，拜拜~~

第一時間獲取最新橋段，請關注東漢書院以及圖形之心公眾號

東漢書院，等你來玩哦