您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
只怪 博主智商無下限,花了一個周末終于把系數矩陣的壓縮存儲及其轉置給弄明白了,所以今天就和大家分享一下我的學習過程啦!!!
稀疏矩陣是指矩陣中大多數元素為零的矩陣,從直觀上講,非零元素的個數低于總元素的30%時,這樣的矩陣稱為稀疏矩陣。

1.稀疏矩陣的三元組組表示法
對于稀疏矩陣的壓縮存儲,采取只存儲非零元素的方法,由于稀疏矩陣中非零元素的分布沒有規律,所以呢???在存儲非零元素的時候必須給每個元素做個標記(非零元素在矩陣中所處的行號和列號)。
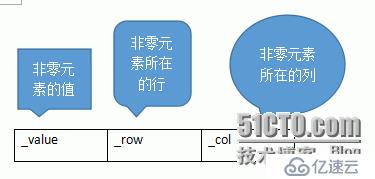
//稀疏矩陣三元組表類型的定義
struct Triple
{
T _value;
size_t _row;
size_t _col;
Triple(size_t row=0,size_t col=0,const T& value=T())
:_value(value)
,_row(row)
,_col(col)
{}
};(1)Triple是包含三個域的結構體類型,其元素是為了存儲非零元的三元組
2.稀疏矩陣的壓縮存儲
就上圖給出的矩陣而言,運用三元組壓縮存儲的方法存儲后的結果是醬紫滴

源代碼是醬紫滴:
//用三元組表示實現稀疏矩陣的壓縮存儲
SpareMatrix(T* a,size_t m,size_t n,const T& invalid)
:_rowsize(m)
,_colsize(n)
,_invalid(invalid)
{
for(size_t i=0;i<m;i++)
{
for(size_t j=0;j<n;j++)
{
if(a[i*n+j]!=invalid)
{
_a.push_back(Triple<T>(i,j,a[i*n+j]));
}
}
}
}3.稀疏矩陣的列序遞增轉置法
采用被轉置矩陣按照列序遞增的的順序進行轉置,并依此將將其送入轉置后的三元組表中,這樣子的話轉置后的三元組表恰好是以行序號為主的哦 。
具體做法:
(1)找出轉置后的第一行元素:第一遍從頭至尾掃描三元組表,找出所有_col為1的三元組,轉置后按順序放到開辟好新的三元組表中
(2)找出轉置后的第二行元素:第一遍從頭至尾掃描三元組表,找出所有_col為2的三元組,轉置后按順序放到開辟好新的三元組表中
源代碼是醬紫滴:
//稀疏矩陣的轉置
SpareMatrix<T> Transport()
{
SpareMatrix<T> tmp;
tmp._rowsize = _colsize;
tmp._colsize = _rowsize;
tmp._invalid=_invalid;
//給構建好的匿名對象開辟空間,但是不改變size的大小,開辟后初始化的值為原來的。
tmp._a.reserve(_a.size());
for(size_t i=0;i<_colsize;i++)
{
size_t index=0;
for(index=0;index<_a.size();index++)
{
if(_a[index]._col==i)
{
Triple <T> tp;
tp._row=_a[index]._col;
tp._col=_a[index]._row;
tp._value=_a[index]._value;
tmp._a.push_back(tp);
}
}
}
return tmp;
}注釋:雖然構建了一個 SpareMatrix<T> tmp類型的對象但是并沒有給它開辟和_a一樣大小的空間,所以要調用reserve或者resize兩個函數中任意一個即可,否則當你在運行程序的時候會奔潰哦,智商無下線的博主昨天就是犯了這個錯誤,程序跑起來的時候,老是彈出這樣的框框:
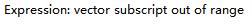
最后調試了好久才發現問題所在 氣死寶寶啦,
氣死寶寶啦,
算法分析:
算法主要耗費在雙重循環中,其時間復雜度為o(_colsize*_a.size());
4.稀疏矩陣的一次定位快速轉置算法
算法思想:
(1)計算待轉置矩陣三元組表中每一列非零元素的個數,即轉置后矩陣三元組表每一行中非零元素的個數。
(2)計算待轉置矩陣每一列中第一個非零元素三元組表中的具體位置。
源代碼是醬紫滴:
/稀疏矩陣的快速轉置
SpareMatrix<T> FastTransport()
{
SpareMatrix<T> tmp;
tmp._rowsize = _colsize;
tmp._colsize = _rowsize;
tmp._invalid=_invalid;
int* rowcounts=new int[tmp._rowsize];
int* rowstart=new int[tmp._rowsize];
memset(rowcounts,0,sizeof((int*)_colsize));
memset(rowstart,0,sizeof((int*)_colsize));
size_t index=0;
//計算待轉置矩陣每一列非零元素的個數
while(index<_a.size())
{
rowcounts[_a[index]._col]++;
index++;
}
//計算待轉置矩陣每一列第一個非零元素在三元組表中的位置
rowstart[0]=0;
for(size_t i=1;i<_colsize;i++)
{
rowstart[i]=rowstart[i-1]+rowcounts[i-1];
}
index=0;
//給_a的匿名對象開辟_a大小的空間
tmp._a.resize(_a.size());
while(index<_a.size())
{/*
size_t rowindex=_a[index]._col;*/
int& start=rowstart[_a[index]._col];
Triple<T> tp;
tp._value=_a[index]._value;
tp._row=_a[index]._col;
tp._col=_a[index]._row;
tmp._a[start++]=tp;
index++;
}
return tmp;
}算法分析:
一次定位快速轉置算法時間主要耗費在三個并列的循環中,因而時間復雜度為o(_a.size+_colsize).
完整的源代碼:
//稀疏矩陣的壓縮存儲
#include<iostream>
#include<vector>
using namespace std;
template<typename T>
//稀疏矩陣三元組表類型的定義
struct Triple
{
T _value;
size_t _row;
size_t _col;
Triple(size_t row=0,size_t col=0,const T& value=T())
:_value(value)
,_row(row)
,_col(col)
{}
};
template<typename T>
//稀疏矩陣
class SpareMatrix
{
public:
SpareMatrix()
:_rowsize(0)
,_colsize(0)
,_invalid(0)
{}
//用三元組表示實現稀疏矩陣的壓縮存儲
SpareMatrix(T* a,size_t m,size_t n,const T& invalid)
:_rowsize(m)
,_colsize(n)
,_invalid(invalid)
{
for(size_t i=0;i<m;i++)
{
for(size_t j=0;j<n;j++)
{
if(a[i*n+j]!=invalid)
{
_a.push_back(Triple<T>(i,j,a[i*n+j]));
}
}
}
}
//稀疏矩陣的轉置
SpareMatrix<T> Transport()
{
SpareMatrix<T> tmp;
tmp._rowsize = _colsize;
tmp._colsize = _rowsize;
tmp._invalid=_invalid;
//給構建好的匿名對象開辟空間,但是不改變size的大小,開辟后初始化的值為原來的。
tmp._a.reserve(_a.size());
for(size_t i=0;i<_colsize;i++)
{
size_t index=0;
for(index=0;index<_a.size();index++)
{
if(_a[index]._col==i)
{
Triple <T> tp;
tp._row=_a[index]._col;
tp._col=_a[index]._row;
tp._value=_a[index]._value;
tmp._a.push_back(tp);
}
}
}
return tmp;
}
//稀疏矩陣的快速轉置
SpareMatrix<T> FastTransport()
{
SpareMatrix<T> tmp;
tmp._rowsize = _colsize;
tmp._colsize = _rowsize;
tmp._invalid=_invalid;
int* rowcounts=new int[tmp._rowsize];
int* rowstart=new int[tmp._rowsize];
memset(rowcounts,0,sizeof((int*)_colsize));
memset(rowstart,0,sizeof((int*)_colsize));
size_t index=0;
//計算待轉置矩陣每一列非零元素的個數
while(index<_a.size())
{
rowcounts[_a[index]._col]++;
index++;
}
//計算待轉置矩陣每一列第一個非零元素在三元組表中的位置
rowstart[0]=0;
for(size_t i=1;i<_colsize;i++)
{
rowstart[i]=rowstart[i-1]+rowcounts[i-1];
}
index=0;
//給_a的匿名對象開辟_a大小的空間
tmp._a.resize(_a.size());
while(index<=_a.size())
{/*
size_t rowindex=_a[index]._col;*/
int& start=rowstart[_a[index]._col];
Triple<T> tp;
tp._value=_a[index]._value;
tp._row=_a[index]._col;
tp._col=_a[index]._row;
tmp._a[start++]=tp;
index++;
}
return tmp;
}
void display()
{
size_t index=0;
for(size_t i=0;i<_rowsize;i++)
{
for(size_t j=0;j<_colsize;j++)
{
if(index<_a.size() && _a[index]._row==i && _a[index]._col==j)
{
cout<<_a[index++]._value<<" ";
}
else
{
cout<<_invalid<<" ";
}
}
cout<<endl;
}
cout<<endl;
}
protected:
vector<Triple <T> > _a;
size_t _rowsize;
size_t _colsize;
T _invalid;
};
void test()
{
int a[4][4]={{1,0,0,0},
{2,2,0,0},
{0,1,3,0},
{1,0,0,4}};
SpareMatrix<int>sm1((int*)a,4,4,0);
sm1.display();
SpareMatrix<int> sm2=sm1.Transport();
sm1.display();
SpareMatrix<int> sm3=sm1.FastTransport();
sm1.display();
}
int main()
{
test();
getchar();
return 0;
}免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。