您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
什么是時間復雜度與空間復雜度?相信很多人對時間復雜度與空間復雜度的了解處于懵懂狀態,小編給大家總結了以下內容。如下資料是關于復雜度與空間復雜度的內容。
1、時間復雜度
所謂時間復雜度實際上就是函數,既是函數計算執行的基本操作次數。ps:這里的函數是指數學里面的函數,而不是C語法里的函數。
如下面這個代碼:
void Test1 ( int N )
{
for (int i = 0; i < N ; ++ i)
{
for (int j = 0; j < N ; ++ j)
{
//...
}
}
for (int k = 0; k < 2 * N ; ++ k)
{
//...
}
int count = 10;
while (count --)
{
//...
}
}
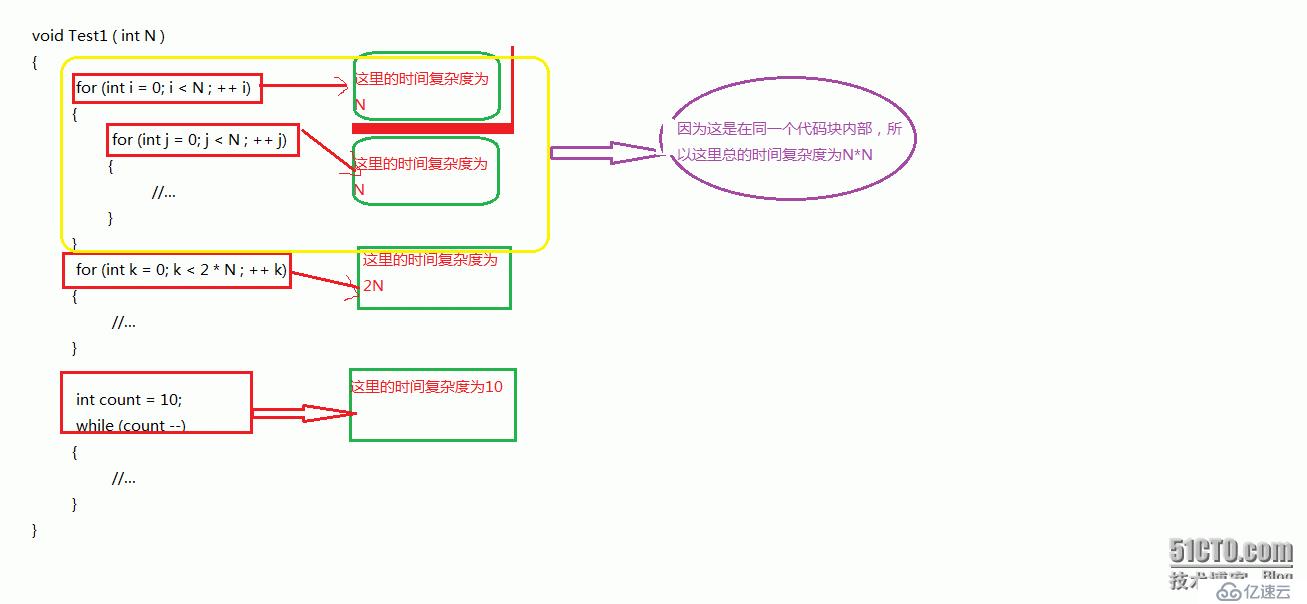
所以這段代碼的時間復雜度是: F(N) = N^2 + 2N + 10,這個時間計算的就是時間復雜度。
算法分析的分類
最壞情況:任意輸入規模的最大運行時間。(上界)
平均情況:任意輸入規模的期望運行時間。
最好情況:任意輸入規模的最小運行時間,通常最好情況不會出現。(下界)
例如:在一個長度為N的線性表中搜索一個數據x。
最壞情況:N次比較。
平均情況:N/2次比較。
最好情況:1次比較。
在實際中我們通常情況考量的是算法的最壞運行情況。也就是說對于任意輸入規模N,算法的最長運行時間,理由如下:
一個算法的最壞情況的運行時間是在任意輸入下的運行時間上界。
對于某些算法,最壞的情況出現的較為頻繁。
大體上看,平均情況與最壞情況一樣差。
算法分析要保持大局觀:
忽略掉那些的常數。
關注運行時間的增長趨勢,關注函數式中增長最快的表達式。
O的漸進表示法(Big O Notation)
通常我們使用O記號法表示最壞運行情況的漸進上界。其實也就是說我們使用O標記法表示時間復雜度,一般關注的是算法運行的最壞情況。
下面我們使用大O的漸進表示法計算下面函數的時間復雜度
如:F(N) = N^3 + N^2 + N +1000,則關注N^3->O(N^3)
【1.一般算法的時間復雜度計算】
void Test1 ( int N )
{
for (int i = 0; i < N ; ++ i)
{
for (int j = 0; j < N ; ++ j)
{
//...
}
}
for (int k = 0; k < 2 * N ; ++ k)
{
//...
}
int count = 10;
while (count --)
{
//...
}
}
Test1的時間復雜度為:O(N^2)
void Test2 (int N, int M)
{
for (int i = 0; i < M ; ++i)
{
}
for (int k = 0; k < N ; ++k)
{
//...
}
}
Test2的時間復雜度為:O(M+N)
void Test3 (int N, int M)
{
for (int i = 0; i < M ; ++i)
{
for (int j = 0; j < N ; ++j)
{
//...
}
}
}
Test3的時間復雜度為:O(M*N)
【2.遞歸算法的時間復雜度計算】
遞歸算法的時間復雜度為遞歸總次數*每次遞歸次數。
空間復雜度
空間復雜度的計算跟時間復雜度類似,也使用大O的漸進表示法。--(對象的個數)
要注意的是遞歸算法的空間復雜度,假如遞歸深度為N*每次遞歸的空間大小為1,則空間復雜度為O(N)。
以斐波那契數列為例:
#include<iostream>
#include<stdlib.h>
using namespace std;
//斐波那契數列的遞歸算法(一般解法)
int Fib(int N )
{
return N < 2 ? N : Fib( N - 1) + Fib( N - 2);
}
int main()
{
int ret=Fib(0);
cout << ret << endl;
system( "pause");
return 0;
}


此代碼的空間復雜度是:O(N),既是深度。
時間復雜度是:O(2^N).
這段代碼有下面幾個明顯缺陷:
1、遞歸時會有函數的壓棧開銷。
2、有重復計算。
所以我們需要對這段代碼進行優化。請看下面:
方法一:可以倒著計算,定義三個變量,如下所示:
long long Fib(size_t N )
{
long long * Fibarray = new long long[ N + 1];
Fibarray[0] = 0;
Fibarray[1] = 1;
for ( int i = 2; i <= N; ++i)
{
Fibarray[i] = Fibarray[i - 1] + Fibarray[i - 2];
}
long long ret = Fibarray[ N];
delete[] Fibarray;
return ret;
}
此方法的時間復雜度為:O(N)。
空間復雜度為:O(N)。
方法二:用一個循環開辟一個數組。
long long Fib(size_t N )
{
long long Fib[3] = { 0, 1, N };
for ( int i = 2; i <= N; ++i)
{
Fib[2] = Fib[1] + Fib[0];
Fib[0] = Fib[1];
Fib[1] = Fib[2];
}
return Fib[2];
}
這種方法的時間復雜度是:O(N)。
空間復雜度是:O(1),因為常數個對象。
看完上訴內容,你們對時間復雜度與空間復雜度大概了解了嗎?如果想了解更多相關文章內容,歡迎關注億速云行業資訊頻道,感謝各位的閱讀!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。