如何解析Java 數據結構中時間復雜度與空間復雜度

這篇文章給大家介紹如何解析Java 數據結構中時間復雜度與空間復雜度，內容非常詳細，感興趣的小伙伴們可以參考借鑒，希望對大家能有所幫助。

算法效率

在使用當中，算法效率分為兩種，一是時間效率(時間復雜度)，二是空間效率(空間復雜度)。時間復雜度是指程序運行的速度。空間復雜度是指一個算法所需要的額外的空間。

時間復雜度

什么是時間復雜度

計算程序運行的時間不能拿簡單的時間來計算，因為不同處理器處理數據的能力是不一樣的。所以只算一個大概的次數就行了，儼然就是算法中的基本操作的執行次數。用大O的漸進法來表示

例：計算 func1 的基本操作執行了幾次

void func1(int N){
    int count = 0;
    for (int i = 0; i < N ; i++) {
        for (int j = 0; j < N ; j++) {
            count++;
        }
    }
    for (int k = 0; k < 2 * N ; k++) {
        count++;
    }
    int M = 10;
    while ((M--) > 0) {
        count++;
    }
    System.out.println(count);
}

func1 的基本執行次數是：F(N) = N^2 + 2*N + 10

推導大 O 階的方法

1、用常數1取代運行時間中的所有加法常數。
2、在修改后的運行次數函數中，只保留最高階項。
3、如果最高階項存在且不是1，則去除與這個項目相乘的常數。得到的結果就是大O階。

所以使用大 O 的漸進法表示之后，func1 的時間復雜度就是：O(N^2)

算法情況

因為當我們用算法計算的時候，會有最好情況和最壞情況和平均情況。我們常說的時間復雜度在 O(N) 這里的時間復雜度就是最壞情況。
最好情況就是最小的運行次數。

舉例一：

void func2(int N){
    int count = 0;
    for (int k = 0; k < 2 * N ; k++) {
        count++;
    }
    int M = 10;
    while ((M--) > 0) {
        count++;
    }
    System.out.println(count);
}

這里的結果是 O(N) 因為根據時間復雜度的計算方法，去除常數，所以 2*N 就是 N 。M 是 10 也可以忽略掉。

舉例二：

void func3(int N, int M) {
    int count = 0;
    for (int k = 0; k < M; k++) {
        count++;
    }
    for (int k = 0; k < N ; k++) {
        count++;
    }
    System.out.println(count);
}

這里的時間復雜度是 O(M+N) 因為 M 和 N 的值是未知的，所以是 O(M+N)

舉例三：

void func4(int N) {
    int count = 0;
    for (int k = 0; k < 100; k++) {
        count++;
    }
    System.out.println(count);
}

這個的時間復雜度是 O(1) 因為循環里面是常數，所以根據大 O 漸進法，結果就是 O(1)

計算冒泡排序的時間復雜度

public static void bubbleSort(int[] arr){
    for (int i = 0; i < arr.length; i++) {
        for (int j = 0; j < arr.length - 1 - i; j++) {
            if(arr[j] > arr[j+1]){
                int tmp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = tmp;
            }
        }
    }
}

因為冒泡排序的特殊性，可能一次就排好了，也可能得一直排到最后，所以就有了最好情況和最壞情況。

最好情況：就是比較一次，就是 O(N)
最壞情況：一直排到最后，就是 O(N^2)

計算二分查找的時間復雜度

int binarySearch(int[] array, int value) {
    int begin = 0;
    int end = array.length - 1;
    while (begin <= end) {
        int mid = begin + ((end-begin) / 2);
        if (array[mid] < value)
            begin = mid + 1;
        else if (array[mid] > value)
            end = mid - 1;
        else
            return mid;
    }
    return -1;
}

因為二分查找是一半一半的找，所以每次查找之后都會把查找范圍減半，比如說在一個 1 - 8 的有序數組里面查找 8 也就是查找最壞情況。圖示如下：

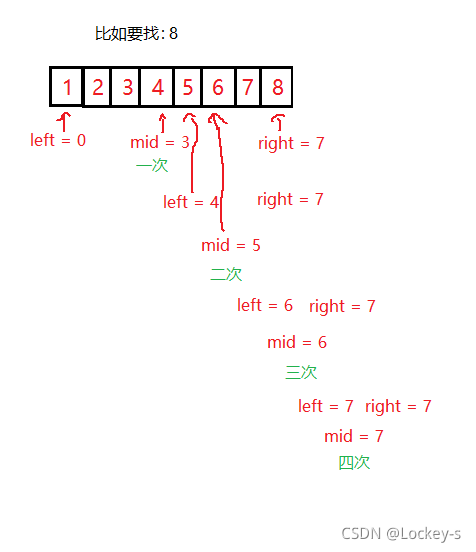
如圖，在數組當中完成二分查找需要 log2n - 1 次也就是時間復雜度是 log2n （就是 log 以 2 為底 n 的對數）

計算階乘遞歸的時間復雜度

long factorial(int N) {
	return N < 2 ? N : factorial(N-1) * N;
}

計算遞歸的時間復雜度：遞歸的次數 * 每次遞歸執行的次數。

所以這次遞歸的時候，基本操作遞歸了 N 次，所以時間復雜度就是 O(N)

計算斐波那契遞歸的時間復雜度

int fibonacci(int N) {
	return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);
}

假設 N 是 5 我們來展開求

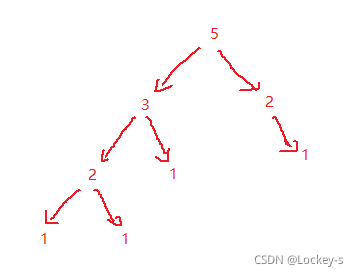
如圖：每次計算都會計算下一層，但是每次都是一邊少，一邊多。所以就可以直接按照每邊一樣來計算。如下圖：

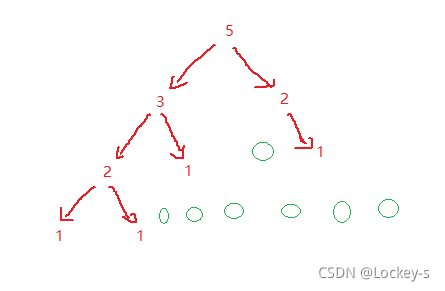
所以就有公式可以計算出每次計算的次數，就是：2 ^ (n - 1) ，所以計算的結果就是：2^\0 + 2^1 + 2^2 + 2^3……2^(n-1) = 2^n+1 所以按照大 O 漸進法來算，結果就是：2^n 。

所以斐波那契數列的時間復雜度就是：2^n 。

空間復雜度

空間復雜度衡量的是一個算法在運行過程當中占用的額外存儲空間的大小，因為沒必要按照字節來算，而是算變量的個數。也是用大 O 漸進法表示。

計算冒泡排序的空間復雜度

public static void bubbleSort(int[] arr){
    for (int i = 0; i < arr.length; i++) {
        for (int j = 0; j < arr.length - 1 - i; j++) {
            if(arr[j] > arr[j+1]){
                int tmp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = tmp;
            }
        }
    }
}

因為冒泡排序的變量并沒有變化，使用的是額外空間是常數，所以空間復雜度是 O(1) 。

計算斐波那契數列的空間復雜度（非遞歸）

int[] fibonacci(int n) {
    long[] fibArray = new long[n + 1];
    fibArray[0] = 0;
    fibArray[1] = 1;
    for (int i = 2; i <= n ; i++) {
        fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
    }
    return fibArray;
}

因為這里的斐波那契數列開辟了 n 個額外空間，所以空間復雜度為 O(n) 。

計算階乘遞歸Factorial的時間復雜度

int factorial(int N) {
	return N < 2 ? N : factorial(N-1)*N;
}

因為是遞歸，每次遞歸都會開辟棧幀，每個棧幀占用常數個空間，所以空間復雜度就是 O(N) 。

關于如何解析Java 數據結構中時間復雜度與空間復雜度就分享到這里了，希望以上內容可以對大家有一定的幫助，可以學到更多知識。如果覺得文章不錯，可以把它分享出去讓更多的人看到。