您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
稀疏矩陣:矩陣中大多數元素為0的矩陣,從直觀上講,當非零元素個數低于總元素的30%時,這樣的矩陣為稀疏矩陣。
如:
int array [6][5] = {{1, 0, 3, 0, 5},
{0, 0, 0, 0, 0},
{0, 0, 0, 0, 0},
{1, 0, 3, 0, 5},
{0, 0, 0, 0, 0},
{0, 0, 0, 0, 0}};
稀疏矩陣的壓縮存儲:使用{row,col,value}三元組存儲每一個有效數據,三元組按原矩陣中的位置,以行優先級先后順序依次存放。
矩陣的轉置:將原矩陣的行、列對換,也就是將[i][j]和[j][i]位置上的數據對換。
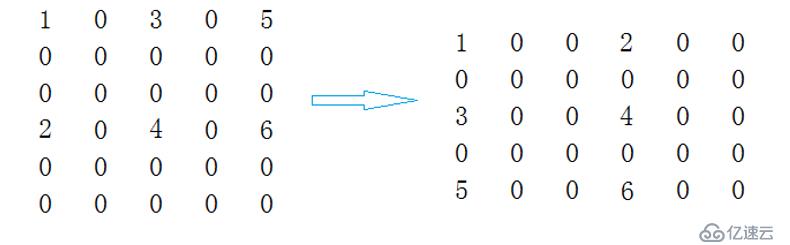
稀疏矩陣的列序遞增法:
按照被轉置矩陣三元組表A的序列(即轉置后三元組表B的行序)遞增的順序進行轉置,則轉置后矩陣的三元組表B恰好是以“行序為主序的”.
一次定位快速轉置法:
在列轉置中算法的時間浪費主要在雙重循環中,要改善算法的性能,必須去掉雙重循環,使得整個轉置過程通過一次循環來完成。
為了使得被轉置的三元組表A中元素一次定位到三元組表B中,需要計算一下以下數據:
1)RowCounts,三元組表A中每一列有效值的個數,即轉置后矩陣三元組表B中每一行有效值的個數。
2)RowStart,三元組表B中每一行有效值的起始位置。
RowStart[i] = RowStart[i - 1] + RowCounts[i - 1];
代碼實現:
#include <iostream>
using namespace std;
#include <vector>//動態數組
//三元組
template<class T>
struct Triple
{
size_t _row;
size_t _col;
T _value;
Triple(size_t row = 0, size_t col = 0, const T& value = T())
:_row(row)
, _col(col)
, _value(value)
{}
};
template<class T>
class SparseMatrix
{
public://invalid 非零值
SparseMatrix(T* a = NULL, size_t M = 0, size_t N = 0, const T& invalid = T())
:_rowSize(M)
, _colSize(N)
, _invalid(invalid)
{
for (size_t i = 0; i < M; ++i)
{
for (size_t j = 0; j < N; ++j)
{
if (a[i*N + j] != _invalid)//每行元素個數就是列的個數
{
Triple<T> t;
t._row = i;
t._col = j;
t._value = a[i*N + j];
_a.push_back(t);//在Vector類,插入一個元素
}
}
}
}
void Display()
{
size_t index = 0;
for (size_t i = 0; i < _rowSize; ++i)
{
for (size_t j = 0; j < _colSize; ++j)
{
if (index < _a.size()&& (_a[index]._row == i)&& (_a[index]._col == j))
{
cout << _a[index++]._value << " ";
}
else
{
cout << _invalid << " ";
}
}
cout << endl;
}
}
//矩陣列序遞增轉置算法,時間復雜度為O(有效數據的個數*原矩陣的列數)
SparseMatrix<T> Transport()
{
SparseMatrix<T> sm;
sm._colSize = _rowSize;
sm._rowSize = _colSize;
sm._invalid = _invalid;
for (size_t i = 0; i < _colSize; ++i)//列序遞增
{
size_t index = 0;
while (index < _a.size())
{
if (_a[index]._col == i)
{
Triple<T> t;
t._row = _a[index]._col;
t._col = _a[index]._row;
t._value = _a[index]._value;
sm._a.push_back(t);
}
++index;
}
}
return sm;
}
//一次定位計數快速轉置 時間復雜度為O(有效數據的個數+原矩陣的列數)
SparseMatrix<T> FastTransport()
{
SparseMatrix<T> sm;
sm._rowSize = _colSize;
sm._colSize = _rowSize;
sm._invalid = _invalid;
int* RowCounts = new int[_colSize];//計數
int* RowStart = new int[_colSize];//位置
memset(RowCounts, 0, sizeof(int)*_colSize);
memset(RowStart, 0, sizeof(int)*_colSize);
size_t index = 0;//index 非零元素
while (index < _a.size())
{
++RowCounts[_a[index]._col];
++index;
}
for (size_t i = 1; i < _colSize; ++i)
{
RowStart[i] = RowStart[i - 1] + RowCounts[i - 1];
}
index = 0;
sm._a.resize(_a.size());
while (index < sm._a.size())
{
Triple<T> t;
t._row = _a[index]._col;
t._col = _a[index]._row;
t._value = _a[index]._value;
sm._a[RowStart[_a[index]._col]] = t;
++RowStart[_a[index]._col];
++index;
}
delete[] RowCounts;
delete[] RowStart;
return sm;
}
protected:
vector<Triple<T>> _a;
size_t _rowSize;
size_t _colSize;
T _invalid;
};
void Test()
{
int array[5][4] =
{
{ 1, 0, 3, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 2, 0, 4, 5 },
{ 0, 0, 0, 0 },
};
SparseMatrix<int> sm1((int*)array, 5, 4, 0);
cout << "打印原矩陣:"<<endl;
sm1.Display();
cout << endl;
cout << "打印轉置后的矩陣:" << endl;
SparseMatrix<int> sm2 = sm1.Transport();
/*SparseMatrix<int> sm2 = sm1.FastTransport();*/
sm2.Display();
}
int main()
{
Test();
system("pause");
return 0;
}
運行結果:
打印原矩陣:
1 0 3 0
0 0 0 0
0 0 0 0
2 0 4 5
0 0 0 0
打印轉置后的矩陣:
1 0 0 2 0
0 0 0 0 0
3 0 0 4 0
0 0 0 5 0
請按任意鍵繼續. . .
兩種算法比較:
假設有效數據的個數為100,原矩陣的列數為100,矩陣列序遞增轉置算法,時間耗費為O(有效數據的個數*原矩陣的列數),即100*100=10000次;一次定位計數快速轉置算法,時間復雜度為O(有效數據的個數+原矩陣的列數),即100+100=200次左右。顯然一次定位計數快速轉置算法的時間效率要高的多,在時間性能上優于列序遞增轉置法,但是在空間耗費上增加了兩個輔助向量空間,即RowCounts和RowStart,由此可見,算法在時間上的節省是以更多的存儲空間為代價的。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。