常見排序算法之交換排序

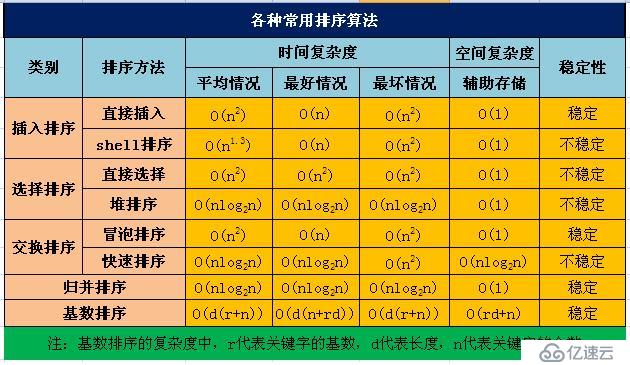
常見的交換排序算法有冒泡排序和快速排序

冒泡排序

冒泡排序算法的基本原理如下：（從后往前）

1. 比較相鄰的元素。如果第一個比第二個大，就交換他們兩個。

2. 對每一對相鄰元素作同樣的工作，從開始第一對到結尾的最后一對。在這一點，最后

3. 的元素應該會是最大的數。

4. 針對所有的元素重復以上的步驟，除了最后一個。

5. 持續每次對越來越少的元素重復上面的步驟，直到沒有任何一對數字需要比較。

經過優化過后的代碼如下：

void BubbleSort(int* a, size_t n)  //冒泡排序優化版
{
	assert(a);
	bool flag = true;
	for (int i = 0; i < n - 1 && flag; ++i)
	{
		flag = false;
		for (int j = 1; j < n - i; ++j)
		{
			if (a[j - 1] > a[j])
			{
				std::swap(a[j - 1], a[j]);
				flag = true;
			}
		}
	}
}

性能分析

若文件的初始狀態是正序的，一趟掃描即可完成排序，所以，冒泡排序最好時間

復雜度為O(N)。

若初始文件是反序的，需要進行 N -1 趟排序。每趟排序要進行 N - i 次關鍵字的

比較(1 ≤ i ≤ N - 1)。在這種情況下，比較和移動次數均達到最大值，所以，冒泡排

序的最壞時間復雜度為O(N²)。

因此，冒泡排序的平均時間復雜度為O(N²)。

總結起來，其實就是一句話：當數據越接近正序時，冒泡排序性能越好。

穩定性

冒泡排序就是把小的元素往前調或者把大的元素往后調。比較是相鄰的兩個元素比

較，交換也發生在這兩個元素之間。

所以相同元素的前后順序并沒有改變，所以冒泡排序是一種穩定排序算法。

快速排序

快速排序的基本原理：

        1.通過一趟排序將要排序的數據分割成獨立的兩部分：分割點左邊都是比它小

的數，右邊都是比它大的數。

       2. 然后再按此方法對這兩部分數據分別進行快速排序，整個排序過程可以遞歸

進行，以此達到整個數據變成有序序列。

算法示意圖如下：

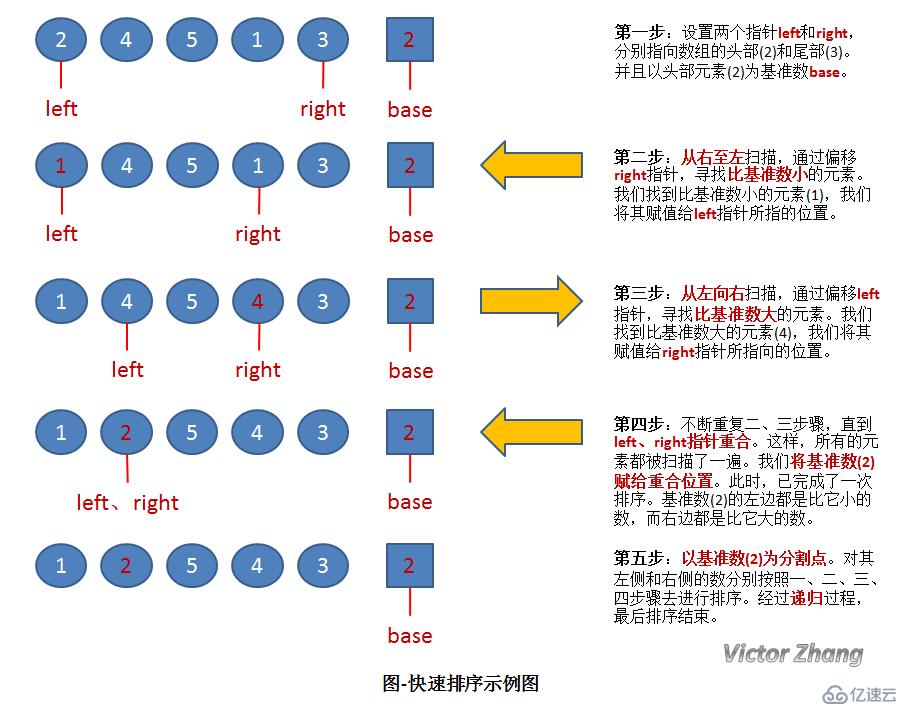
代碼如下：

比較直觀的代碼：

int Partition(int* a, int left, int right)
{
	assert(a);
	int key = a[right];
	int begin = left;
	int end = right - 1;
	while (begin < end)
	{
		while (begin < end && a[begin] <= key)
		{
			++begin;
		}
		while (begin < end && a[end] >= key)
		{
			--end;
		}

		std::swap(a[begin], a[end]);
	}

	if (a[begin] > key)  // 大于key再交換
	{
		std::swap(a[begin], a[right]);
		return begin;
	}
	else
	{
		return right;
	}

}

void QuickSort(int* a, int left, int right)
{
	assert(a);

	if (left < right)
	{
		int pivotloc = Partition(a, left, right);
		QuickSort(a, left, pivotloc-1);
		QuickSort(a, pivotloc+1, right);
	}
}

比較簡單的代碼：（挖坑填數發）

int Partition(int* a, int left, int right)
{
	assert(a);

	int base = a[left];

	while (left < right)
	{
		while (left < right && a[right] >= base)  //注意這里一定要有等于
			--right;							  //否則會有死循環

		a[left] = a[right];

		while (left < right && a[left] <= base)
			++left;

		a[right] = a[left];
	}

	a[left] = base;
	return left;
}

void QuickSort(int* a, int left, int right)
{
	assert(a);

	if (left < right)
	{
		int pivotloc = Partition(a, left, right);
		QuickSort(a, left, pivotloc-1);
		QuickSort(a, pivotloc+1, right);
	}
}

非遞歸寫法：

void QuickSortNoRe(int* a, int left, int right)  //快排非遞歸
{
	assert(a);
	if (left >= right)
		return;

	stack<int> st;
	st.push(right);
	st.push(left);
	while (!st.empty())
	{
		int _left = st.top();
		st.pop();
		int _right = st.top();
		st.pop();
		int mid = Partition(a, _left, _right);

		if (_left < mid - 1)
		{
			st.push(mid - 1);
			st.push(_left);
		}
		if (mid + 1 < _right)
		{
			st.push(_right);
			st.push(mid + 1);
		}
	}
}

性能分析

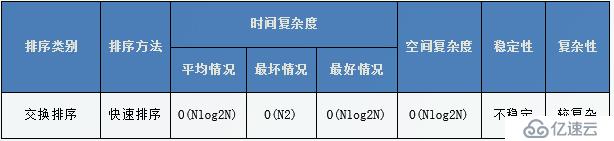
而當數據隨機分布時，以第一個關鍵字為基準分為兩個子序列，兩個子序列的元素

個數接近相等，此時執行效率最好。

當每次遞歸的基準值都是當前區間中最大或者最小的數時，此時效率最差

穩定性

在快速排序中，相等元素可能會因為分區而交換順序，所以它是不穩定的算法。