您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章給大家分享的是一道根據一個整數生成括號對數的題目。文章使用多種方法實現這道題,小編覺得挺實用的,因此分享給大家做個參考。一起跟隨小編過來看看吧。
根據一個整數生成所有的有效的括號組合,這個整數表示括號的對數.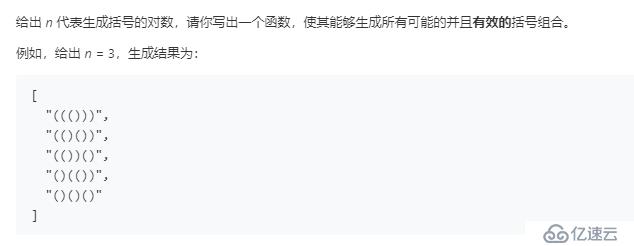
對于n對括號,總共2n個字符,每個字符可以為左括號或右括號,所以總共2^(2n)中組合,暴力法就是枚舉各個組合,然后判斷它們是否為有效的組合:
public void f(char c[],int pos,List<String> result)
{
if(pos == c.length)
{
if(valid(c))
result.add(Arrays.toString(c).replaceAll("(\\[)|(\\])| |,",""));
}
else
{
c[pos] = '(';
f(c,pos+1,result);
c[pos] = ')';
f(c,pos+1,result);
}
}
public boolean valid(char [] f)
{
int len = 0;
for(char c:f)
{
if(c == '(' )
{
if(++len > f.length/2)
return false;
}
else if(len-- <=0)
return false;
}
return len == 0;
}首先加上左括號,進入下一輪遞歸,同時把加括號的位置加1,然后到達2n長度后,判斷是否有效,有效的話加入結果數組,然后回到上一層的遞歸,把當前位置的括號換成右括號,接著再次進入下一輪遞歸,一樣直到2n長度,繼續判斷是否有效,這樣不斷遞歸就會枚舉了所有的組合.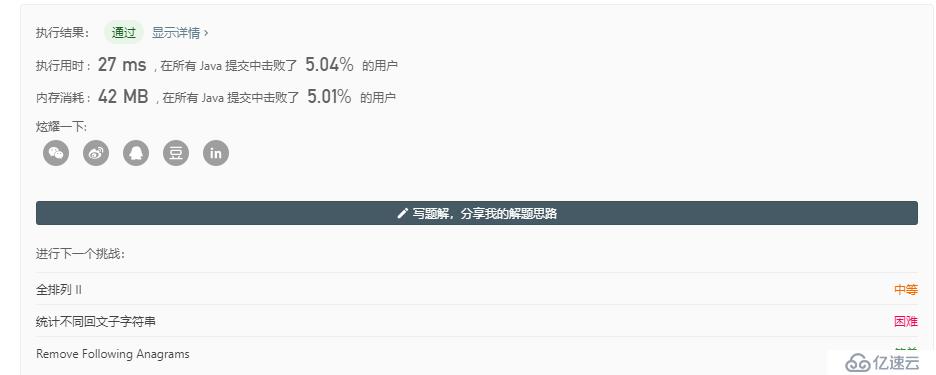
看來不太理想啊.
深搜的話是暴力的改進,暴力的話不管序列是什么狀態都直接添加括號,而深搜的話,當序列有效時才添加括號.
添加左括號的條件:當前的左括號數量小于n.
添加右括號的條件:當前左括號的數量小于右括號的數量.
public void f(String c,int n,int l,int r,List<String> result)
{
if(l == n && r == n)
result.add(c);
else
{
if(l < r)
return ;
if(l < n)
f(c+"(",n,l+1,r,result);
if(r < n)
f(c+")",n,l,r+1,result);
}
}c為上一次遞歸的結果,l,r分別表示左括號與右括號的數量,遞歸的結束條件是左右括號的數量均為n,繼續遞歸的條件是左右括號的數量小于n.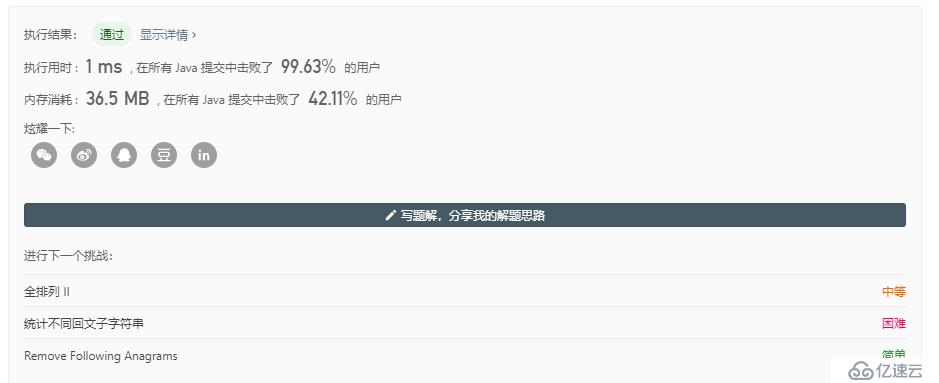
設f(n)表示n對括號的所有有效序列,則有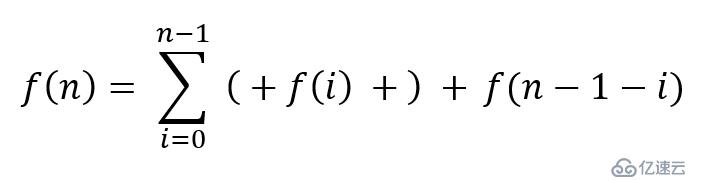
具體來說:
f(3) = ( + f(0) + ) + f(2)
f(3) = ( + f(1) + ) + f(1)
f(3) = ( + f(2) + ) + f(0)這三個都是三對括號的有效序列,因此f(3)最后的結果是這三個有效序列組成的數組.
因為f(n)不一定為一個有效序列,因此返回值為一個數組,剩下的只需要遍歷這個數組,把它們添加到最終結果數組中去:
public List<String> f(int n)
{
List<String> s = new ArrayList<>();
if(n == 0)
s.add("");
for(int i=0;i<n;++i)
{
List<String> l = f(i);
List<String> r = f(n-i-1);
for(String ll:l)
{
for(String rr:r)
{
s.add("("+ll+")"+rr);
}
}
}
return s;
}若n為0,添加一個空序列然后返回,若n不為0,l表示i對括號的所有有效序列,r表示n-i-1對括號的所有有效序列,然后只需要遍歷這兩個序列,在兩邊加上左括號與右括號即可.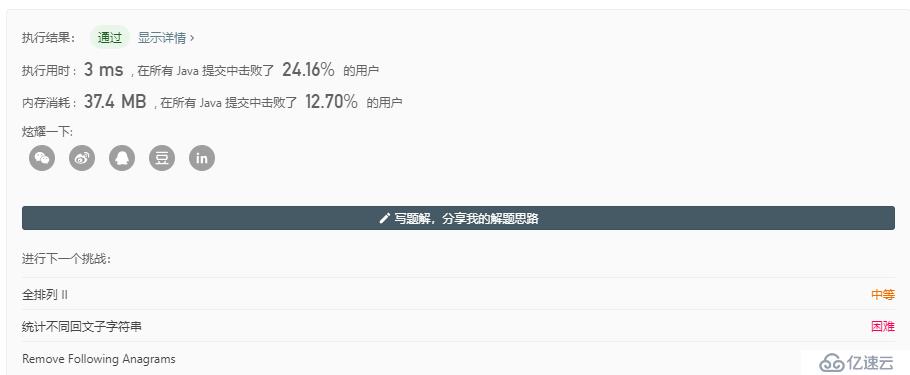
這個...好像沒有深搜快.
上面的遞歸的動規沒有保存之前計算過的結果,比如計算n=3的時候,
f(3) = ( + f(0) + ) + f(2)
f(3) = ( + f(1) + ) + f(1)
f(3) = ( + f(2) + ) + f(0)f(2):
f(2) = ( + f(1) + ) + f(0)
f(2) = ( + f(0) + ) + f(1)f(1)
f(1) = ( + f(0) + ) + f(0)只是計算f(3),計算了
f(2):2次
f(1):2+2*2=6次
f(0):2+2*2+6*2=18次當n增大時,計算的重復度會變得更大,因此可以考慮用一個數組存儲之前計算的結果,需要時直接取出來即可.
public List<String> generateParenthesis(int n)
{
List<List<String>> s = new ArrayList<>();
s.add(Arrays.asList(""));
s.add(Arrays.asList("()"));
for(int n1 = 2;n1<=n;++n1)
{
List<String> t = new ArrayList<>();
for(int i=0;i<n1;++i)
{
List<String> l = s.get(i);
List<String> r = s.get(n1-i-1);
for(String ll:l)
{
for(String rr:r)
{
t.add("("+ll+")"+rr);
}
}
}
s.add(t);
}
return s.get(n);
}可以先看最后的return,因為s保存了0到n的所有結果,所以,直接get即可.
然后設置一個臨時的n1,表示當前要計算的n1對括號的序列,當n1增加時,表示已經完成了計算n1對括號的序列,t為結果,添加到s中去.直到n1與n相等,計算完最后一個n1后,直接返回s的最后一個序列.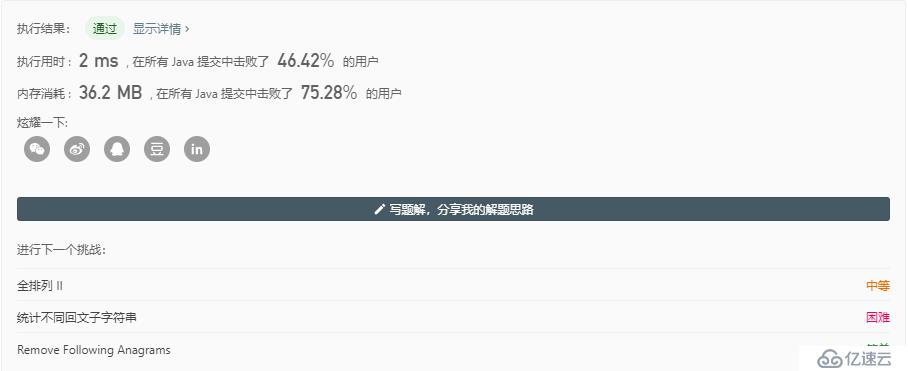
嗯,快了1ms,看來優化還是有效果的.
關于根據一個整數生成括號對數的方法就分享到這里了,希望以上內容可以對大家有一定的幫助,可以學到更多知識。如果喜歡這篇文章,不如把它分享出去讓更多的人看到。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。