淺析STL算法中的堆排序

堆結構簡述

    了解過數據結構的人，應該對堆結構不陌生，堆的底層是使用數組來實現的，但卻保持了二叉樹的特性。堆分為兩種，最大堆和最小堆，以最大堆為例，最大堆保持了根結點大于兩個左右兩個孩子，同時所有子樹一次類推。由于堆底層是數組結構，這里從跟結點開始，按照層序依次走到最后一個結點，結點下標分貝為0~N-1。結構如下圖：

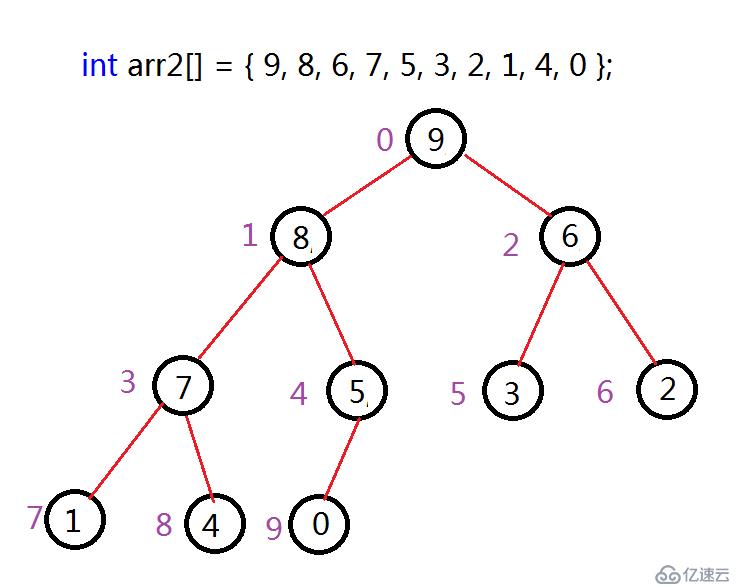
    上圖中，紫色表示的是該元素在數組中的下標，可以看到，每個結點的值總是大于它的左右孩子，這里并沒有規定左右孩子的大小關系，也沒有規定不是同一棵樹之間結點的大小關系。這就是最大堆。同時這里可以注意到，如果是大堆，根節點一定是樹中最大的結點，同樣，如果是小堆，根節點一定是樹中最小的結點。

    堆結構在排序領域，占據著一定的低位，但是STL中并沒有直接給出堆結構，而是把堆的相關算法，寫在了 algorithm 里面。在這里我不會過多的去模擬實現一個堆，今天要說的是關于STL中給出的堆算法如何使用。

algorithm 中的堆算法

    在STL中，關于堆，給出了一下幾種算法。

    ★make_heap    

    ★push_heap

    ★pop_heap

    ★sort_heap

    這里，首先給出一個利用STL中堆算法的實例

#include <algorithm>
#include <vector>
void test()
{
    int arr[] = {1,2,3,4,5,6,7};
    vector<int> vec(arr, arr+7);         // 左開右閉類型
    make_heap(vec.begin(), vec.end());   // 默認建大堆
    pop_heap(v1.begin(), v1.end());      
    v1.pop_back();                       
    sort_heap(vec.begin(), vec.end());   // 堆排序
    for(size_t i = 0; i < vec.size(); i++)
        cout<<vec[i]<<" ";
    cout<<endl;
}

    上面代碼，首先用一個數組構建了一個向量，之后對向量vec建堆，pop出調整之后的向量中第一個元素，并進行調整，然后進行堆排序，最后將結果打印出來，打印結果如下：

    看完了heap算法的基本使用，現在，我們了解一下，STL中是如何提供這些算法接口的。

1、make_heap

template <class RandomAccessIterator>
  void make_heap (RandomAccessIterator first, RandomAccessIterator last);

template <class RandomAccessIterator, class Compare>
  void make_heap (RandomAccessIterator first, RandomAccessIterator last,
                  Compare comp );

    前面提到過，堆分為大堆和小堆，我們建立堆的時候就需要確定，但剛剛例子中，我們并沒有去指定大小堆。STL中規定，沒有指定的話，默認大堆結構。從上面關于make_heap的兩套接口可以看到，第一種是默認的，沒有提供指定大小堆的接口，第二種這里有實現。我們可通過仿函數的結構，實現這里的傳參。

    對剛剛給出的例子，我們現在可以解釋另外一個問題，為什么我們要進行堆排序，首先要構建vector呢？因為堆的底層實現就是通過數組的形式，而vector是堆數組的高級封裝，這些庫中實現好的容器給出了很多實用的接口和迭代器，使用起來的確可以方便不少。make_heap給出的接口中，前兩個是任意類型的迭代器（當然，這里也可以直接傳遞數組的指針），不論是make_heap還是其他三個函數，這里的迭代器區間總是左閉右開的，這是個需要注意的地方。

    接下來我們來介紹仿函數這里的實現。還是上面的例子，如何讓上面剪子一個最小堆呢？

//仿函數結構：

struct Compare
{
   bool operator()(int num1, int num2)
	           {
		      return num1 > num2;
	   }
};

// 建堆時，參數傳遞改為

make_heap(vec.begin(), vec.end() , Compare());   // 建小堆

    注意，上面我寫的是num1 > num2，這樣建出來頂點是小堆。關于make_heap就說到這里。

2、push_heap 與 pop_heap 

    push表示的是向vector中插入一個元素，但這里它并不是直接插入元素，準確的說，它的功能只是做調整，在push_heap之前，首先需要調用vec.push_back(x)，向vector尾部插入一個元素，然后在調用push_heap函數進行調整，使得整個樹重新滿足堆結構。

    pop_heap與push_heap類似，同樣沒有直接改變vector中元素個數的能力。對于堆而言，pop要做的是將vector的第一個元素扔出去，為了不直接破壞樹的結構，這里先調用pop_heap函數，將堆中的最大值或最小值放到vector的尾部，同時進行一次調整，使得堆結構依然成立，然后調用vec.pop+back()函數，將最后一個元素從vector中剔除。

    這就是插入和刪除的整個過程。

3、sort_heap

    顧名思義，sort_heap就是進行堆排序的意思，對堆結構進行排序，得到的結果就是vector中的元素變得有序。這里，構建大堆，排序結果是升序的，構建小堆，得到的排序結果是降序的。

    上面就是關于堆排序的基本算法，關于C++11新引入的兩個函數，這里不做討論。

    關于STL中的堆結構，這里有幾點還是需要注意的：

    1、因為堆結構，是建立在vector上的結構，所以如果要進行堆排序，整個過程中至少一次建堆（make_heap）的過程。

    2、當建堆完成之后，如果再向vector中插入元素，需要調用 push_heap(v1.begin(), v1.end()) 進行一次向上調整；如果從vector中Pop出一個元素，需要調用 pop_heap(v1.begin(), v1.end()) 進行一次向下調整。

    如果沒有調整，當調用 sort_heap(v1.begin(), v1.end()) 函數的過程中，會出現由于堆不合法引起的斷言錯誤。

    3、不可以讓vector多次尾插，之后再多次向上調整，會造成堆混亂，排序時也會出現斷言錯誤。當然，多次插入或刪除之后，可以再次進行重新建堆，只不過消耗的時間代價會比較大。

堆結構實際應用

接下來，看一道面試題：

CVTE：統計公司員工最喜歡吃的前K種水果

   有過上面的基礎，我這里直接給出demo

#include <algorithm>
#include <map>
#include <string>
#include <vector>

struct Min
{
            bool operator()(pair<string, int> p1, pair<string, int> p2)
            {
                        return p1.second > p2.second;
            }
};
void HeapSort()
{
            vector<string> v1 = { "蘋果", "香蕉", "蘋果"
                        , "蘋果", "蘋果", "香蕉"
                        , "蘋果", "獼猴桃", "草莓" };
            map<string, int> fruit;
            
            //用map統計次數
            for (size_t i = 0; i < v1.size(); i++)
            {
                        fruit[v1[i]]++;
            }

            // 用heap排序
            vector<pair<string, int>> vec;
            map<string, int>::iterator it = fruit.begin();
            //while (it != fruit.end())
            //{
            //         vec.push_back(pair<string, int>(it->first, it->second));
            //         it++;
            //}
            vec.insert(vec.begin(), fruit.begin(), fruit.end());
            make_heap(vec.begin(), vec.end(), Min());
            sort_heap(vec.begin(), vec.end(), Min());
            int K = 3;
            for (size_t i = 0; (i < K) && (i < vec.size()); i++)
            {
                        cout << vec[i].first <<"--"<<vec[i].second<< endl;
            }
}
int main()
{
            HeapSort();
            system("pause");
            return 0;
}

    堆排序是數據結構中一塊很重要的內容，如果是在實際開發中，更加推薦的是熟悉STL中給出的算法，正如上文講到的內容。如果是對于初學者，這里還是推薦對堆結構和算法的底層實現有一個更加深刻的認識，對于堆的調整算法，不可否認，是數據結構中較為重要的一部分。下一次，會對堆結構進行模擬實現，更加深入地了解底層結構。