您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“NumPy矩陣向量線性代數的操作方法有哪些”,在日常操作中,相信很多人在NumPy矩陣向量線性代數的操作方法有哪些問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”NumPy矩陣向量線性代數的操作方法有哪些”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
在NumPy中,矩陣可以看作是一個二維數組,其中每個元素都可以通過行列坐標來定位。它表示為一個m×n的矩形網格,其中m表示矩陣的行數,n表示矩陣的列數。在計算機科學中,矩陣通常用數字或符號表示,并且可以進行加、減、乘等運算。
一個M X N的矩陣是一個由M行(row)N列(column)元素排列成的矩形陣列。矩陣里的元素可以是數字、符號或數學式。
以下是一個由 6 個數字元素構成的 2 行 3 列的矩陣:
[1 2 3] [4 5 6]
注意:2×3矩陣即2行3列,請把左、右兩邊的多個[與多個]看成一個整體[]
在 NumPy 中,向量是一維數組對象,其所有元素都必須具有相同的數據類型。向量可以通過創建一個一維數組來實現。
向量是一種特殊的矩陣,其中只包含一行或一列元素。向量通常用數字或符號表示,其大小表示向量包含的元素數量。
創建一個包含五個元素的向量:
import numpy as np v = np.array([1, 2, 3, 4, 5])
import numpy as np # 創建一維數組 v = np.array([1, 2, 3]) print(v) # 輸出:[1 2 3]
import numpy as np # 創建二維數組 m = np.array([[1, 2, 3], [4, 5, 6]]) print(m) # 輸出:[[1 2 3] # [4 5 6]]
import numpy as np # 創建一維數組 v = np.array([1, 2, 3]) # 訪問元素 print(v[0]) # 輸出:1 print(v[1]) # 輸出:2 print(v[2]) # 輸出:3
NumPy中除了可以使用numpy.transpose 函數來對換數組的維度,還可以使用 T 屬性。
例如有個 m 行 n 列的矩陣,使用 t() 函數就能轉換為 n 行 m 列的矩陣。
import numpy as np # 創建矩陣 A = np.array([[1, 2], [3, 4]]) # 轉置矩陣 AT = np.transpose(A) print(AT) # 輸出:[[1 3] # [2 4]] print (A.T)
# 矩陣加法 np.add(A, B) # 矩陣減法 np.subtract(A, B) # 矩陣乘法 # 在進行矩陣乘法時,前一個矩陣的列數必須等于后一個矩陣的行數,才能進行乘法運算 # (M行, N列)*(N行, L列) = (M行, L列) p.dot(A, B) # 矩陣除法 np.divide(A, B)
import numpy as np
# 創建矩陣A和B
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
print("A + B:")
print(np.add(A, B))
[1, 2] [5, 6] [6, 8]
+ =
[3, 4] [7, 8] [10, 12]
print("A - B:")
print(np.subtract(A, B))
[1, 2] [5, 6] [-4, -4]
- =
[3, 4] [7, 8] [-4, -4]
print("A * B:")
print(np.dot(A, B))
[1, 2] [5, 6] [19, 22]
* =
[3, 4] [7, 8] [43, 50]
print("A / B:")
print(np.divide(A, B))
[1, 2] [5, 6] [0.2, 0.33333333]
/ =
[3, 4] [7, 8] [0.42857143, 0.5]矩陣和矩陣(向量)相乘: (M行, N列)*(N行, L列) = (M行, L列)
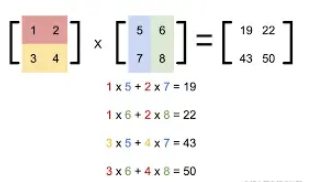
m×n 的矩陣乘以 n×1 的向量,得到的是 m×1 的向量
[1, 2] [1] [19] * = [3, 4] [1] [43]
使用numpy.linalg.inv()函數進行矩陣求逆操作
import numpy as np # 創建矩陣 matrix = np.array([[1, 2], [3, 4]]) # 求逆矩陣 result = np.linalg.inv(matrix) print(result)
使用numpy.trace()函數可以計算矩陣的跡
import numpy as np # 創建矩陣 matrix = np.array([[1, 2], [3, 4]]) # 計算矩陣的跡 result = np.trace(matrix) print(result)
使用numpy.dot()函數進行向量點積操作
import numpy as np # 創建兩個向量 vector1 = np.array([1, 2]) vector2 = np.array([3, 4]) # 向量點積 result = np.dot(vector1, vector2) print(result)
使用numpy.linalg.norm()函數可以計算向量的范數
import numpy as np # 創建向量 vector = np.array([1, 2, 3]) # 計算向量的L2范數 result = np.linalg.norm(vector) print(result)
NumPy的線性代數模塊(numpy.linalg)提供了許多矩陣運算函數,如矩陣乘法、求逆、行列式、特征值等,該庫包含了線性代數所需的所有功能。
常用的 NumPy 線性代數函數:
| 函數 | 說明 |
|---|---|
| np.dot(a, b): | 兩個數組的點積,即元素對應相乘 |
| np.matmul(a, b) | 兩個數組的矩陣積 |
| np.linalg.inv(a) | 計算矩陣的逆 |
| np.linalg.det(a) | 計算矩陣的行列式 |
| np.linalg.eig(a) | 計算矩陣的特征值和特征向量 |
| np.linalg.solve(a, b) | 解線性方程組 ax=b |
import numpy as np a = np.array([[1, 2], [3, 4]]) b = np.array([[5, 6], [7, 8]]) print(np.dot(a, b)) # [[19 22] # [43 50]]
import numpy as np a = np.array([[1, 2], [3, 4]]) print(np.linalg.inv(a)) # [[-2. 1. ] # [ 1.5 -0.5]]
import numpy as np a = np.array([[2, 3], [4, 5]]) b = np.array([5, 6]) x = np.linalg.solve(a, b) print(x) # [-4. 5.]
解得的線性方程組如下,其解為x1=−4,x2=5

到此,關于“NumPy矩陣向量線性代數的操作方法有哪些”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。