Python實現概率分布公式及數據可視化的方法有哪些

這篇文章主要介紹了Python實現概率分布公式及數據可視化的方法有哪些的相關知識，內容詳細易懂，操作簡單快捷，具有一定借鑒價值，相信大家閱讀完這篇Python實現概率分布公式及數據可視化的方法有哪些文章都會有所收獲，下面我們一起來看看吧。

現實世界中有幾個現象實例被認為是統計性質的（即天氣數據、銷售數據、財務數據等）。這意味著在某些情況下，我們已經能夠開發出方法來幫助我們通過可以描述數據特征的數學函數來模擬自然。“概率分布是一個數學函數，它給出了實驗中不同可能結果的發生概率。”了解數據的分布有助于更好地模擬我們周圍的世界。它可以幫助我們確定各種結果的可能性，或估計事件的可變性。所有這些都使得了解不同的概率分布在數據科學和機器學習中非常有價值。均勻分布最直接的分布是均勻分布。均勻分布是一種概率分布，其中所有結果的可能性均等。例如，如果我們擲一個公平的骰子，落在任何數字上的概率是 1/6。這是一個離散的均勻分布。但是并不是所有的均勻分布都是離散的——它們也可以是連續的。它們可以在指定范圍內取任何實際值。a 和 b 之間連續均勻分布的概率密度函數 (PDF) 如下：讓我們看看如何在 Python 中對它們進行編碼：

import numpy as np
import matplotlib.pyplot as plt 
from scipy import stats 
 
# for continuous
a = 0 
b = 50 
size = 5000 
 
X_continuous = np.linspace(a, b, size) 
continuous_uniform = stats.uniform(loc=a, scale=b) 
continuous_uniform_pdf = continuous_uniform.pdf(X_continuous) 
 
# for discrete 
X_discrete = np.arange(1, 7) 
discrete_uniform = stats.randint(1, 7) 
discrete_uniform_pmf = discrete_uniform.pmf(X_discrete)
 
# plot both tables 
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15,5)) 
# discrete plot 
ax[0].bar(X_discrete, discrete_uniform_pmf) 
ax[0].set_xlabel("X") 
ax[0].set_ylabel("Probability") 
ax[0].set_title("Discrete Uniform Distribution") 
# continuous plot 
ax[1].plot(X_continuous, continuous_uniform_pdf) 
ax[1].set_xlabel("X") 
ax[1].set_ylabel("Probability") 
ax[1].set_title("Continuous Uniform Distribution") 
plt.show()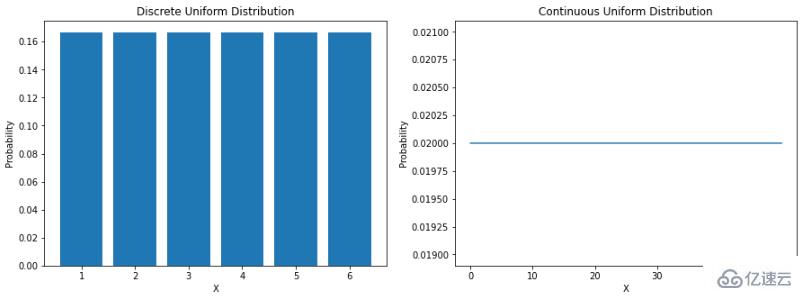

高斯分布

高斯分布可能是最常聽到也熟悉的分布。它有幾個名字：有人稱它為鐘形曲線，因為它的概率圖看起來像一個鐘形，有人稱它為高斯分布，因為首先描述它的德國數學家卡爾·高斯命名，還有一些人稱它為正態分布，因為早期的統計學家 注意到它一遍又一遍地再次發生。正態分布的概率密度函數如下：σ 是標準偏差，μ 是分布的平均值。要注意的是，在正態分布中，均值、眾數和中位數都是相等的。當我們繪制正態分布的隨機變量時，曲線圍繞均值對稱——一半的值在中心的左側，一半在中心的右側。并且，曲線下的總面積為 1。

mu = 0 
variance = 1 
sigma = np.sqrt(variance) 
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100) 
 
plt.subplots(figsize=(8, 5)) 
plt.plot(x, stats.norm.pdf(x, mu, sigma)) 
plt.title("Normal Distribution") 
plt.show()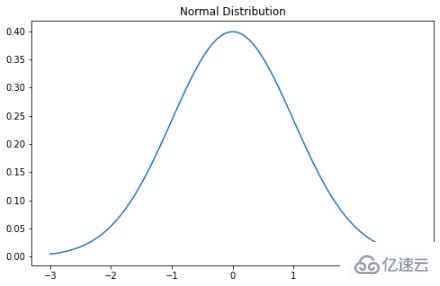

對于正態分布來說。經驗規則告訴我們數據的百分比落在平均值的一定數量的標準偏差內。這些百分比是：

• 68% 的數據落在平均值的一個標準差內。

• 95% 的數據落在平均值的兩個標準差內。

• 99.7% 的數據落在平均值的三個標準差范圍內。

對數正態分布

對數正態分布是對數呈正態分布的隨機變量的連續概率分布。因此，如果隨機變量 X 是對數正態分布的，則 Y = ln(X) 具有正態分布。這是對數正態分布的 PDF：對數正態分布的隨機變量只取正實數值。因此，對數正態分布會創建右偏曲線。讓我們在 Python 中繪制它：

X = np.linspace(0, 6, 500) 
 
std = 1 
mean = 0 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
 
fig, ax = plt.subplots(figsize=(8, 5)) 
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=1") 
ax.set_xticks(np.arange(min(X), max(X))) 
 
std = 0.5 
mean = 0 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=0.5") 
 
std = 1.5 
mean = 1 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
plt.plot(X, lognorm_distribution_pdf, label="μ=1, σ=1.5") 
 
plt.title("Lognormal Distribution") 
plt.legend() 
plt.show()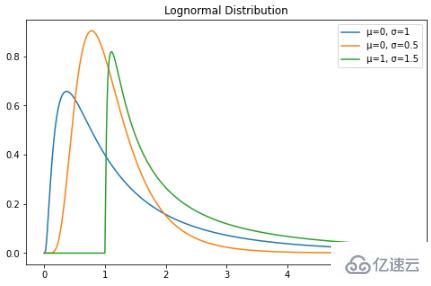

泊松分布

泊松分布以法國數學家西蒙·丹尼斯·泊松的名字命名。這是一個離散的概率分布，這意味著它計算具有有限結果的事件——換句話說，它是一個計數分布。因此，泊松分布用于顯示事件在指定時期內可能發生的次數。如果一個事件在時間上以固定的速率發生，那么及時觀察到事件的數量（n）的概率可以用泊松分布來描述。例如，顧客可能以每分鐘 3 次的平均速度到達咖啡館。我們可以使用泊松分布來計算 9 個客戶在 2 分鐘內到達的概率。下面是概率質量函數公式：λ 是一個時間單位的事件率——在我們的例子中，它是 3。k 是出現的次數——在我們的例子中，它是 9。這里可以使用 Scipy 來完成概率的計算。

from scipy import stats 

print(stats.poisson.pmf(k=9, mu=3))

0.002700503931560479

泊松分布的曲線類似于正態分布，λ 表示峰值。

X = stats.poisson.rvs(mu=3, size=500) 
 
plt.subplots(figsize=(8, 5)) 
plt.hist(X, density=True, edgecolor="black") 
plt.title("Poisson Distribution") 
plt.show()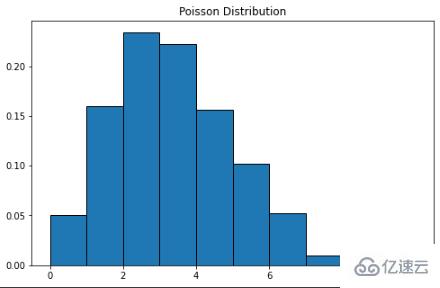

指數分布

指數分布是泊松點過程中事件之間時間的概率分布。指數分布的概率密度函數如下：λ 是速率參數，x 是隨機變量。

X = np.linspace(0, 5, 5000) 
 
exponetial_distribtuion = stats.expon.pdf(X, loc=0, scale=1) 
 
plt.subplots(figsize=(8,5)) 
plt.plot(X, exponetial_distribtuion) 
plt.title("Exponential Distribution") 
plt.show()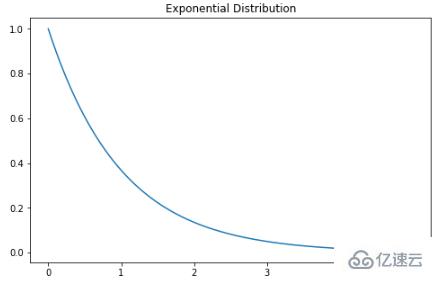

二項分布

可以將二項分布視為實驗中成功或失敗的概率。有些人也可能將其描述為拋硬幣概率。參數為 n 和 p 的二項式分布是在 n 個獨立實驗序列中成功次數的離散概率分布，每個實驗都問一個是 - 否問題，每個實驗都有自己的布爾值結果：成功或失敗。本質上，二項分布測量兩個事件的概率。一個事件發生的概率為 p，另一事件發生的概率為 1-p。這是二項分布的公式：

• P = 二項分布概率

• = 組合數

• x = n次試驗中特定結果的次數

• p = 單次實驗中，成功的概率

• q = 單次實驗中，失敗的概率

• n = 實驗的次數

可視化代碼如下：

X = np.random.binomial(n=1, p=0.5, size=1000) 
 
plt.subplots(figsize=(8, 5)) 
plt.hist(X) 
plt.title("Binomial Distribution") 
plt.show()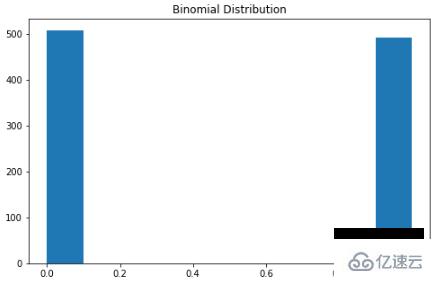

學生 t 分布

學生 t 分布（或簡稱 t 分布）是在樣本量較小且總體標準差未知的情況下估計正態分布總體的均值時出現的連續概率分布族的任何成員。它是由英國統計學家威廉·西利·戈塞特（William Sealy Gosset）以筆名“student”開發的。PDF如下：n 是稱為“自由度”的參數，有時可以看到它被稱為“d.o.f.” 對于較高的 n 值，t 分布更接近正態分布。

import seaborn as sns 
from scipy import stats 
 
X1 = stats.t.rvs(df=1, size=4) 
X2 = stats.t.rvs(df=3, size=4) 
X3 = stats.t.rvs(df=9, size=4) 
 
plt.subplots(figsize=(8,5)) 
sns.kdeplot(X1, label = "1 d.o.f") 
sns.kdeplot(X2, label = "3 d.o.f") 
sns.kdeplot(X3, label = "6 d.o.f") 
plt.title("Student's t distribution") 
plt.legend() 
plt.show()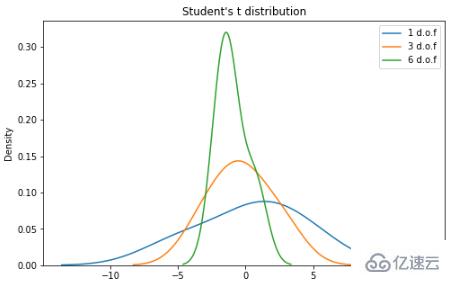

卡方分布

卡方分布是伽馬分布的一個特例；對于 k 個自由度，卡方分布是一些獨立的標準正態隨機變量的 k 的平方和。PDF如下：這是一種流行的概率分布，常用于假設檢驗和置信區間的構建。在 Python 中繪制一些示例圖：

X = np.arange(0, 6, 0.25) 
 
plt.subplots(figsize=(8, 5)) 
plt.plot(X, stats.chi2.pdf(X, df=1), label="1 d.o.f") 
plt.plot(X, stats.chi2.pdf(X, df=2), label="2 d.o.f") 
plt.plot(X, stats.chi2.pdf(X, df=3), label="3 d.o.f") 
plt.title("Chi-squared Distribution") 
plt.legend() 
plt.show()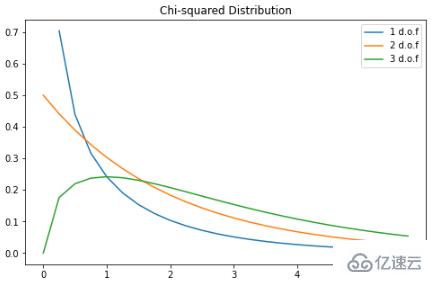

關于“Python實現概率分布公式及數據可視化的方法有哪些”這篇文章的內容就介紹到這里，感謝各位的閱讀！相信大家對“Python實現概率分布公式及數據可視化的方法有哪些”知識都有一定的了解，大家如果還想學習更多知識，歡迎關注億速云行業資訊頻道。