Matlab計算變異函數并繪制經驗半方差圖的方法是什么

這篇“Matlab計算變異函數并繪制經驗半方差圖的方法是什么”文章的知識點大部分人都不太理解，所以小編給大家總結了以下內容，內容詳細，步驟清晰，具有一定的借鑒價值，希望大家閱讀完這篇文章能有所收獲，下面我們一起來看看這篇“Matlab計算變異函數并繪制經驗半方差圖的方法是什么”文章吧。

1 數據處理

1.1 數據讀取

本文中，我的初始數據為某區域658個土壤采樣點的空間位置（X與Y，單位為米）、pH值、有機質含量與全氮含量。這些數據均存儲于data.xls文件中；而后期操作多于MATLAB軟件中進行。因此，首先需將源數據選擇性地導入MATLAB軟件中。

利用MATLAB軟件中xlsread函數可以實現這一功能。具體代碼附于本文的1.3 正態分布檢驗及轉換處。

1.2 異常數據剔除

得到的采樣點數據由于采樣記錄、實驗室測試等過程，可能具有一定誤差，從而出現個別異常值。選用平均值加標準差法對這些異常數據加以篩選、剔除。

分別利用平均值加標準差法中“2S”與“3S”方法加以處理，發現“2S”方法處理效果相對后者較好，故后續實驗取“2S”方法處理結果繼續進行。

其中，“2S”方法是指將數值大于或小于其平均值±2倍標準差的部分視作異常值，“3S”方法則是指將數值大于或小于其平均值±3倍標準差的部分視作異常值。

得到異常值后，將其從658個采樣點中剔除；剩余的采樣點數據繼續后續操作。

本部分具體代碼附于1.3 正態分布檢驗及轉換處。

1.3 正態分布檢驗及轉換

計算變異函數需建立在初始數據符合正態分布的假設之上；而采樣點數據并不一定符合正態分布。因此，我們需要對原始數據加以正態分布檢驗。

一般地，正態分布檢驗可以通過數值檢驗與直方圖、QQ圖等圖像加以直觀判斷。本文綜合采取以上兩種數值、圖像檢驗方法，共同判斷正態分布特性。

針對數值檢驗方法，我在一開始準備選擇采用Kolmogorov-Smirnov檢驗方法；但由于了解到，這一方法僅僅適用于標準正態檢驗，因此隨后改用Lilliefors檢驗。

Kolmogorov-Smirnov檢驗通過樣本的經驗分布函數與給定分布函數的比較，推斷該樣本是否來自給定分布函數的總體；當其用于正態性檢驗時只能做標準正態檢驗。

Lilliefors檢驗則將上述Kolmogorov-Smirnov檢驗改進，其可用于一般的正態分布檢驗。

QQ圖（Quantile Quantile Plot）是一種散點圖，其橫坐標表示某一樣本數據的分位數，縱坐標則表示另一樣本數據的分位數；橫坐標與縱坐標組成的散點圖代表同一個累計概率所對應的分位數。

因此，QQ圖具有這樣的特點：針對y=x這一直線，若散點圖中各點均在直線附近分布，則說明兩個樣本為同等分布；因此，若將橫坐標（縱坐標）表示為一個標準正態分布樣本的分位數，則散點圖中各點均在上述直線附近分布可以說明，縱坐標（橫坐標）表示的樣本符合或基本近似符合正態分布。本文采用將橫坐標表示為正態分布的方式。

此外，PP圖（Probability Probability Plot）同樣可以用于正態分布的檢驗。PP圖橫坐標表示某一樣本數據的累積概率，縱坐標則表示另一樣本數據的累積概率；其根據變量的累積概率對應于所指定的理論分布累積概率并繪制的散點圖，用于直觀地檢測樣本數據是否符合某一概率分布。和QQ圖類似，如果被檢驗的數據符合所指定的分布，則其各點均在上述直線附近分布。若將橫坐標（縱坐標）表示為一個標準正態分布樣本的分位數，則散點圖中各點均在直線附近分布可以說明，縱坐標（橫坐標）表示的樣本符合或基本近似符合正態分布。

三種土壤屬性，我選擇首先以pH數值為例進行操作。通過上述數值檢驗、圖像檢驗方法，檢驗得到剔除異常值后的原始pH數值數據并不符合正態分布這一結論。因此，嘗試對原數據加以對數、開平方等轉換處理；隨后發現，原始pH值開平方數據的正態分布特征雖然依舊無法通過較為嚴格的Lilliefors檢驗，但其直方圖、QQ圖的圖像檢驗結果較為接近正態分布，并較之前二者更加明顯。故后續取開平方處理結果繼續進行。

值得一提的是，本文后半部分得到pH值開平方數據的實驗變異函數及其散點圖后，在對其余兩種空間屬性數據（即有機質含量與全氮含量）進行同樣的操作時，發現全氮含量數據在經過“2S”方法剔除異常值后，其原始形式的數據是可以通過Lilliefors檢驗的，且其直方圖、QQ圖分布特點十分接近正態分布。

我亦準備嘗試對空間屬性數據進行反正弦轉換。但隨后發現，已有三種屬性數值的原始數據并不嚴格分布在-1至1的區間內，因此并未對其進行反正弦方式的轉換。

經過上述檢驗、轉換處理過后的圖像檢驗結果如下所示。

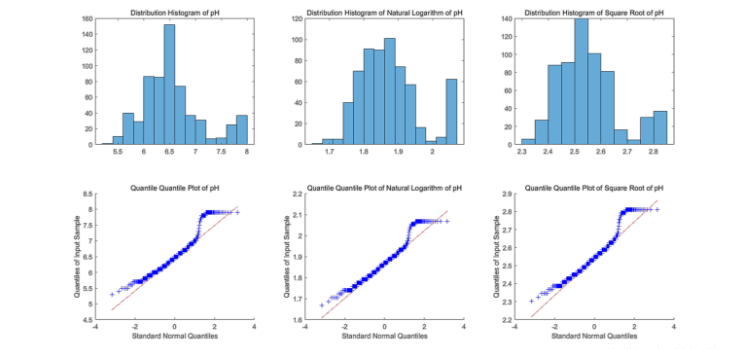
以上部分代碼如下：

clc;clear;
info=xlsread('data.xls');
oPH=info(:,3);
oOM=info(:,4);
oTN=info(:,5);
 
mPH=mean(oPH);
sPH=std(oPH);
num2=find(oPH>(mPH+2*sPH)|oPH<(mPH-2*sPH));
num3=find(oPH>(mPH+3*sPH)|oPH<(mPH-3*sPH));
PH=oPH;
for i=1:length(num2)
    n=num2(i,1);
    PH(n,:)=[0];
end
PH(all(PH==0,2),:)=[];
 
%KSTest(PH,0.05)
H1=lillietest(PH);
 
for i=1:length(PH)
    lPH(i,:)=log(PH(i,:));
end
 
H2=lillietest(lPH);
 
for i=1:length(PH)
    sqPH(i,:)=(PH(i,:))^0.5;
end
 
H3=lillietest(sqPH);
 
% for i=1:length(PH)
%     arcPH(i,:)=asin(PH(i,:));
% end
% 
% H4=lillietest(arcPH);
 
subplot(2,3,1),histogram(PH),title("Distribution Histogram of pH");
subplot(2,3,2),histogram(lPH),title("Distribution Histogram of Natural Logarithm of pH");
subplot(2,3,3),histogram(sqPH),title("Distributio n Histogram of Square Root of pH");
subplot(2,3,4),qqplot(PH),title("Quantile Quantile Plot of pH");
subplot(2,3,5),qqplot(lPH),title("Quantile Quantile Plot of Natural Logarithm of pH");
subplot(2,3,6),qqplot(sqPH),title("Quantile Quantile Plot of Square Root of pH");

2 距離量算

接下來，需要對篩選出的采樣點相互之間的距離加以量算。這是一個復雜的過程，需要借助循環語句。

本部分具體代碼如下。

poX=info(:,1);
poY=info(:,2);
dis=zeros(length(PH),length(PH));
for i=1:length(PH)
    for j=i+1:length(PH)
        dis(i,j)=sqrt((poX(i,1)-poX(j,1))^2+(poY(i,1)-poY(j,1))^2);
    end
end

3 距離分組

計算得到全部采樣點相互之間的距離后，我們需要依據一定的范圍劃定原則，對距離數值加以分組。

距離分組首先需要確定步長。經過實驗發現，若將步長選取過大會導致得到的散點圖精度較低，而若步長選取過小則可能會使得每組點對總數量較少。因此，這里取步長為500米；其次確定最大滯后距，這里以全部采樣點間最大距離的一半為其值。隨后計算各組對應的滯后級別、各組上下界范圍等。

本部分具體代碼附于本文4 平均距離、半方差計算及其繪圖處。

4 平均距離、半方差計算及其繪圖

分別計算各個組內對應的點對個數、點對間距離總和以及點對間屬性值差值總和等。隨后，依據上述參數，最終求出點對間距離平均值以及點對間屬性值差值平均值。

依據各組對應點對間距離平均值為橫軸，各組對應點對間屬性值差值平均值為縱軸，繪制出經驗半方差圖。

本部分及上述部分具體代碼如下。

madi=max(max(dis));
midi=min(min(dis(dis>0)));
radi=madi-midi;
ste=500;
clnu=floor((madi/2)/ste)+1;
ponu=zeros(clnu,1);
todi=ponu;
todiav=todi;
diff=ponu;
diffav=diff;
for k=1:clnu
    midite=ste*(k-1);
    madite=ste*k;
    for i=1:length(sqPH)
        for j=i+1:length(sqPH)
            if dis(i,j)>midite && dis(i,j)<=madite
                ponu(k,1)=ponu(k,1)+1;
                todi(k,1)=todi(k,1)+dis(i,j); diff(k,1)=diff(k,1)+(sqPH(i)-sqPH(j))^2;
            end
        end
    end
    todiav(k,1)=todi(k,1)/ponu(k,1);
    diffav(k,1)=diff(k,1)/ponu(k,1)/2;
end
plot(todiav(:,1),diffav(:,1)),title("Empirical Semivariogram of Square Root of pH");
xlabel("Separation Distance (Metre)"),ylabel("Standardized Semivariance");

5 繪圖結果

通過上述過程，得到pH值開平方后的實驗變異函數折線圖及散點圖。

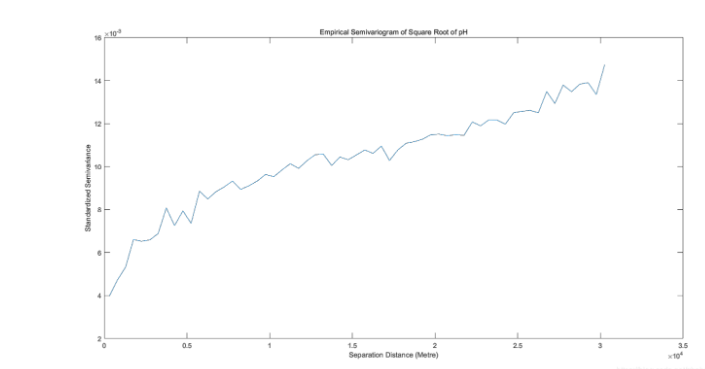
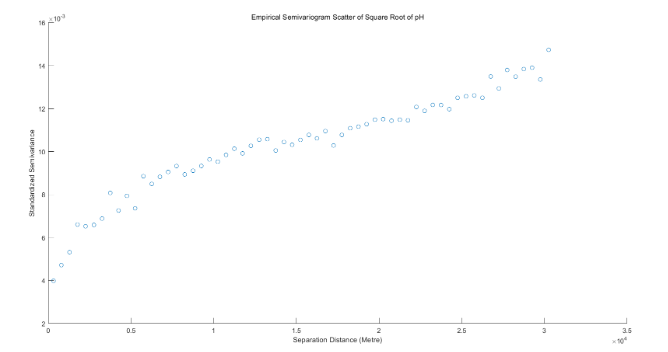
可以看到，pH值開平方后的實驗變異函數較符合于有基臺值的球狀模型或指數模型。函數數值在距離為0至8000米區間內快速上升，在距離為8000米后數值上升放緩，變程為25000米左右；即其“先快速上升，再增速減緩，后趨于平穩”的圖像整體趨勢較為明顯。但其數值整體表現較低——塊金常數為0.004左右，而基臺值僅為0.013左右。為驗證數值正確性，同樣對有機質、全氮進行上述全程操作。

得到二者對應變異函數折線圖與散點圖。

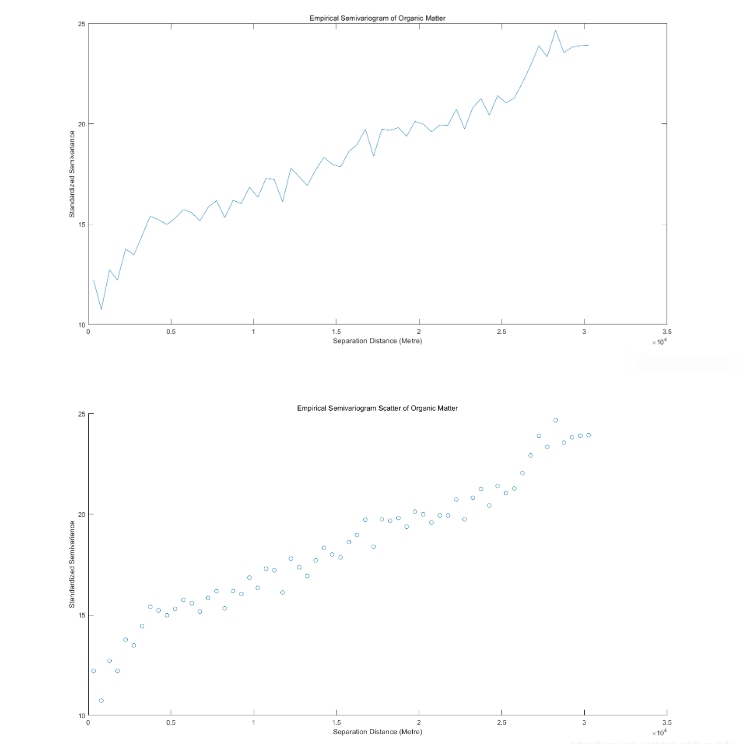
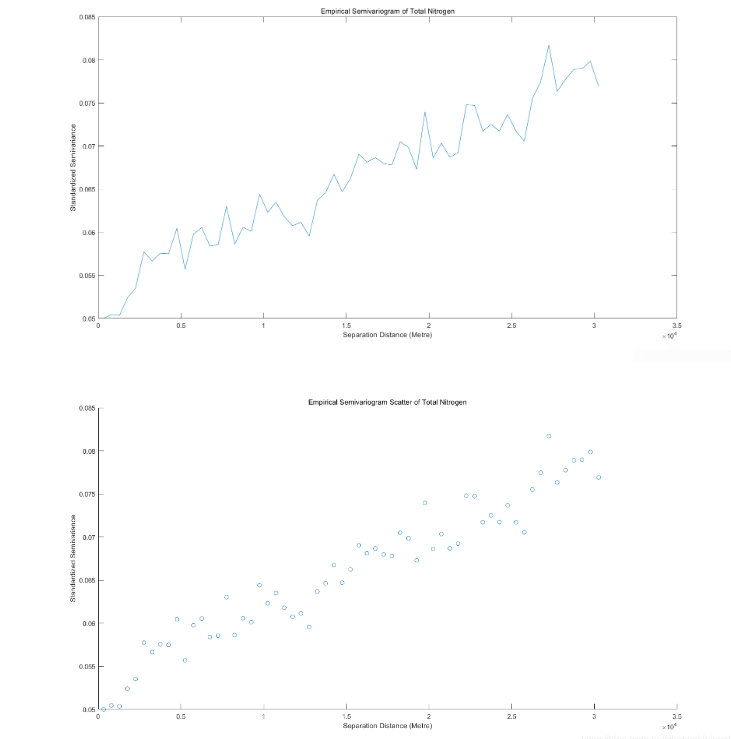
由以上三組、共計六幅的pH值開平方、有機質與全氮對應的實驗變異函數折線圖與散點圖可知，不同數值對應實驗變異函數數值的數量級亦會有所不同；但其整體“先快速上升，再增速減緩，后趨于平穩”的圖像整體趨勢是十分一致的。

此外，如上文所提到的，針對三種空間屬性數據（pH值、有機質含量與全氮含量）中最符合正態分布，亦是三種屬性數據各三種（原始值、取對數與開平方）、共九種數據狀態中唯一一個通過Lilliefors正態分布檢驗的數值——全氮含量經過異常值剔除后的原始值，將其正態分布的圖像檢驗結果特展示如下。

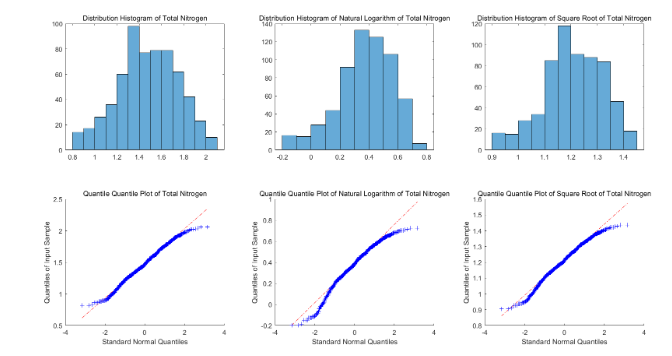
以上就是關于“Matlab計算變異函數并繪制經驗半方差圖的方法是什么”這篇文章的內容，相信大家都有了一定的了解，希望小編分享的內容對大家有幫助，若想了解更多相關的知識內容，請關注億速云行業資訊頻道。