您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹了Python八大排序怎么實現的相關知識,內容詳細易懂,操作簡單快捷,具有一定借鑒價值,相信大家閱讀完這篇Python八大排序怎么實現文章都會有所收獲,下面我們一起來看看吧。
基數排序的基本思想是先將數字按照個位數上數字的大小進行排序,排序之后再將已經排過序的數字再按照十位數上數字的大小進行排序,依次推類
# 統計這個列表中數字最大的數字有幾位 def radix_sort_nums(nums): max = nums[0] for i in nums: if max < i: max = i times = 0 while max > 0: max = int(max/10) times += 1 return times # 每個數字各個位置的數字大小,比如(123,1)則是3,(123,2)則是2 def get_num(num,n): return (int(num/(10**(n-1)))) % 10 # 主程序 def radix_sort(nums): count = 10*[None] # 定義的數組,用于存放當前位數的元素個數 bucket = len(nums)*[None] # 用于暫時存放排序結果 # 分別從個位/十位/百位開始循環 for pos in range(1, radix_sort_nums(nums)+1): # 每次排序完都要清空各個位數存放的數據統計 for i in range(10): count[i] = 0 for i in range(len(nums)): # 獲得0到9每個位數的個數 j = get_num(nums[i], pos) count[j] = count[j]+1 # 獲得相對應位數的邊界值 for i in range(1, 10): count[i] = count[i] + count[i-1] for i in range(len(nums)-1, -1, -1): # 求出相應位數的數字 j = get_num(nums[i], pos) #將元素按相應位數的上數字的大小排序 bucket[count[j]-1] = nums[i] #讓相應位數上數字相等的元素不會放在同一位置而被替代 count[j] = count[j]-1 # 將暫時存儲在bucket的元素數據返回到nums中 for i in range(0, len(nums)): nums[i] = bucket[i] return nums print(radix_sort([45, 32, 8, 33, 12, 22, 19, 97]))
歸并排序其實是將原數列分為很多個小數列將其排序,在小數列排序完之后,再將各個小數列進行排序,最后得到一個全部有序的數列

# 歸并排序 # 這個函數主要目的是為了實現合并并排序 def mergearray(nums, first, mid, last, temp): # i, j分別是第一個組數的第一個位置,第二組數的第一個位置 i, j, k = first, mid+1, 0 # 當倆邊數組都存在數的時候,依次比較對應位置的大小 while i <= mid and j <= last: if nums[i] <= nums[j]: temp[k] = nums[i] i = i+1 k = k+1 else: temp[k] = nums[j] j = j+1 k = k+1 # 第一組數還有多的數的情況 while i <= mid: temp[k] = nums[i] i = i+1 k = k+1 # 第二組數還有多的情況 while (j <= last): temp[k] = nums[j] j = j+1 k = k+1 # 將排列過的數組賦予nums(開始的時候只是部分有序,隨著遞歸最后變成全部有序) for i in range(k): nums[first+i] = temp[i] # 分組,利用遞歸 def merge_sort(nums,first,last,temp): if first < last: mid = int((first + last) / 2) # 分出第一組數 merge_sort(nums, first, mid, temp) # 分出第二組數 merge_sort(nums, mid+1, last, temp) # 合并并排序 mergearray(nums, first, mid, last, temp) def merge_sort_array(nums): # 創建一個和想要排序數列相同數量的空列表 temp = len(nums)*[None] # 利用遞歸進行排序 merge_sort(nums, 0, len(nums)-1, temp) print(merge_sort_array([45, 32, 8, 33, 12, 22, 19, 97]))
堆排序利用了二叉樹的結構,使子節點的值一直小于根節點
def big_endian(arr, start, end): root = start child = root * 2 + 1 # 左孩子 while child <= end: # 孩子比最后一個節點還大,也就意味著最后一個葉子節點了,就得跳出去一次循環,已經調整完畢 if child + 1 <= end and arr[child] < arr[child + 1]: # 為了始終讓其跟子元素的較大值比較,如果右邊大就左換右,左邊大的話就默認 child += 1 if arr[root] < arr[child]: # 父節點小于子節點直接交換位置,同時坐標也得換,這樣下次循環可以準確判斷:是否為最底層, # 是不是調整完畢 arr[root], arr[child] = arr[child], arr[root] root = child child = root * 2 + 1 else: break def heap_sort(nums): # 無序區大根堆排序 first = len(nums) // 2 - 1 for start in range(first, -1, -1): # 從下到上,從左到右對每個節點進行調整,循環得到非葉子節點 big_endian(nums, start, len(nums) - 1) # 去調整所有的節點 for end in range(len(nums) - 1, 0, -1): nums[0], nums[end] = nums[end], nums[0] # 頂部尾部互換位置 big_endian(nums, 0, end - 1) # 重新調整子節點的順序,從頂開始調整 return nums print(heap_sort([3, 1, 4, 9, 6, 7, 5, 8, 2, 10]))
簡單選擇排序的方法則是將所選值與剩下值中比他小的值進行比較
比如選取第一個值,往后找到比他小的值就與其對調,對調后的值再接下去進行比較,直至找到最小的值,隨后再第二個值……直至循環到倒數第二個值.
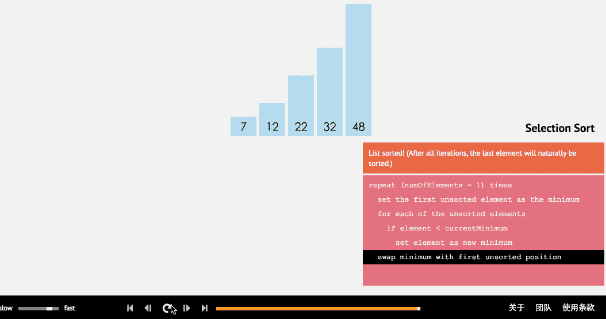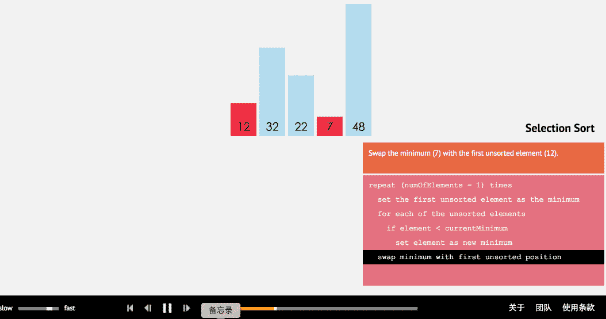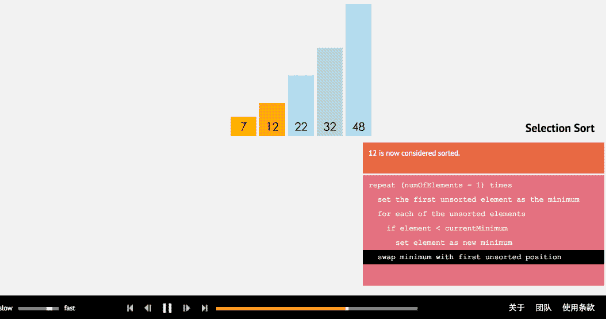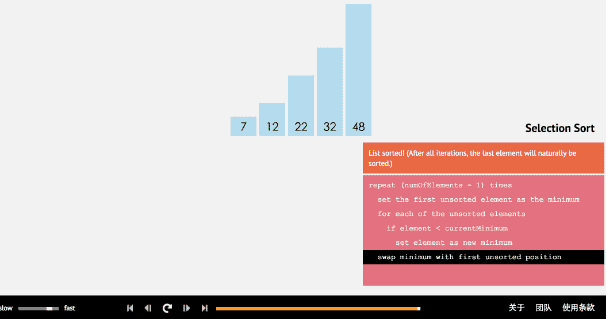
def select_sort(nums): # 遍歷所有的值 for i in range(len(nums)): # 當前位置初始值 min = nums[i] # 與比他后面的值進行比較,小則互換 for j in range(i+1, len(nums)): if nums[j] < min: nums[j], min = min, nums[j] # 將值返回數列 nums[i] = min return nums print(select_sort([45, 32, 8, 33, 12, 22, 19, 97]))
首先遍歷所有元素,隨后從第一個數開始將數列從后往前遍歷,如果后面的數小于前面的數,則互換位置,依次推類,直到遍歷完成
# 直接插入排序 def insert_sort(nums): for i in range(len(nums)-1): for j in range(i, -1, -1): if nums[j] > nums[j+1]: nums[j], nums[j + 1] = nums[j + 1], nums[j] return nums print(insert_sort([45, 32, 8, 33, 12, 22, 19, 97]))
希爾排序其實就相當于對直接插入排序的升級版,每次都選取一半的長度,隨后利用直接插入法進行排序,從而更快的獲得結果
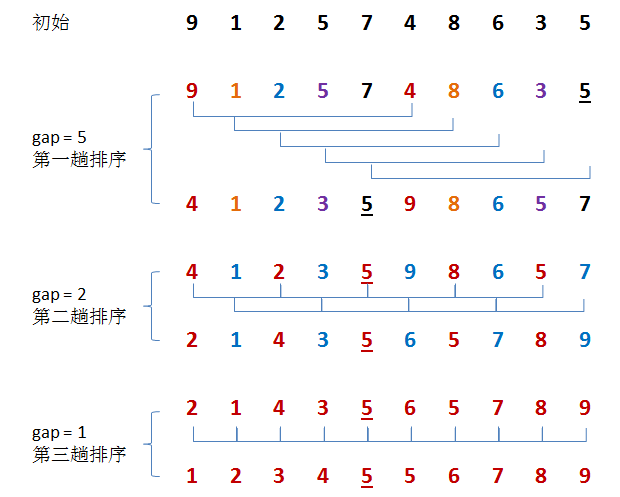
def insert_shell(nums): # 初始化l值,此處利用序列長度的一半為其賦值 l = int(len(nums)/2) # 第一層循環:依次改變l值對列表進行分組 while l >= 1: # 下面:利用直接插入排序的思想對分組數據進行排序 for i in range(len(nums) - 1): for j in range(i, -1, -1): if nums[j] > nums[j + 1]: nums[j], nums[j + 1] = nums[j + 1], nums[j] # while循環條件折半 l = int(l/2) return nums
快速排序首先得選取一個基準值,這個代碼用第一個數作為基準值,將比基準值小的值放到左邊,比基準值大的值放到右邊,隨后再將左邊后右邊按照上述方法進行排序,直到完全正確為止
# 實現快速排序方法的函數 def quick_sort_num(nums,start,end): if start < end: # 定義基準值為第一個數 i, j, pivot = start, end, nums[start] while i < j: # 將基準數右邊的數中比基準數小的放到左邊 while i < j and nums[j] >= pivot: j = j-1 if i < j: nums[i] = nums[j] i = i+1 # 將基準數左邊的數中比基準數大的數放到右邊 while i < j and nums[i] < pivot: i = i+1 if i < j: nums[j] = nums[i] j = j-1 nums[i] = pivot # 分別將基準數左邊的數列和右邊的數列進行遞歸 quick_sort_num(nums, start, i-1) quick_sort_num(nums, i+1, end) return nums # 快速排序主體函數 def quick_sort(nums): start = 0 end = len(nums)-1 nums = quick_sort_num(nums, start, end) return nums print(quick_sort([45, 32, 8, 33, 12, 22, 19, 97]))
冒泡排序是最簡單的排序,依次將左右倆個元素進行比較,每次比較完最后的一個數必定是最大的,依次推類,直到全部元素都比較玩
def bubble_sort(nums): # 交換的輪數 for i in range(len(nums) - 1): # 每一輪交換 for j in range(len(nums) - i - 1): # 比較值,并根據大小進行互換 if nums[j] > nums[j + 1]: nums[j], nums[j + 1] = nums[j + 1], nums[j] return nums print(bubble_sort([45, 32, 8, 33, 12, 22, 19, 97]))
我們先創建一個列表,列表中有10000條數據,隨后用相同的數據進行測試
import random lis = [] for i in range(10000): i = random.randint(0,500) lis.append(i) print(lis)
創出來的數據就不進行展示了。。
隨后我們進行測試:
冒泡排序法:11.535502672195435 直接插入排序法:12.057243585586548 希爾排序法:86.3020749092102(大概是我的方法不大好吧,我差點以為他排不出來了) 基數排序法:0.051932334899902344(老大哥就是牛皮) 歸并排序法:0.08577108383178711(233) 快速排序:0.04795527458190918 堆排序:0.09175491333007812
根據自己的測試,基數排序,歸并排序,快速排序,和堆排序速度很快,感覺隨著代碼量的增長時間增長很慢,其余的幾個則不盡如人意了。
關于“Python八大排序怎么實現”這篇文章的內容就介紹到這里,感謝各位的閱讀!相信大家對“Python八大排序怎么實現”知識都有一定的了解,大家如果還想學習更多知識,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。