Python如何實現蒙特卡洛模擬

這篇“Python如何實現蒙特卡洛模擬”文章的知識點大部分人都不太理解，所以小編給大家總結了以下內容，內容詳細，步驟清晰，具有一定的借鑒價值，希望大家閱讀完這篇文章能有所收獲，下面我們一起來看看這篇“Python如何實現蒙特卡洛模擬”文章吧。

什么是蒙特卡洛模擬

蒙特卡洛模擬是一種基于概率統計的方法，通過隨機模擬來計算出某個事件發生的概率。在項目管理中，蒙特卡洛模擬主要用于計算項目工期、成本等關鍵指標的概率分布，幫助項目經理更好地進行風險管理和決策。

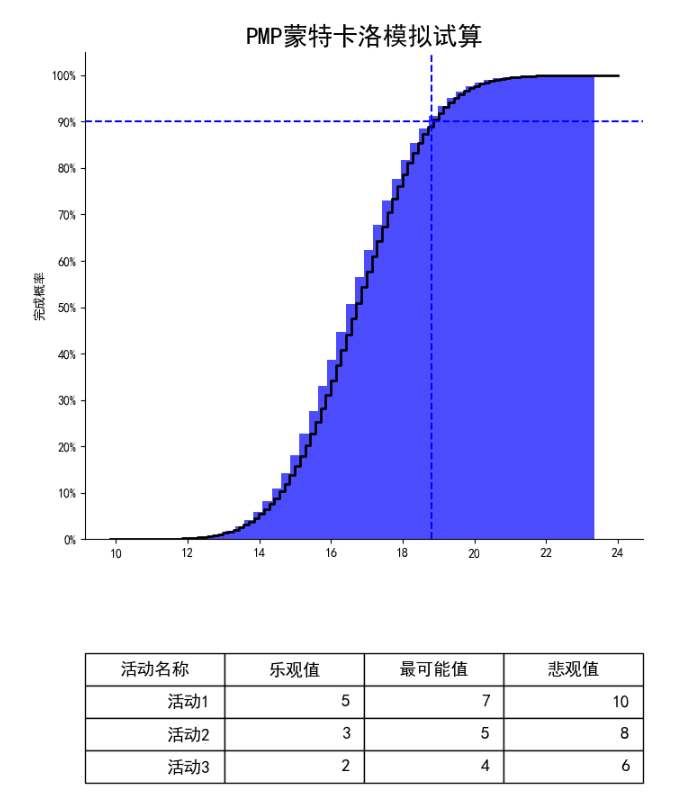
讓我們來看上面這張圖， 這張圖是針對三個項目活動:活動1、活動2、活動3進行的蒙特卡洛模擬。 模擬的依據是這三個活動的三點估算結果。 然后讓計算機進行了1,000,000次隨機預算， 得出的上面這張圖。

我們拿上邊這張圖的藍色虛線的交叉舉例，這個點指的是什么呢？ 我們看Y軸，這里的90%指的是完工概率90%。 這個點對應的橫軸將近19天的樣子。也就是說，通過計算機100萬次的模擬。在19天以下完成項目的概率是90%。

做過項目的同學都知道， 客戶或者領導總是希望我們快些快些再快些。 領導說，19天沒有，只有16天。 這時候，作為項目經理通過上面的圖，發現，X軸16天對應Y軸的值大概在30%左右。 你就問領導：成功率只有30%喲， 你賭還是不賭~

這不失為一種不錯的“科學算命”的方式。 關鍵是簡單，還有概率論給你撐腰。

Python實現

在Python中如何計算項目管理的蒙特卡洛模擬呢？其實很簡單，我們可以使用Python中的numpy和matplotlib庫來進行計算和繪圖。下面田老師給出完整的代碼：

#!/usr/bin/env python
# -*- coding:utf-8 -*-
"""
#-----------------------------------------------------------------------------
#                     --- TDOUYA STUDIOS ---
#-----------------------------------------------------------------------------
#
# @Project : di08-tdd-cdg-python-learning
# @File    : monte_carlo.py
# @Author  : tianxin.xp@gmail.com
# @Date    : 2023/3/12 18:22
#
# 用Python實現蒙特卡洛模擬
#
#--------------------------------------------------------------------------"""
from datetime import datetime

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.ticker import FuncFormatter, MultipleLocator
from scipy.stats import norm

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


def to_percent(y, position):
    # 將縱軸用百分數表示
    return '{:.0f}%'.format(100 * y)


class Activity:
    """ 活動類，用于表示一個項目中的活動

   Attributes:
       name (str): 活動名稱
       optimistic (float): 樂觀時間
       pessimistic (float): 悲觀時間
       most_likely (float): 最可能時間
   """

    def __init__(self, name, optimistic, pessimistic, most_likely):
        """
            初始化活動類

            Args:
                name (str): 活動名稱
                optimistic (float): 樂觀時間
                pessimistic (float): 悲觀時間
                most_likely (float): 最可能時間
        """
        self.name = name
        self.optimistic = optimistic
        self.pessimistic = pessimistic
        self.most_likely = most_likely


class PMP:
    """
    PMP類用于進行項目管理中的相關計算：
    方法：
    monte_carlo_simulation : 蒙特卡洛模擬試算，包括計算項目工期、平均值、標準差、繪制積累圖和概率密度曲線等功能。
    """

    def __init__(self, activities):
        """
        初始化PMP類，傳入活動列表。
        :param activities: 活動列表，包括活動名稱、樂觀值、最可能值和悲觀值。
        """
        self.activities = activities

    def monte_carlo_simulation(self, n):
        """
        進行蒙特卡洛模擬試算，計算項目工期、平均值、標準差、繪制積累圖和概率密度曲線等。
        :param n: 模擬次數。
        """
        # 模擬參數和變量
        t = []
        for activity in self.activities:
            t.append(np.random.triangular(activity.optimistic, activity.most_likely, activity.pessimistic, n))

        # 計算項目工期
        project_duration = sum(t)

        # 計算平均值和標準差
        mean_duration = np.mean(project_duration)
        std_duration = np.std(project_duration)

        # 繪制積累圖
        fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(8, 10), gridspec_kw={'height_ratios': [3, 1]})

        ax1.hist(project_duration, bins=50, density=True, alpha=0.7, color='blue', cumulative=True)
        ax1.yaxis.set_major_locator(MultipleLocator(0.1))
        ax1.yaxis.set_major_formatter(FuncFormatter(to_percent))
        ax1.set_ylabel('完成概率')
        ax1.set_title('PMP蒙特卡洛模擬試算', fontsize=20)

        # 繪制概率密度曲線
        xmin, xmax = ax1.get_xlim()
        x = np.linspace(xmin, xmax, 100)
        p = norm.cdf(x, mean_duration, std_duration)
        ax1.plot(x, p, 'k', linewidth=2, drawstyle='steps-post')

        # 找到完成概率90%的點
        x_90 = norm.ppf(0.9, mean_duration, std_duration)

        # 繪制垂線
        ax1.axvline(x_90, linestyle='--', color='blue')
        ax1.axhline(0.9, linestyle='--', color='blue')

        # 隱藏右邊和上方的坐標軸線
        ax1.spines['right'].set_visible(False)
        ax1.spines['top'].set_visible(False)

        # 添加表格
        col_labels = ['活動名稱', '樂觀值', '最可能值', '悲觀值']

        cell_text = [[activity.name, activity.optimistic, activity.most_likely, activity.pessimistic] for activity in
                     self.activities]
        table = ax2.table(cellText=cell_text, colLabels=col_labels, loc='center')

        # 設置表格的字體大小和行高
        table.auto_set_font_size(False)
        table.set_fontsize(14)

        # # 設置表格的行高為1.5倍原來的高度
        for i in range(len(self.activities) + 1):
            table._cells[(i, 0)].set_height(0.2)
            table._cells[(i, 1)].set_height(0.2)
            table._cells[(i, 2)].set_height(0.2)
            table._cells[(i, 3)].set_height(0.2)

        ax2.axis('off')

        # 調整子圖之間的間距和邊距
        plt.subplots_adjust(hspace=0.3, bottom=0.05)

        # 保存圖表
        now = datetime.now().strftime('%Y%m%d%H%M%S')
        plt.savefig('monte_carlo_simulation_{}.png'.format(now))

        # 顯示圖形
        plt.show()


if __name__ == '__main__':
    # 模擬參數和變量
    n = 1000000  # 模擬次數

    # 活動的工期分布
    activities = [
        Activity('活動1', 5, 10, 7),
        Activity('活動2', 3, 8, 5),
        Activity('活動3', 2, 6, 4)
    ]

    # 進行蒙特卡洛模擬
    pmp = PMP(activities)
    pmp.monte_carlo_simulation(n)

以上就是關于“Python如何實現蒙特卡洛模擬”這篇文章的內容，相信大家都有了一定的了解，希望小編分享的內容對大家有幫助，若想了解更多相關的知識內容，請關注億速云行業資訊頻道。