您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“C++最短路徑Dijkstra算法如何實現”,在日常操作中,相信很多人在C++最短路徑Dijkstra算法如何實現問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”C++最短路徑Dijkstra算法如何實現”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
一般來說,有關圖的算法的存儲結構為鄰接表、鄰接矩陣,這次就以鄰接矩陣存儲為例,求出下圖的最短路徑:
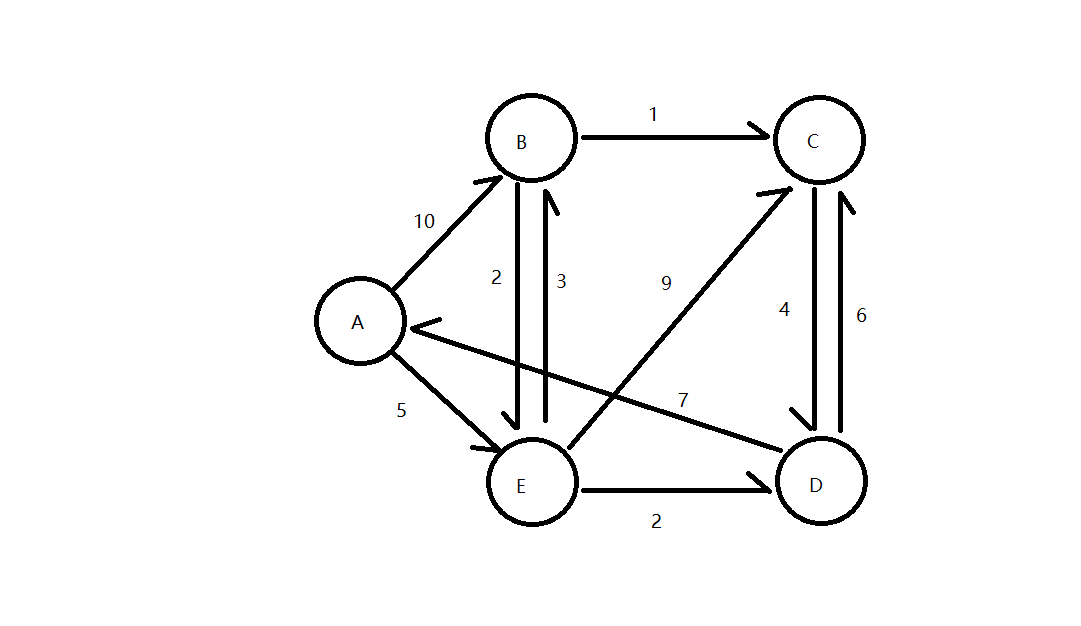
需要有三個數組:
final[]:布爾型,用來記錄頂點是否已找到最短路徑
dist[]:整形,記錄最短路徑長度(帶權)
path[]:整形,記錄當前頂點的前驅結點下標
#define MAXVERTEX 6 bool final[MAXVERTEX]; int dist[MAXVERTEX]; int path[MAXVERTEX];
對于起始頂點需要將final 設為true,dist 設為 0,path 設為-1
遍歷所有與起始頂點相連的結點,找到一個權值最小的邊,并將對應頂點 i 加入到最短路徑,即 final[i] = true,之后再遍歷與 i 相鄰的頂點,若final 值為false 且dist 值小于dist[i]+dist[i][] 就將其dist 值更新,path 值改為 i。
第一輪結束后會有兩個頂點的 final 值為 true,實際上最大的循環只需要進行n - 1次,從第一輪結束后我們從值為 false 的頂點中找 dist 值最小的頂點,將其fianl 值設為 true,檢查與其相鄰頂點的path 值和dist 值可否更新(判斷與dist[i]+dist[i][]的大小),重復第二輪的操作直至大循環結束。這樣最終的 dist 存放的就是起始頂點到對應下標頂點的最短路徑長度,而path 存放的就是最短路徑。
#include<iostream>
using namespace std;
// 模擬實現Dijkstra算法,不適用于存在負值的帶權圖
#define MAXVERTEX 6
typedef struct {
char Vertex[MAXVERTEX]; //頂點集
int Edge[MAXVERTEX][MAXVERTEX]; // 存放權值
int vernum, arcnum; // 頂點數和邊數
}MGraph;
// 初始化圖
void InitGraph(MGraph& G) {
G.Vertex[0] = 'A';
G.Vertex[1] = 'B';
G.Vertex[2] = 'C';
G.Vertex[3] = 'D';
G.Vertex[4] = 'E';
G.vernum = 5;
G.arcnum = 10;
// 圖中邊權值均設為無窮大
for (int i = 0; i < G.vernum; i++) {
for (int j = 0; j < G.vernum; j++) {
G.Edge[i][j] = INT_MAX;
}
}
// 根據具體圖形設置具體權值
G.Edge[0][1] = 10; // 諸如此類
G.Edge[0][4] = 5;
G.Edge[1][2] = 1;
G.Edge[1][4] = 2;
G.Edge[4][1] = 3;
G.Edge[2][3] = 4;
G.Edge[3][2] = 6;
G.Edge[4][3] = 2;
G.Edge[3][0] = 7;
G.Edge[4][2] = 9;
}
bool final[MAXVERTEX];
int dist[MAXVERTEX];
int path[MAXVERTEX];
void Dijkstra(MGraph G,int v) {
for (int i = 0; i < G.vernum; i++) {
final[i] = false;
dist[i] = G.Edge[v][i];
path[i] = (G.Edge[v][i] == INT_MAX ? -1 : v);
}
final[v] = true;
dist[v] = 0;
// 第一輪
int index =v; // 權值最小的邊頂點下標
int para = INT_MAX;
for (int j = 0; j < G.vernum; j++) {
if (final[j] == false && G.Edge[v][j] < para) {
para = G.Edge[v][j];
index = j;
}
}
// 第二輪及以后
for (int i = 0; i < G.vernum; i++) {
for (int c = 0; c < G.vernum; c++) {
if (final[c] ==false && G.Edge[index][c] < INT_MAX) {
if (G.Edge[index][c] + dist[index] < dist[c]) {
dist[c] = G.Edge[index][c] + dist[index];
path[c] = index;
}
}
}
// 找到final 為false的頂點中權值最小的頂點下標
int temp = INT_MAX;
int in = v;
for (int i = 0; i < G.vernum; i++) {
if (final[i] == false && dist[i] < temp) {
temp = dist[i];
in = i;
}
}
index = in; // 更新下標
final[index] = true;
}
}
void print_path(MGraph G ,int v) {
cout << "對應的最短路徑為:";
cout << G.Vertex[v] << "->";
for (int i = 0; i < G.vernum; i++) {
if (path[v] != 1) {
cout << G.Vertex[path[v]] << "->";
v = path[v];
}
}
cout << G.Vertex[1] << endl;
}
int main() {
MGraph G;
InitGraph(G);
Dijkstra(G, 1);
cout << "頂點B到頂點D的最小花費為:"<< dist[3] << endl;
print_path(G, 3);
}運行結果:
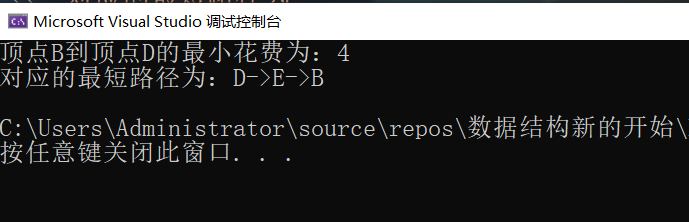
想得到哪個頂點的最短路徑就在主函數中 Dijkstra(G, ?) 第二個參數寫入下標即可,其他對應關系:頂點下標 0~4 對應 A~E,所以在 cout那行代碼中dist下標要與到達頂點一致,而出發頂點要與自己填入的下標一致。
print_path 函數里的 if 語句中的下標也要和起始頂點下標一致,最后的一個cout也同樣處理
例如:
Dijkstra(G,0);
// dist[2];
cout<<"頂點A到頂點C的最短路徑為"<<dist[2]<<endl;
void print_path(MGraph G ,int v) {
cout << "對應的最短路徑為:";
cout << G.Vertex[v] << "->";
for (int i = 0; i < G.vernum; i++) {
if (path[v] != 0) {
cout << G.Vertex[path[v]] << "->";
v = path[v];
}
}
cout << G.Vertex[0] << endl;
}
Dijkstra 算法的時間復雜度只與頂點有關,可以通過算法分析看出來每次都要對一個頂點遍歷尋找與其相鄰頂點的最小權值,所以時間復雜度應為:O(n2),也可以寫成O(∣V∣2),V 是頂點的含義(vertex)。
到此,關于“C++最短路徑Dijkstra算法如何實現”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。