您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“Python如何實現曲線的肘部點檢測”,在日常操作中,相信很多人在Python如何實現曲線的肘部點檢測問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”Python如何實現曲線的肘部點檢測”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
**肘形曲線(elbow curve)**類似人胳膊狀的曲線,拐點在肘部。**膝形曲線(knee curve)人腿形的曲線,拐點在膝蓋。這類曲線和二八原則(即帕托累法則)**不謀而合,做決策時,自然選擇肘點或膝點做參考。按照拐點在左還是右側來分,細分為:左膝點曲線,右膝點曲線,左肘點曲線,右肘點曲線。
曲線示意圖如下:
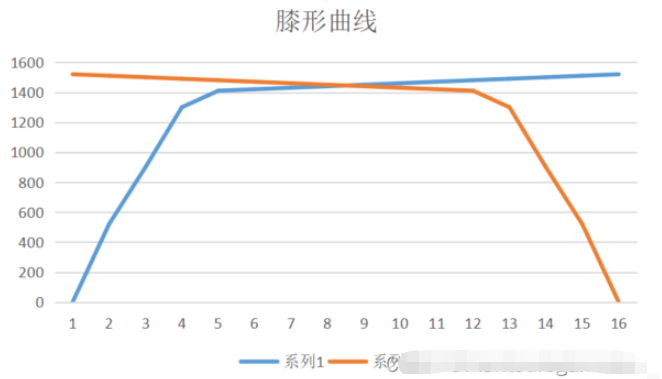
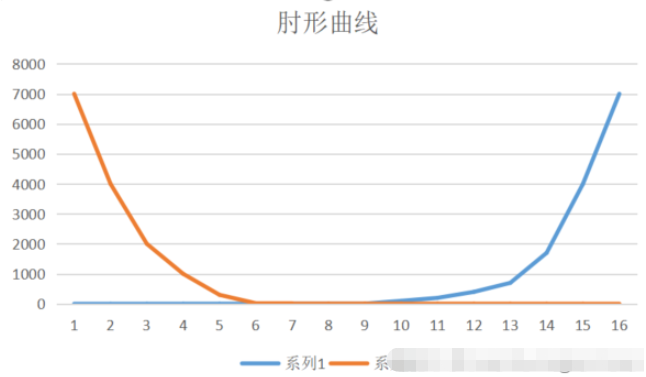
左膝點曲線膝點在左邊的曲線(術語是我自己起的,明白意思就好,膝點在左邊)如下:
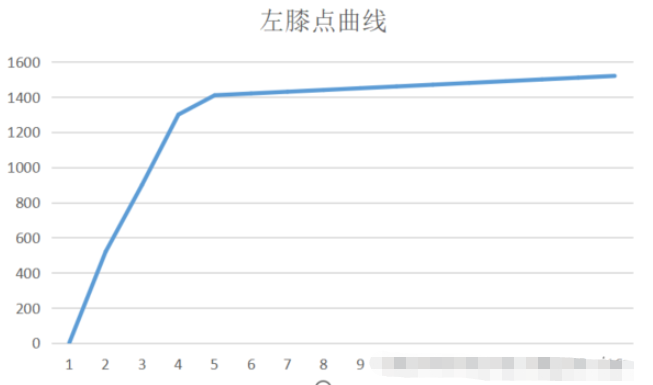
從形狀上,四種曲線沒有大的區別,可以相互轉化:
肘曲線與膝曲線相互轉化,用曲線最大值減去曲線各點值即可。同類型曲線,左右拐點轉化,就是切換升序降序排序即可。
它們都可以計算拐點,其中以左膝點曲線(見下圖)計算拐點最簡單,所以以其為標準曲線。
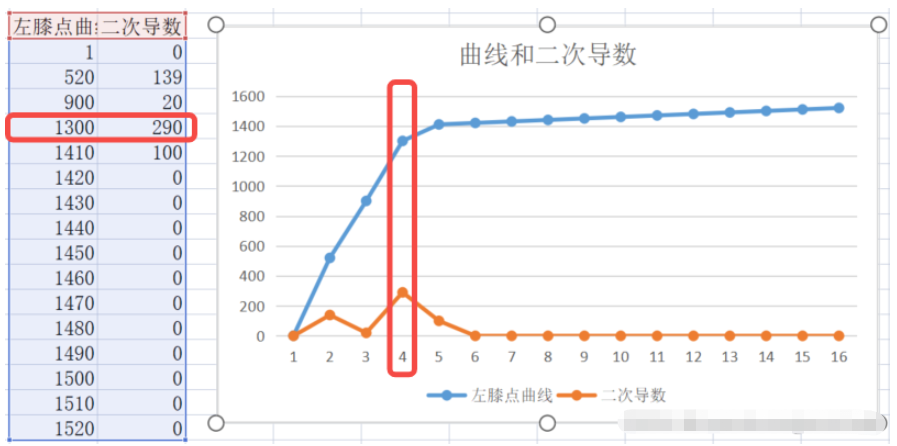
左膝點曲線,原理是其二次曲線導數最大點,如下:
對于離散序列來說,當x軸差為1時,二次曲線計算公式為:
f′′(xi)=f(xi−1)+f(xi+1)−2*f(xi)
支持:Python 3.7, 3.8, 3.9, and 3.10. 安裝如下:
$ conda install -c conda-forge kneed # 或者 $ pip install kneed # To install only knee-detection algorithm $ pip install kneed[plot] # To also install plotting functions for quick
使用如下:
from kneed import DataGenerator, KneeLocator x, y = DataGenerator.figure2() print([round(i, 3) for i in x]) print([round(i, 3) for i in y]) # out: [0.0, 0.111, 0.222, 0.333, 0.444, 0.556, 0.667, 0.778, 0.889, 1.0] # out: [-5.0, 0.263, 1.897, 2.692, 3.163, 3.475, 3.696, 3.861, 3.989, 4.091] kneedle = KneeLocator(x, y, S=1.0, curve="concave", direction="increasing") print(round(kneedle.knee, 3)) # out: 0.222 print(round(kneedle.elbow, 3)) # out: 0.222
到此,關于“Python如何實現曲線的肘部點檢測”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。