您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“怎么用pytorch中backward()方法自動求梯度”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!
x = torch.arange(-8.0, 8.0, 0.1, requires_grad= True) y = x.relu()
x為源張量,基于源張量x得到的張量y為結果張量。
一個標量調用它的backward()方法后,會根據鏈式法則自動計算出源張量的梯度值。
2.1、結果張量是一維張量
基于以上例子,就是將一維張量y變成標量后,然后通過調用backward()方法,就能自動計算出x的梯度值。
那么,如何將一維張量y變成標量呢?
一般通過對一維張量y進行求和來實現,即y.sum()。
一個一維張量就是一個向量,對一維張量求和等同于這個向量點乘一個等維的單位向量,使用求和得到的標量y.sum()對源張量x求導與y的每個元素對x的每個元素求導結果是一樣的,最終對源張量x的梯度求解沒有影響。
因此,代碼如下:
y.sum().backward() x.grad
2.2、結果張量是二維張量或更高維張量
撇開上面例子,結果變量y可能是二維張量或者更高維的張量,這時可以理解為一般點乘一個等維的單位張量(點乘,是向量中的概念,這樣描述只是方便理解)
代碼如下:
y.backward(torch.ones_like(y))#grad_tensors=torch.ones_like(y) x.grad
在一元函數中,某點的梯度標的就說某點的導數. 在多元函數中某點的梯度表示的是由每個自變量所對應的偏導數所組成的向量
在前面的線性回歸中 就像y = wx + b方程中求出w參數最優的解,就需要對w參數進行偏導數的求取,然后通過偏導數的值來調整w參數以便找到最優解。
在PyTorch中可以使用torch.autograd.backward()方法來自動計算梯度
在定義張量時,可以指定requires_grad=True表示這個張量可以求偏導數
import torch # 隨機出張量x 指定可以計算偏導數 x = torch.randn(1,requires_grad=True) # y和z張量不可以求偏導 y = torch.randn(1) z = torch.randn(1) # f1中有張量允許求偏導 f1 = 2*x + y # f2中沒有張量可以允許求偏導 f2 = y + z # 打印兩個方程的梯度 print(f1.grad_fn) print(f2.grad_fn)
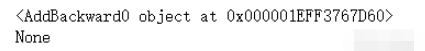
得出結論:
f1中有允許可以求偏導的張量存在才可以求梯度
grad_fn為梯度
1. 求x的偏導數
# 可以求梯度的變量先使用backward()反向傳播 f1.backward() # 使用張量的grad屬性拿到偏導數的值 x.grad

2. 停止梯度的計算
張量.requires_grad_(False)
# 創建張量 指定可以求偏導 a = torch.randn(2,2,requires_grad=True) # a對應的b變量 b = ((a * 3)/(a - 1)) # 查看梯度 print(b.grad_fn) # 停止a張量可以求偏導 a.requires_grad_(False) # 再次指定b對應變量 b = ((a * 3) / (a - 1)) # 為None了 print(b.grad_fn)
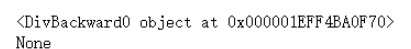
3. 獲取到可以求偏導數的張量相同的內容,但是新變量不可以求偏導
張量.detach()方法
a = torch.randn(2,2,requires_grad=True) # 可以求偏導的張量返回一個相同的張量但是不可以求偏導數 b = a.detach() print(a.requires_grad) print(b.requires_grad)
4. 在作用域中張量不可計算偏導數
with torch.no_grad(): 內的整個作用域
a = torch.randn(2, 2, requires_grad=True) print((a ** 2).requires_grad) with torch.no_grad(): print((a ** 2).requires_grad)
在PyTorch中,如果我們利用torch.autograd.backward()方法求解張量的梯度, 在多次運行該函數的情況下, 該函數會將計算得到的梯度累加起來。
所以在函數中計算張量的偏導數,每次計算完修改完參數要清空梯度的計算。
不清空梯度計算:
x = torch.ones(4, requires_grad=True)
y = (2*x + 1).sum()
z = (2*x).sum()
y.backward()
print("第一次偏導:",x.grad)
z.backward()
print("第二次偏導:",x.grad)會累加

使用張量.grad.zero_()方法清空梯度的計算:
x = torch.ones(4, requires_grad=True)
y = (2*x + 1).sum()
z = (2*x).sum()
y.backward()
x.grad.zero_()
print("第一次偏導:",x.grad)
z.backward()
print("第二次偏導:",x.grad)
“怎么用pytorch中backward()方法自動求梯度”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。