您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇“Java中二分法怎么實現”文章的知識點大部分人都不太理解,所以小編給大家總結了以下內容,內容詳細,步驟清晰,具有一定的借鑒價值,希望大家閱讀完這篇文章能有所收獲,下面我們一起來看看這篇“Java中二分法怎么實現”文章吧。

思路:
由于是有序數組,可以先得到中點位置,中點可以把數組分為左右半邊。
如果中點位置的值等于目標值,直接返回中點位置。
如果中點位置的值小于目標值,則去數組中點左側按同樣的方式尋找。
如果中點位置的值大于目標值,則取數組中點右側按同樣的方式尋找。
如果最后沒有找到,則返回:-1。
代碼
class Solution {
public int search(int[] arr, int t) {
if (arr == null || arr.length < 1) {
return -1;
}
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l) >> 1);
if (arr[m] == t) {
return m;
} else if (arr[m] > t) {
r = m - 1;
} else {
l = m + 1;
}
}
return -1;
}
}時間復雜度 O(logN)。
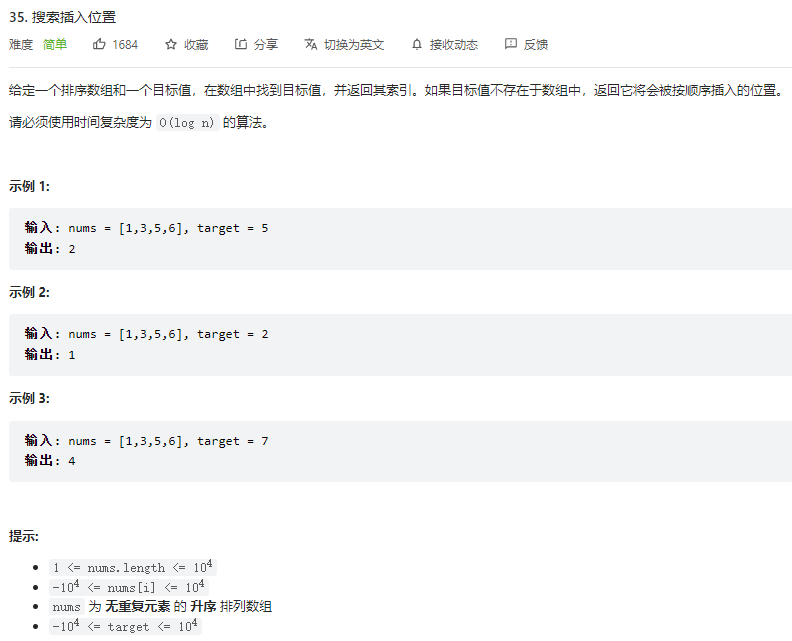
示例 1:
輸入: nums = [1,3,5,6], target = 5
輸出: 2
說明:如果要在num這個數組中插入 5 這個元素,應該是插入在元素 3 和 元素 5 之間的位置,即 2 號位置。
示例 2:
輸入: nums = [1,3,5,6], target = 2
輸出: 1
說明:如果要在num這個數組中插入 2 這個元素,應該是插入在元素 1 和 元素 3 之間的位置,即 1 號位置。
示例 3:
輸入: nums = [1,3,5,6], target = 7
輸出: 4
說明:如果要在num這個數組中插入 7 這個元素,應該是插入在數組末尾,即 4 號位置。
通過上述示例可以知道,這題本質上就是求在一個有序數組中,找大于等于某個數最左側的位置,如果不存在,就返回數組長度(表示插入在最末尾位置)
我們只需要在上例基礎上進行簡單改動即可,上例中,我們找到滿足條件的位置就直接return了
if (arr[m] == t) {
return m;
}在本問題中,因為要找到最左側的位置,所以,在遇到相等的時候,只需要先把位置記錄下來,不用直接返回,然后繼續去左側找是否還有滿足條件的更左邊的位置。
同時,在遇到arr[m] > t條件下,也需要記錄下此時的m位置,因為這也可能是滿足條件的位置。
代碼:
class Solution {
public static int searchInsert(int[] arr, int t) {
int ans = arr.length;
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l)>>1);
if (arr[m] >= t) {
ans = m;
r = m - 1;
} else {
l = m + 1;
}
}
return ans;
}
}整個算法的時間復雜度是O(logN)。
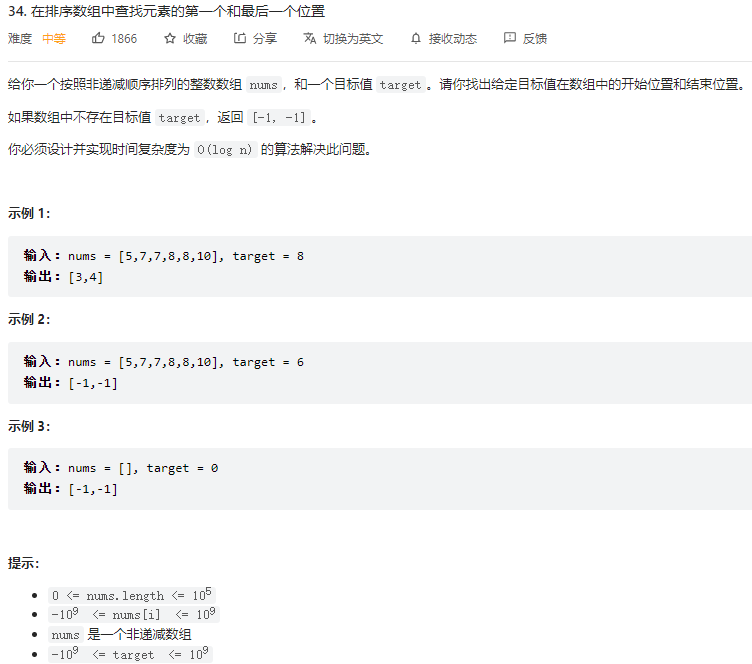
思路
本題也是用二分來解,當通過二分找到某個元素的時候,不急著返回,而是繼續往左(右)找,看能否找到更左(右)位置匹配的值。
代碼如下:
class Solution {
public static int[] searchRange(int[] arr, int t) {
if (arr == null || arr.length < 1) {
return new int[]{-1, -1};
}
return new int[]{left(arr,t),right(arr,t)};
}
public static int left(int[] arr, int t) {
if (arr == null || arr.length < 1) {
return -1;
}
int ans = -1;
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l) >> 1);
if (arr[m] == t) {
ans = m;
r = m - 1;
} else if (arr[m] < t) {
l = m +1;
} else {
// arr[m] > t
r = m - 1;
}
}
return ans;
}
public static int right(int[] arr, int t) {
if (arr == null || arr.length < 1) {
return -1;
}
int ans = -1;
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l) >> 1);
if (arr[m] == t) {
ans = m;
l = m + 1;
} else if (arr[m] < t) {
l = m +1;
} else {
// arr[m] > t
r = m - 1;
}
}
return ans;
}
}時間復雜度 O(logN)。
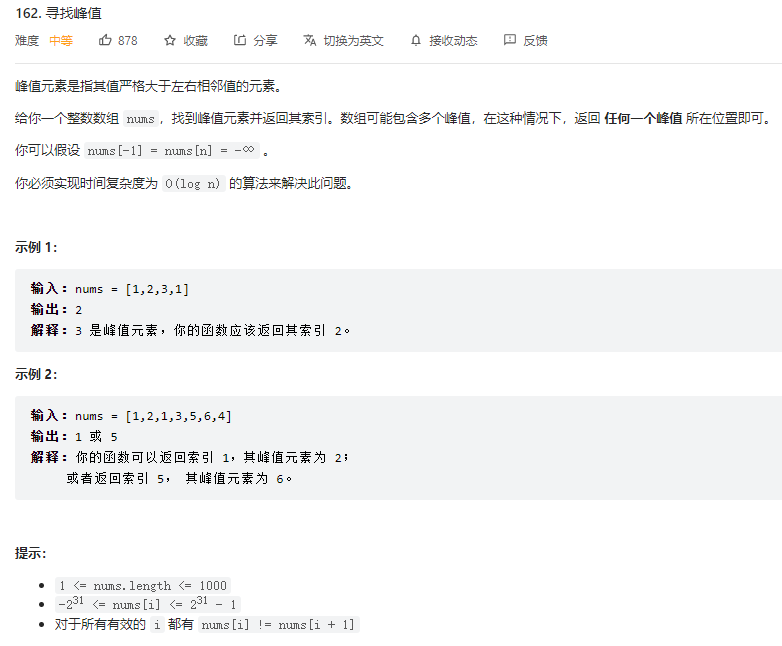
思路
假設數組長度為N,首先判斷0號位置的數和N-1位置的數是不是峰值位置。
0號位置只需要和1號位置比較,如果0號位置大,0號位置就是峰值位置,可以直接返回。
N-1號位置只需要和N-2號位置比較,如果N-1號位置大,N-1號位置就是峰值位置,可以直接返回。
如果0號位置和N-1在上輪比較中均是最小值,那么數組的樣子必然是如下情況:

由上圖可知,[0..1]區間內是增長趨勢, [N-2...N-1]區間內是下降趨勢。
那么峰值位置必在[1...N-2]之間出現。
此時可以通過二分來找峰值位置,先來到中點位置,假設為mid,如果中點位置的值比左右兩邊的值都大:
arr[mid] > arr[mid+1] && arr[mid] > arr[mid-1]
則mid位置即峰值位置,直接返回。
否則,有如下兩種情況:
情況一:mid 位置的值比 mid - 1 位置的值小
趨勢如下圖:

則在[1...(mid-1)]區間內繼續二分。
情況二:mid 位置的值比 mid + 1 位置的值小
趨勢是:

則在[(mid+1)...(N-2)]區間內繼續上述二分。
完整代碼
public class LeetCode_0162_FindPeakElement {
public static int findPeakElement(int[] nums) {
if (nums.length == 1) {
return 0;
}
int l = 0;
int r = nums.length - 1;
if (nums[l] > nums[l + 1]) {
return l;
}
if (nums[r] > nums[r - 1]) {
return r;
}
l = l + 1;
r = r - 1;
while (l <= r) {
int mid = l + ((r - l) >> 1);
if (nums[mid] > nums[mid + 1] && nums[mid] > nums[mid - 1]) {
return mid;
}
if (nums[mid] < nums[mid + 1]) {
l = mid + 1;
} else if (nums[mid] < nums[mid - 1]) {
r = mid - 1;
}
}
return -1;
}
}時間復雜度O(logN)。
以上就是關于“Java中二分法怎么實現”這篇文章的內容,相信大家都有了一定的了解,希望小編分享的內容對大家有幫助,若想了解更多相關的知識內容,請關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。