您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要講解了“怎么使用Flutter繪制分數邊形及多邊形漸變動畫”,文中的講解內容簡單清晰,易于學習與理解,下面請大家跟著小編的思路慢慢深入,一起來研究和學習“怎么使用Flutter繪制分數邊形及多邊形漸變動畫”吧!
在定義繪制分數邊形的繪制方法之前,我們先來看整數邊形是如何繪制的:
繪制正三角形,我們會在圓上找出三等分點,然后依次連接這三個點,這就是正三角形的繪制方法。
而且繪制的時候我們通常會固定一個起點,然后從這個起點開始等分。
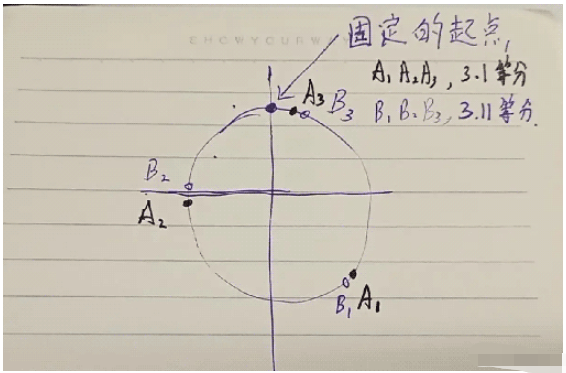
分數邊形的繪制也是一樣的道理,比如3.1邊形的繪制,我們需要找到四個點
我們先固定一個起點,然后從這個起點開始旋轉(2*pi/3.1)個弧度,這樣依次找到剩下三個點,(因為不是等分,所以可這樣找下去可以找到無數個點,但我們只需要找四個點),而且當我們給到兩個很相近的分數,比如3.1和3.11時,3.1邊形對應的四個點和3.11對應的四個點,由于它們的起點是固定的,剩下各自的三個點對應的位置都是很接近的(因為3.1和3.11對應的弧度是很接近的),這樣一直畫到4.0邊形,就完成了從三邊形到四邊形的漸變動畫。
獲取多邊形頂點
List<Offset> points = [];
List<Offset> getPolygonPoints1(double sides) {
for (int i = 0; i < sides.ceil(); i++) {
double x, y;
x = radius * sin(i * 2 * pi / sides);
y = -radius * cos(i * 2 * pi / sides);
points.add(Offset(x, y));
}
return points;
}獲取到多邊形頂點之后我們就可以在Custompaint的paint函數中將其繪制出來:
@override
void paint(Canvas canvas, Size size) {
Paint paint = Paint()
..color = const Color(0xFF47484B)
..style = PaintingStyle.stroke
..strokeWidth = 1
..isAntiAlias = true;
List<Offset> points = getPolygonPoints1(progress);
for (int i = 0; i < points.length; i++) {
canvas.drawLine(
points[i % points.length], points[(i + 1) % points.length], paint);
}
}但是如果我想要下圖這種效果,當邊數為奇數時,頂點位于最上方,邊數由奇數變成偶數時,最上方的頂點分裂成兩個
想要達到這種效果,我們只需要將代碼改進一下,不再固定起始點,而是在邊數由奇數變為偶數時,將起始點的弧度由(pi / sides)漸變為0,由偶數變位奇數時,起始點弧度由0變為(pi / sides)。
代碼如下:
List<Offset> getPolygonPoints2(double sides) {
for (int i = 0; i < sides.ceil(); i++) {
double x, y;
if (sides.ceil() % 2 == 0) {
x = radius *
sin(lerpDouble(0, (pi / sides), sides - sides.floor())! +
i * 2 * pi / sides);
y = -radius *
cos(lerpDouble(0, (pi / sides), sides - sides.floor())! +
i * 2 * pi / sides);
} else {
x = radius *
sin(lerpDouble((pi / sides), 0, sides - sides.floor())! +
i * 2 * pi / sides);
y = -radius *
cos(lerpDouble((pi / sides), 0, sides - sides.floor())! +
i * 2 * pi / sides);
}
points.add(Offset(x, y));
}
return points;
}但是還是有些不完美,我還想讓多邊形邊數為偶數時,起始點是從最上方的邊的中點一直漸變到最上方的點
此時我們只需要將多邊形由偶數變為奇數時的起始點改為最上方邊線的中點即可。 此時代碼如下:
List<Offset> getPolygonPoints(double sides) {
for (int i = 0; i < sides.ceil(); i++) {
double x, y;
if (sides.ceil() % 2 == 0) {
if (sides.ceil() == sides) {
x = radius * sin((pi / sides) + i * 2 * pi / sides);
y = -radius * cos((pi / sides) + i * 2 * pi / sides);
} else {
x = radius *
sin(lerpDouble(0, (pi / sides), sides - sides.floor())! +
i * 2 * pi / sides);
y = -radius *
cos(lerpDouble(0, (pi / sides), sides - sides.floor())! +
i * 2 * pi / sides);
}
} else {
if (sides.ceil() == sides) {
x = radius * sin(i * 2 * pi / sides);
y = -radius * cos(i * 2 * pi / sides);
} else {
// 起始點位置單獨計算
if (i == 0) {
double startY = -radius * cos(pi / sides);
double endY = -radius;
x = 0;
y = lerpDouble(startY, endY, sides - sides.floor())!;
} else {
x = radius *
sin(lerpDouble((pi / sides), 0, sides - sides.floor())! +
(i - lerpDouble(1, 0, sides - sides.floor())!) *
2 *
pi /
sides);
y = -radius *
cos(lerpDouble((pi / sides), 0, sides - sides.floor())! +
(i - lerpDouble(1, 0, sides - sides.floor())!) *
2 *
pi /
sides);
}
}
}
points.add(Offset(x, y));
}
return points;
}在這個基礎上再畫出對角線,加上縮放,就能達到我們一開始看到的最終效果了。
感謝各位的閱讀,以上就是“怎么使用Flutter繪制分數邊形及多邊形漸變動畫”的內容了,經過本文的學習后,相信大家對怎么使用Flutter繪制分數邊形及多邊形漸變動畫這一問題有了更深刻的體會,具體使用情況還需要大家實踐驗證。這里是億速云,小編將為大家推送更多相關知識點的文章,歡迎關注!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。