您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要講解了“C++稀疏矩陣怎么實現”,文中的講解內容簡單清晰,易于學習與理解,下面請大家跟著小編的思路慢慢深入,一起來研究和學習“C++稀疏矩陣怎么實現”吧!
Q:什么是矩陣
A:數學上,一個矩陣由 m 行 n 列的元素組成,是一個 m 行,n 列的表,m 和 n 是矩陣的維度。一般地,寫作 mxn(讀作“m乘n”)來指明一個 m 行 n 列矩陣。矩陣的元素個數總計為 mn 個。如果 m 等于 n ,矩陣為方陣。

一般情況下,矩陣的標準存儲方式是一個二維數組 a[MAX_ROWS][MAX_COLS] 。利用這種存儲方式,可以通過 a[i][j] ,通過行下標,列下標快速找到任意元素的存儲位置。
Q:什么是稀疏矩陣
A:一個矩陣的絕大部分都為零元素,我們把這種矩陣稱為稀疏矩陣。
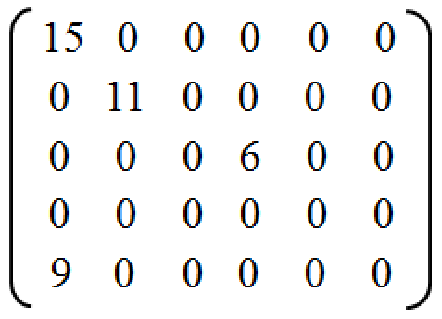
如圖:矩陣中只有 2/15 是非零元素,這就是一個標準的稀疏矩陣
Q:二維數組儲存矩陣的缺點
A:如果一個矩陣中包含很多零元素(是稀疏矩陣),就會浪費大量的存儲空間。因此,稀疏矩陣的存儲表示只需存儲非零元素。
Q:稀疏矩陣的存儲方式
A:通過對矩陣的分析,我們發現使用三元組 <row,col,value> 能夠唯一的刻畫矩陣的任意一個元素。這意味者可以使用三元數組來存儲表示稀疏矩陣。
代碼演示
#define MAX_TERMS 101 //定義最大長度
typedef struct{
int col;
int row;
int xalue;
}term;
term a[MAX_TERMS];我們可以用 a[0].row 表示行的數目,用 a[0].col 表示列的數目,用 a[0].value 表示非零元素的總數。其他位置 row 域存放行下標, col 域存放列下標,value 域存放元素值。三元組按照行的順序排序,并且在同一行內按照列的順序排序。
稀疏矩陣存儲為三元組
| 行 | 列 | 值 | |
|---|---|---|---|
| a[0] | 5 | 6 | 4 |
| a[1] | 0 | 0 | 15 |
| a[2] | 1 | 1 | 11 |
| a[3] | 2 | 3 | 6 |
| a[4] | 4 | 0 | 9 |
為了轉置一個矩陣,必須交換它的行和列。也就是說,原矩陣的任意元素 a[i][j] 應該成為其轉置矩陣的元素 b[j][i]
依次循環每一列,找到每一列的所有元素并把他們儲存在轉置矩陣的對應的行上。
//偽代碼
for 對于 j 列的所有元素
把元素<i,j,value>放置在元素<j,i,value>中
代碼演示
void transpose(term a[],term b[])
//b是a的轉置
{
int n,i,j,currentb;
n=a[0].value; //元素總數
b[0].row=a[0].col; //b的行數=a的列數
b[0].co 1=a[0].row; //b的列數=a的行數
b[0].value =n;
if(n> 0)
{// 非零矩陣
currentb=1;
for(i=0;i<a[0].col;i++)
//按a的列轉置
for(j=1;j<=n;j++)
//找出當前列的所有元素
if(a[j].col==i)
{//元素是當前列的,加入b
b[currentb]. row=a[j]. col;
b[currentb]. col=a[j]. row;
b[currentb]. value=a[j]. value;
currentb++;
}
}
}首先確定原矩陣中每一列的元素個數,這也就是其轉置矩陣中每一行的元素個數。于是就可以得到轉置矩陣每行的起始位置,從而,可以將原矩陣的元素依次移到其轉置矩陣中的恰當位置。
代碼演示
void fast transpose(term a[], term b[])
{
//將a的轉置矩陣存放于b中
int row terms[MAX_COL], starting pos[MAX_COL];
int i,j, num_cols=a[0].col, num_terms=a[0].value;
b[0].row=num_cols;b[0].col=a[0].row;
b[0].value=num_terms;
if(num_terms>0){//非零矩陣
for(i=0;i<num_cols;i++)
row_terms[i]=0;
for(i=1;i<=num_terms;i++)
row_terms[a[i]. co]]++;
starting_pos[0]=1;
for(i=1;i<num cols;i++)
starting_pos[i]=starting_pos[i-1]+row_terms[i-l];
for(i=1;i<=num_terms;i++){
j=starting_pos[a[i].col]++;
b[j].row=a[i].col;b[j].col=a[i].row;
b[j].value=a[i].value;
}
}
}Q:什么是矩陣乘法
A:設A為 mxp 的矩陣,B為 pxn 的矩陣,那么稱 mxn 的矩陣D為矩陣A與B的乘積,記作D=AB,其中矩陣D中的第 i 行第 j 列元素可以表示為:
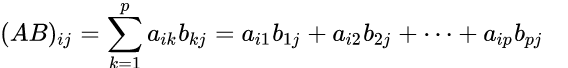
注意:兩個稀疏矩陣的乘積可能不再是稀疏矩陣
我們可以按照行的順序計算D的元素,把元素存放到正確的位置,這樣就不用移動已計算出的元素的位置。一般情況下,必須遍歷整個B才能得到第 j 列的所有元素。但是,我們可以先計算 B 的轉置,使列元素順序相續排序,可以避免重復多次遍歷整個 B 。
對于找出的 A 的第 i 行和 B 的第 j 列的所有元素,做合并操作就能實現矩陣乘法。
代碼演示
void storesum(term a[],int *totald,int row,int column,int *sum)
{//如果 *sum!=0,它的行和列存儲位置為 d 中的 *totald+1
if(*sum)
if(*tptald<MAX_TERMS)
{
d[++*totald].row=row;
d[*totald].col=column;
d[*totald].value=*sum;
*sum=0;
}
else{
fprintf(stderr,"Numbers of terms in product exceeds %d\n",MAX_TERMS);
exit(1);
}
}
void mmult(term a[], term b[], term d[])
//將兩個稀疏矩陣相乘
{
int i,j,column,totalb=b[0].value,totald=0;
int rows_a=a[0].row,cols_a=a[0].col;
totala=a[0].value;int cols_b=b[0].col;
int row_begin=1, row=a[1].row, sum=0;
int new_b[MAX-TERMS][3];
if(cols_a!=b[0].row){
fprintf(stderr,"Incompatible matrices\n");
exit(1);
}
fast_transpose(b.new_b);
//設置邊界條件
a[totala+1].row=rows_a;
new_b[totalb+1].row=cols_b;
new_b[totalb+1].col=0;
for(i=1;i<=totala;){
column=new_b[1].row;
for(j=1;j<=totalb+1;){
//將a的行乘以b的列
if(a[i].row!=row){
storesum(d,&totald,row,column,&sum);
i=row_begin;
for(;new_b[j].row==column;j++)
;
column=new_b[j]. row;
}
else if(new_b[j].row!=column){
storesum(d,&totald,row,column,&sum);
i=row_begin;
column=new_b[j].row;
}
else switch(COMPARE(a[i].col,new_b[j].col)){
case-1://轉到a中的下一項
i++;break;
case 0://添加項,轉到a和b的下一項
sum+=(a[i++].value*new_b[j++].value); break;
case 1://來到b的下一項
j++;
}
}// for j<=totalb+1 結束循環
for(;a[i].row==row;i++)
;
row_begin=i;row=a[i].row;
}//for i<=totala 結束循環
d[0].row=rows_a;
d[0].col=cols_b;d[0].value=totald;
}感謝各位的閱讀,以上就是“C++稀疏矩陣怎么實現”的內容了,經過本文的學習后,相信大家對C++稀疏矩陣怎么實現這一問題有了更深刻的體會,具體使用情況還需要大家實踐驗證。這里是億速云,小編將為大家推送更多相關知識點的文章,歡迎關注!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。