Java數據結構之線索化二叉樹怎么實現

這篇文章主要介紹“Java數據結構之線索化二叉樹怎么實現”，在日常操作中，相信很多人在Java數據結構之線索化二叉樹怎么實現問題上存在疑惑，小編查閱了各式資料，整理出簡單好用的操作方法，希望對大家解答”Java數據結構之線索化二叉樹怎么實現”的疑惑有所幫助！接下來，請跟著小編一起來學習吧！

1.線索化二叉樹的介紹

將數列 {1, 3, 6, 8, 10, 14 } 構建成一顆二叉樹.

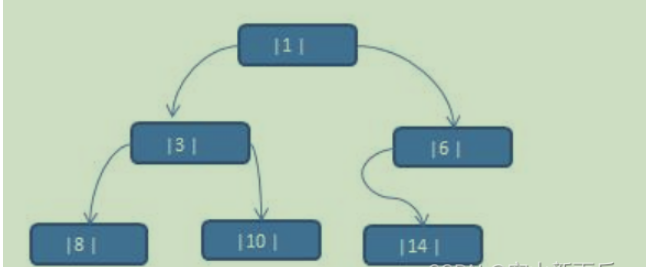
問題分析:

1.當我們對上面的二叉樹進行中序遍歷時，數列為 {8, 3, 10, 1, 6, 14 }

2.但是 6, 8, 10, 14 這幾個節點的 左右指針，并沒有完全的利用上.

3.如果我們希望充分的利用 各個節點的左右指針， 讓各個節點可以指向自己的前后節點,怎么辦?

4.解決方案-線索二叉樹

概念：當用二叉鏈表作為二叉樹的存儲結構時，可以很方便的找到某個結點的左右孩子；但一般情況下，無法直接找到該結點在某種遍歷序列中的前驅和后繼結點。所以使用線索化，利用二叉樹結構鏈表的空指針域進行線索化。

2.線索化二叉樹的基本特點

n 個結點的二叉鏈表中含有 n+1 【公式 2n-(n-1)=n+1】 個空指針域。利用二叉鏈表中的空指針域，存放指向該結點在某種遍歷次序下的前驅和后繼結點的指針（這種附加的指針稱為"線索"）

這種加上了線索的二叉鏈表稱為線索鏈表，相應的二叉樹稱為線索二叉樹(Threaded BinaryTree)。根據線索性質的不同，線索二叉樹可分為前序線索二叉樹、中序線索二叉樹和后序線索二叉樹三種

3.線索化二叉樹的應用案例

中序線索化二叉樹并遍歷

應用案例說明：將下面的二叉樹，進行中序線索二叉樹。中序遍歷的數列為 {8, 3, 10, 1, 14, 6}

思路分析

中序遍歷的結果：{8, 3, 10, 1, 14, 6}

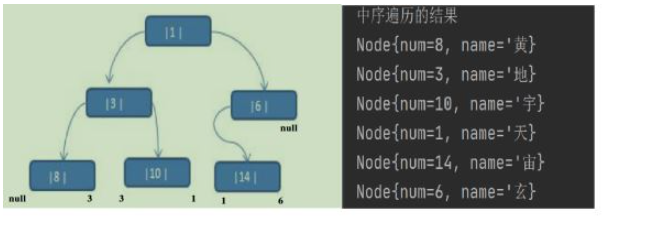
那么線索化之后的二叉樹的左右指針如上圖↑

說明: 當線索化二叉樹后，Node 節點的 屬性 left 和 right ，有如下情況:

• left 指向的是左子樹，也可能是指向的前驅節點. 比如 ① 節點 left 指向的左子樹, 而 ⑩ 節點的 left 指向的 就是前驅節點.

• right 指向的是右子樹，也可能是指向后繼節點，比如 ① 節點 right 指向的是右子樹，而⑩ 節點的 right 指向的是后繼節點.

因此要改變原來的二叉樹的結點結構

package com.studySelf.tree.threadedBinaryTree;

/**
 * @author wang
 * @version 1.0
 * @packageName com.studySelf.tree.tree01
 * @className Node
 * @date 2022/4/19 20:15
 * @Description Node結點
 */
public class Node {
    //唯一編號
    private int num;
    //結點的值
    private String name;
    //左結點
    private Node left;
    //右節點
    private Node right;

    //這個屬性用來控制線索二叉樹的結點的指向，0代表指向左結點，1代表指向前趨結點
    private int leftType;
    //這個屬性用來控制線索二叉樹的結點的指向，0代表指向右結點，1代表指向后繼結點
    private int rightType;


    //構造方法

    public Node(int num, String name) {
        this.num = num;
        this.name = name;
    }

    public int getLeftType() {
        return leftType;
    }

    public void setLeftType(int leftType) {
        this.leftType = leftType;
    }

    public int getRightType() {
        return rightType;
    }

    public void setRightType(int rightType) {
        this.rightType = rightType;
    }

    public int getNum() {
        return num;
    }

    public void setNum(int num) {
        this.num = num;
    }

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

    public Node getLeft() {
        return left;
    }

    public void setLeft(Node left) {
        this.left = left;
    }

    public Node getRight() {
        return right;
    }

    public void setRight(Node right) {
        this.right = right;
    }

    @Override
    public String toString() {
        return "Node{" +
                "num=" + num +
                ", name='" + name +
                '}';
    }

    /**
     * 前序遍歷
     */
    public void preSelect() {
        //首先輸出根結點
        System.out.println(this);
        //其次判斷是否有左結點
        if (this.left != null) {
            //沒有左結點，就遞歸調用本方法輸出該結點。
            this.left.preSelect();
        }
        if (this.right != null) {
            this.right.preSelect();
        }
    }

    /**
     * 中序遍歷
     */
    public void infixSelect() {
        //首先判斷左結點
        if (this.left != null) {
            //如果左結點不為空，遞歸向左子樹調用
            this.left.infixSelect();
        }
        //當左結點為空，再輸出根結點。當他本身就是最后一個左結點的時候，會直接輸出，且沒有右節點
        System.out.println(this);
        if (this.right != null) {
            //右節點同樣如此，遞歸調用。直到沒有結點為止。
            this.right.infixSelect();
        }
    }

    /**
     * 設二叉樹有三個結點，根結點，左結點，右節點。
     * 后序遍歷,解釋，當一個二叉樹的左結點不為空，那么他會進入下一個遞歸調用自己的后序遍歷方法
     * 此時，根結點就是左結點，這時判斷左結點，右節點均為空，就會輸出左結點
     * 回退到根結點為this的時候，左結點已經判斷完畢，接下來是右節點，右節點不為空，進入后續遍歷遞歸，
     * 此時的this就是右節點，進入遞歸后，判斷，不存在左右結點，輸出this，也就是整個二叉樹的右節點
     * 回退到this為根結點時，右節點也已經輸出，走到最后一步，輸出自己也就是this。
     * 整個后序遍歷就結束，那么該二叉樹的遍歷結果就是左，右，根
     */

    public void afterSelect() {
        if (this.left != null) {
            this.left.afterSelect();
        }

        if (this.right != null) {
            this.right.afterSelect();
        }
        System.out.println(this);
    }

    /**
     * @param num
     * @Date 2022/4/21 17:51
     * @Param
     * @Return Node
     * @MetodName preSearchByNum
     * @Author wang
     * @Description 根據結點的編號來查詢結點, 前序遍歷查詢，根，左，右
     */
    public Node preSearchByNum(int num) {
        //首先判斷傳進來的num與該結點的num是否相等
        //如果相等，那該結點就是我們要找的結點。
        if (this.num == num) {
            return this;
        }

        //如果不相等，該結點就不是我們要找的結點
        //那么我們就遍歷該結點的左子節點，和右子結點
        //定義一個結點用于接收最后的返回結果
        Node resultNode = null;
        //如果該結點的左子結點不為空，就遞歸調用前序遍歷，繼續查找，如果找到了，那么resultNode就是我們想要的值
        if (this.left != null) {
            resultNode = this.left.preSearchByNum(num);
        }

        //如果遍歷完左子結點，已經找到了我們想要的結果，直接返回結果即可，
        if (resultNode != null) {
            return resultNode;
        }

        //如果左子結點為空，且沒有找到我們想要的結點的情況下。那就判斷右子結點
        if (this.right != null) {
            resultNode = this.right.preSearchByNum(num);
        }
        //最后，如果找到了，那么resultNode一定會被賦值，如果沒找到，就會返回null
        return resultNode;
    }

    /**
     * @param num
     * @Date 2022/4/21 17:58
     * @Param
     * @Return Node
     * @MetodName infixSearchByNum
     * @Author wang
     * @Description 中序遍歷查找，左，根，右進行查詢即可。
     */
    public Node infixSearchByNum(int num) {
        //首先判斷左子結點,如果存在左子結點，遞歸繼續查詢遍歷即可即可。
        Node resultNode = null;
        if (this.left != null) {
            resultNode = this.left.infixSearchByNum(num);
        }

        //如果左子結點已經找到了我們想要的結點，直接返回當前結點即可
        if (resultNode != null) {
            return resultNode;
        }

        //判斷根結點
        if (this.num == num) {
            return this;
        }

        //判斷右子結點，
        if (this.right != null) {
            resultNode = this.right.infixSearchByNum(num);
        }
        //最后返回我們的結果即可。
        return resultNode;
    }


    /**
     * @param num
     * @Date 2022/4/21 19:15
     * @Param
     * @Return Node
     * @MetodName afterSearchNum
     * @Author wang
     * @Description 后續遍歷結點進行查找結點。左，右，根
     */
    public Node afterSearchNum(int num) {
        Node resultNode = null;
        //首先遍歷左結點
        if (this.left != null) {
            resultNode = this.left.afterSearchNum(num);
        }

        //判斷左結點是否找到哦啊
        if (resultNode != null) {
            return resultNode;
        }

        //判斷右節點是否為空
        if (this.right != null) {
            resultNode = this.right.afterSearchNum(num);
        }

        //判斷右節點是否找到
        if (resultNode != null) {
            return resultNode;
        }

        //判斷根結點是否為我們找的結點
        if (this.num == num) {
            return this;
        }
        //最后返回
        return resultNode;
    }

    /**
     * @param num
     * @Date 2022/4/25 19:30
     * @Param
     * @Return void
     * @MetodName delNodeByNum
     * @Author wang
     * @Description 根據結點的編號刪除結點
     */
    public void delNodeByNum(int num) {
        //首先，判斷當前結點的左結點是否為空，并且左結點的num是否與num相等
        if (this.left != null && this.left.num == num) {
            //如果相等，那就說明該結點就是我們要刪除的結點,將其左結點置空即可
            this.left = null;
            return;
        }

        //如果左結點沒有執行，說明左結點沒有我們想要的結果，也就是要刪除的結點不在左結點
        //那么就對右節點進行判斷
        if (this.right != null && this.right.num == num) {
            this.right = null;
            return;
        }

        //如果左右結點均沒有找到目標結點
        //那么就對左子樹進行遞歸刪除操作
        if (this.left != null) {
            this.left.delNodeByNum(num);
        }

        //同理，如果左子樹沒有目標結點，向右子樹進行遞歸刪除操作
        if (this.right != null) {
            this.right.delNodeByNum(num);
        }

    }
}

可以看到我們多出來了這么兩個屬性：

    //這個屬性用來控制線索二叉樹的結點的指向，0代表指向左結點，1代表指向前趨結點
    private int leftType;
    //這個屬性用來控制線索二叉樹的結點的指向，0代表指向右結點，1代表指向后繼結點
    private int rightType;

中序線索化二叉樹

  /**中序線索化二叉樹*/
    /**
     * @param node 該結點為根結點，從根節點開始線索化二叉樹，中序
     */
    public void infixThreadNodes(Node node) {
        /**首先判斷二叉樹的根節點上會否為空，如果根結點為空，不可以線索化，因為沒有二叉樹*/
        if (node == null) {
            return;
        }

        /**接著對左子樹進行線索化*/
        infixThreadNodes(node.getLeft());

        /**對當前結點進行線索化*/
        /**首先判斷當前結點的左子結點是否為空*/
        if (node.getLeft() == null) {
            //如果左子結點為空，說明就找到了我們需要線索化的結點
            //就可以將pre也就是一直在當前結點的前趨結點設置給當前結點的左子結點，
            //如果這是第一個結點，那么pre為空，正好第一個結點的前趨結點也為空
            node.setLeft(pre);
            //并且將它的左子結點的類型設置為前趨結點。1代表前趨結點
            node.setLeftType(1);
        }

        /**接著判斷前趨結點的右子結點是否為空，前提是前趨結點不能為空，如果他為空，說明這是第一個結點還沒走完*/
        if (pre != null && pre.getRight() == null) {
            //如果條件滿足，說明前趨結點現在已經走到了值，并且還沒有線索到后繼結點，
            // 也就是當前結點的上一個結點（這個上一個結點就是當前的前趨結點）還沒有后繼，
            //那么上一個結點的后繼結點就是當前結點，因此賦值前趨結點（也就是上一個結點）的后繼結點為當前結點。
            //這樣這條線索就連接上了,并且只有滿足葉子結點的結點才可以進行線索化
            pre.setRight(node);
            pre.setRightType(1);
        }

        //當前兩步走完之后，就可以將pre結點賦值為當前結點，
        // 因為下一個結點一走，當前結點就是前趨結點了。直到走到全部線索化結束
        //這步十分重要，這一步不寫，整個線索化就連接不上
        pre = node;

        /**對右子樹進行線索化*/
        infixThreadNodes(node.getRight());
    }

中序線索化二叉樹思路

1. 因為中序遍歷的二叉樹順序是左根右，因此，首先對左子樹進行線索化，遞歸線索化即可；

2. 當遞歸到左子樹的最左結點的時候，他的左結點肯定為空，那么就對他的左結點賦值為pre（pre結點是在線索化的最后一步賦值為當前結點，這樣遞歸才能進行下去）,注意左結點的類型一定要改為1，代表他是前趨結點。前趨結點就線索掉了。

3. 后繼結點的處理則是判斷前趨結點，當前趨結點不為空，并且前趨結點的右節點為空，那么設置前趨結點的右節點為當前結點，也就是上一個結點未設置的右節點，類型同樣要設置為后繼

4. 最后就是對pre這個結點賦值，為當前結點，因為下一次遞歸，當前結點就成了上一個結點，也就是這里的pre

5. 最后就是對二叉樹的右子結點進行線索化。

中序線索化二叉樹的遍歷

1. 遍歷中序線索化二叉樹首先應該明確的是他的遍歷順序要和遍歷原來的中序二叉樹遍歷的結果是一樣的，才是遍歷成功

2. 那么第一步應該就是判斷根結點不為空，也就是循環結束條件

3. 接著就循環查找當前結點的左子結點類型為0的也就是沒有被線索化的結點，只要他為0，那么結點就一直往左子結點賦值。直到找到第一個被線索化的結點，輸出他，他就是我們第一個線索化并且也是中序遍歷的第一個左子結點。

4. 輸出之后，判斷他的右子結點是否被線索化，如果被線索化，那么當前結點node就被賦值為它自己的右子結點，并且輸出，如果他之后的結點的右子結點的類型又為1，那么繼續往后走并賦值，說明他有后繼

5. 直到右子結點的類型為0，退出循環之后，也應該向右再賦值，繼續向后遍歷

代碼演示

    /**遍歷中序線索化二叉樹*/
    public void infixThreadNodesSelect() {
        /**第一個結點為根結點*/
        Node node = root;
        while(node != null) {
            /**當結點不為空，就一直遍歷*/
            /**當該結點的左子結點的類型為1的時候，也就是說該結點是被線索化的結點,
             * 因為是中序遍歷，所以應該遍歷到最左邊的最左子結點，那么就是第一個
             * 左子結點類型為1的結點。*/
            while(node.getLeftType() == 0) {
                node = node.getLeft();
            }
            /**當左子結點的類型為1,輸出左子結點*/
            System.out.println(node);

            /**當右子結點類型為1，當前結點輸出完畢后
             * 中序遍歷就應該輸出右子結點，那么就是當前結點的右子結點類型只要為1，就往后移動
             * 并且輸出，當他為0，說明沒有線索化，那么沒有后繼結點，但是他有右子結點，
             * 因此要在循環結束以后向后移動。*/
            while (node.getRightType() == 1) {
                node = node.getRight();
                System.out.println(node);
            }
            /**當右子結點循環退出，說明這里到了類型為0也就是后繼結點*/
            node = node.getRight();
        }

4.前序線索化二叉樹、遍歷

線索化二叉樹

 /**
     * 前序線索化二叉樹
     */
    public void preThreadNodes(Node node) {
        /**首先判斷當前節點是否為空*/
        if (node == null) {
            return;
        }

        /**如果是前序遍歷，那么先對當前結點進行判斷，當前結點的前趨結點的操作*/
        if (node.getLeft() == null) {
            node.setLeft(pre);
            node.setLeftType(1);
        }

        /**處理后繼結點,定義的前趨結點不為空，說明他有值，就是已經存在了上一個結點的值，他的右子結點沒有值的話，就可以
         * 給他賦予后繼結點為當前結點，這里賦予的也就是上一個結點*/
        if (pre != null && pre.getRight() == null) {
            pre.setRight(node);
            pre.setRightType(1);
        }

        /**這里是關鍵的一步*/
        pre = node;

        /**對左子結點進行線索化,注意，這里需要排除已經被線索化掉的結點,因為這里要考慮一個情況，
         * 比如這里已將到了最下面一個左子結點，由于是前序遍歷，遍歷到左子結點，他的前趨結點在上面就設置了
         * 如果這里不判斷左子結點的類型，那么就會進入遞歸，但是這個遞歸如果進去了，就是錯誤的遞歸，因為他傳過去的結點
         * 是我們剛剛給他賦值的前趨結點，也就是根結點。會發生錯誤。因此得判斷類型*/
        if (node.getLeftType() != 1) {
            preThreadNodes(node.getLeft());
        }


        /**對右子結點進行遞歸線索化*/
        if (node.getRightType() != 1) {
            preThreadNodes(node.getRight());
        }
    }

 遍歷線索化二叉樹

/**
     * 前序遍歷線索二叉樹*/
    public void preThreadNodeSelect() {
        Node node = root;
        while(node !=null) {
            while(node.getLeftType() == 0) {
                /**前序遍歷為根左右，先輸出根結點,因為他每次進來循環肯定是先到根結點，所以一進該循環
                 * 就要輸出根結點，當他的lefttype=1循環結束，說明遇到了被線索化的地方了。*/
                System.out.println(node);
                /**再最左子結點進行遍歷*/
                node = node.getLeft();
            }
            /**上面的循環結束之后就應該輸出當前結點，也就是那個序列化的結點
             * 之后結點向右移動繼續遍歷*/
            System.out.println(node);
            node = node.getRight();
        }
  }

圖解

5.后序線索化二叉樹

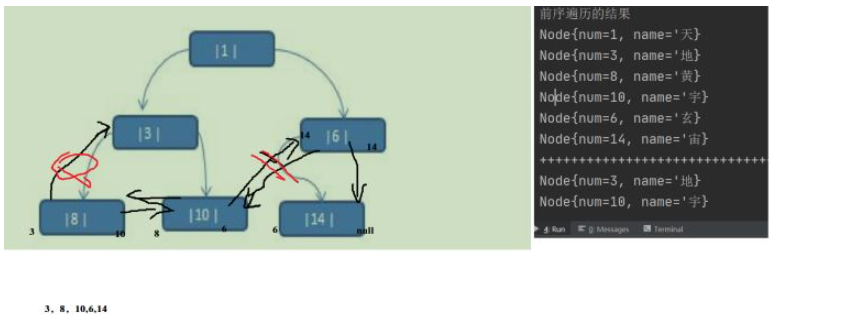
后續線索化二叉樹

/**
 * 后序線索化二叉樹的方法
 */
public void postThreadedBinaryTree(Node node) {
    /**首先判斷結店不能為空*/
    if (node == null) {
        return;
    }

    /**先后續線索化左子結點*/
    postThreadedBinaryTree(node.getLeft());
    /**在后續線索化右子結點*/
    postThreadedBinaryTree(node.getRight());

    /**處理當前結點的前趨結點*/
    if (node.getLeft() == null) {
        node.setLeft(pre);
        node.setLeftType(1);
    }

    /**處理后繼結點*/
    if (pre != null && pre.getRight() == null) {
        pre.setRight(node);
        pre.setRightType(1);
    }
    pre = node;
}

到此，關于“Java數據結構之線索化二叉樹怎么實現”的學習就結束了，希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習，快去試試吧！若想繼續學習更多相關知識，請繼續關注億速云網站，小編會繼續努力為大家帶來更多實用的文章！