您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容主要講解“Javascript數據結構之棧和隊列怎么實現”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“Javascript數據結構之棧和隊列怎么實現”吧!
棧是一種具有 「后入先出」(Last-in-First-Out,LIFO) 特點的抽象數據結構。
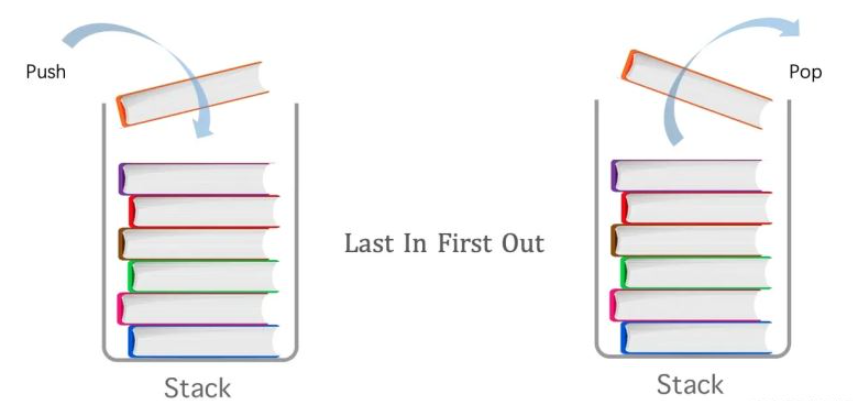
了解棧的樣子,最常見的例子如:一摞盤子、一個壓入子彈的彈夾。還有比如我們上網使用的瀏覽器,都有『后退』、『前進』按鈕。后退操作,就是把當前正在瀏覽的頁面(棧頂)地址出棧,倒退回之前的地址。我們使用的編輯類的軟件,比如 IDE,Word,PhotoShop,他們的撤銷(undo)操作,也是用棧來實現的,軟件的具體實現代碼可能會有比較大的差異,但原理是一樣的。
由于棧后入先出的特點,每次只能操作棧頂的元素,任何不在棧頂的元素,都無法訪問。要訪問下面的元素,先得拿掉上面的元素。所以它是一種高效的數據結構。
用 Javascript 實現一個棧,通常我們用數組就可以。可以做一個簡單的封裝。
棧通常需要實現下面常用功能:
push(插入新元素,并讓新元素成為棧頂元素)
pop(棧頂元素出棧,并返回棧頂元素)
peek(想知道棧最后添加的是哪個,用這個方法。返回棧頂元素,不出棧。是個輔助方法)
clear(清空棧)
isEmpty(若棧為空,返回 true,否則返回 false)
size(返回棧元素個數)
class Stack {
constructor() {
this.items = [];
}
push(item) {
this.items.push(item);
}
pop() {
return this.items.pop();
}
peek() {
return this.items[this.items.length - 1];
}
clear() {
this.items = [];
}
isEmpty() {
return this.items.length === 0;
}
size() {
return this.items.length;
}
}
const stack = new Stack();
stack.push('c++');
stack.push('swift');
stack.push('python');
stack.push('javascript');
console.log(stack.isEmpty()); // false
console.log(stack.size()); // 4
console.log(stack.peek()); // javascript
const removedItem = stack.pop();
console.log(removedItem); // javascript
console.log(stack.peek()); // python
stack.clear();
console.log(stack.isEmpty()); // true
console.log(stack.size()); // 0那么棧如何應用解決實際問題,下面是一個例子。
一個十進制轉換為二進制的例子:
function transitionToBin(decNumber) {
const stack = new Stack();
do {
// 每次循環計算出的低位值,依次入棧
stack.push(decNumber % 2);
decNumber = Math.floor(decNumber / 2);
} while(decNumber > 0);
let result = '';
// 此時,stack 中存放的是轉換后二進制值,棧頂是高位,依次向下。
while (stack.size() > 0) {
// 從棧頂的高位依次出棧,拼接到顯示結果中
result += stack.pop();
}
return result;
}
const binNumber = transitionToBin(321);
console.log('binNumber: ', binNumber);棧也被用于內存保存變量和方法調用。函數調用的時候壓棧,return 結果的時候,出棧。比如我們經常用的遞歸 (recursion) ,就是棧應用的例子。
比如下面一個計算階乘的例子:
function factorial(n) {
return n > 1 ? n * factorial(n - 1) : n;
}
console.log(factorial(4));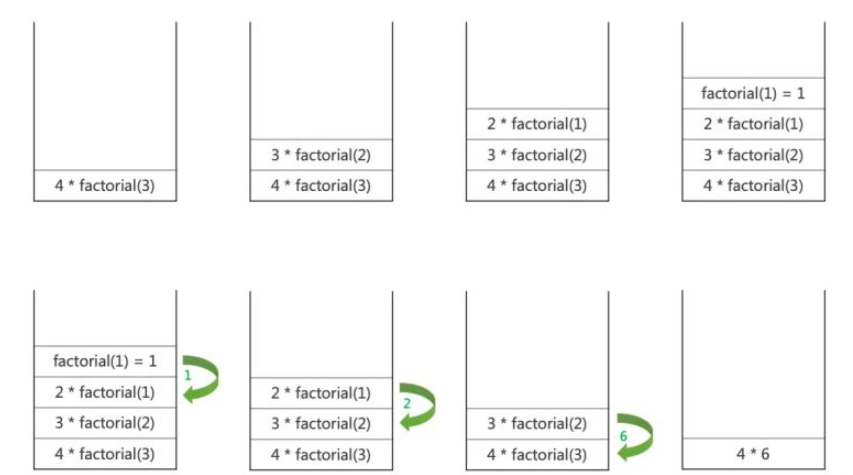
除了棧,隊列也是一種常用的數據結構。隊列是由順序元素組成的線性數據結構,又不同于棧 (Last-in-First-Out,LIFO) ,他遵循的是先進先出(First-In-First-Out,FIFO) 。
隊列在隊尾添加新元素,在頂部移除元素。
現實中,最常見的隊列例子就是排隊。
計算機中,隊列應用也相當廣泛。例如計算機 CPU 作業調度(Job Scheduling)、外圍設備聯機并發(spooling)、樹和圖的廣度優先搜索(BFS)

一個隊列數據結構,主要是要實現兩個操作:
enqueue 把一個新元素推入隊列
dequeue 從隊列中移除一個已有元素
我們創建一個類來封裝一個隊列。我們可以使用 javascript 原生的數組來存儲里面的數據內容,和 javascript 自帶的函數來實現隊列的操作。
class Queue {
constructor() {
this.items = [];
}
// 推入
enqueue(item) {
this.items.push(item);
}
// 移除
dequeue() {
return this.items.shift();
}
// 隊列頭元素
peek() {
return this.items[0];
}
// 為空判斷
isEmpty() {
return this.items.length === 0;
}
size() {
return this.items.length;
}
}我們在遍歷一顆樹的時候,可以使用棧思路進行深度優先遍歷,也可以采用隊列的思路,廣度優先遍歷。假設我們有下面這樣一個樹形的數據結構,我們查找它所有的節點值。
const treeData = {
node: {
value: 12,
children: [{
value: 30,
children: [{
value: 22,
children: null
}, {
value: 10,
children: [{
value: 5,
children: null
}, {
value: 4,
children: null
}]
}]
}, {
value: 6,
children: [{
value: 8,
children: null
}, {
value: 70,
children: null
}]
}]
}
};我們用隊列進行廣度優先的思路來遍歷。代碼和示意圖如下:
function bfs(tree) {
// 準備一個空的隊列
const queue = new Queue();
queue.enqueue(tree);
// 一個用于顯示結果的數組
const result = [];
do {
// 出隊列
let node = queue.dequeue();
result.push(node.value);
if (node.children && node.children.length > 0) {
node.children.forEach(sub => {
queue.enqueue(sub);
});
}
} while (queue.size() > 0);
// 顯示遍歷結果
console.log('result:', result.join(', '));
}
bfs(treeData.node);
// result: 12, 30, 6, 22, 10, 8, 70, 5, 4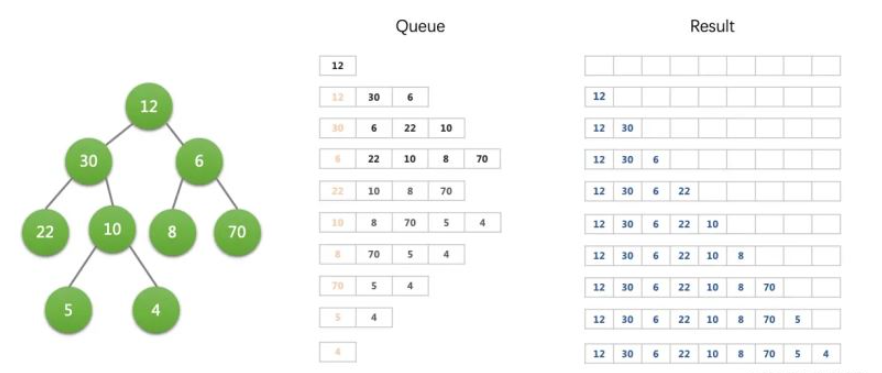
在實際情況中,有的隊列需要一些特殊的處理方式,出隊列規則的不一定是簡單粗暴的最早進入隊列最先出。 比如:
醫院對病人的分診,重癥的優先給予治療
我們銷售某件商品時,可以按照該商品入庫的進貨價作為條件,進貨價高的優先拿出銷售。
于是,就有了優先隊列。優先隊列是普通隊列的一種擴展,它和普通隊列不同的在于,隊列中的元素具有指定的優先級別(或者叫權重)。 讓優先級高的排在隊列前面,優先出隊。優先隊列具有隊列的所有特性,包括基本操作,只是在這基礎上添加了內部的一個排序。
因為設置了一些規則,我們可以用順序存儲的方式來存儲隊列,而不是鏈式存儲。換句話說,所有的節點都可以存儲到數組中。
滿足上面條件,我們可以利用線性數據結構的方式實現,但時間復雜度較高,并不是最理想方式
我們要實現優先隊列,就會有兩種方法。
第一種,就是插入的時候,不考慮其他,就在隊列末尾插入。而移除的時候,則要根據優先級找出隊列中合適的元素移除。
第二種是,插入元素的時候,根據優先級找到合適的放置位置,而移除的時候,直接從隊列前面移除。
下面以第二種情況為例,實現一個優先隊列:
class QItem {
constructor(item, priority) {
this.item = item;
this.priority = priority;
}
toString() {
return `${this.item} - ${this.priority}`;
}
}
class PriorityQueue {
constructor() {
this.queues = [];
}
// 推入
enqueue(item, priority) {
const q = new QItem(item, priority);
let contain = false;
// 這個隊列本身總是按照優先級,從大到小的
// 所以找到第一個比要插入值小的那個位置
for (let i = 0; i < this.queues.length; i++) {
if (this.queues[i].priority < q.priority) {
this.queues.splice(i, 0, q);
contain = true;
break;
}
}
// 都比它大,放最后
if (!contain) {
this.queues.push(q);
}
}
// 移除
dequeue() {
return this.queues.shift();
}
// 隊列頭元素
peek() {
return this.queues[0];
}
isEmpty() {
return this.queues.length === 0;
}
size() {
return this.queues.length;
}
}
const queue = new PriorityQueue();
queue.enqueue('K40', 3100);
queue.enqueue('K50', 5000);
queue.enqueue('K10', 6100);
queue.enqueue('K10', 6000);
queue.enqueue('K10', 5600);
queue.enqueue('K50', 4600);
queue.enqueue('K40', 5900);
console.log(queue.dequeue());
console.log(queue.dequeue());
console.log(queue.dequeue());
console.log(queue.dequeue());
console.log(queue.dequeue());
console.log(queue.dequeue());
console.log(queue.dequeue());
/*
QItem { item: 'K10', priority: 6100 }
QItem { item: 'K10', priority: 6000 }
QItem { item: 'K40', priority: 5900 }
QItem { item: 'K10', priority: 5600 }
QItem { item: 'K50', priority: 5000 }
QItem { item: 'K50', priority: 4600 }
QItem { item: 'K40', priority: 3100 }
*/上面是簡單的使用一個線性數據結構,實現了一個優先隊列。我們也可以用實現。這種堆數據存儲的時候也是一個線性的,只是這些數據的存放位置有一定規則。
堆可以理解為可以迅速找到一堆數中的最大或者最小值的數據結構
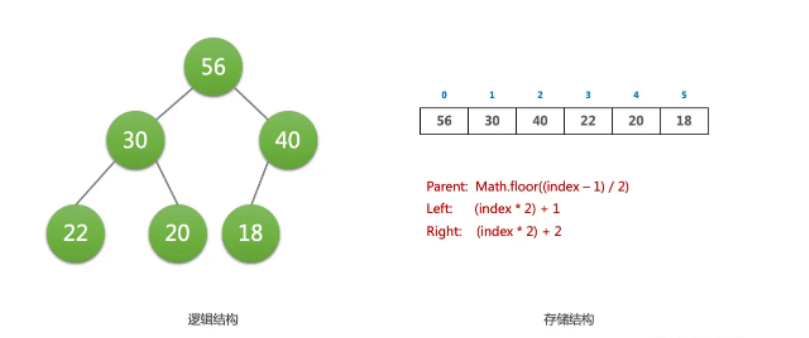
堆是具有特殊特征的完全二叉樹(也叫二叉堆)。
二叉堆特點:
它是一個完全二叉樹(complete binary tree) 的數據結構。所謂完全二叉樹(complete binary tree),就是整個二叉樹,除了底層的葉子節點,其他的層都是填滿的,而且底層的葉子節點,從左到右不能有空的。(這樣一個完全二叉樹就能使用 Array 這種線性結構來存儲)
大頂堆(Max heap) :父節點的值大于或者等于子節點的值,堆頂是這個堆的最大元素
小頂堆(Min heap) :父節點的值小于或者等于子節點的值,堆頂是這個堆的最小元素
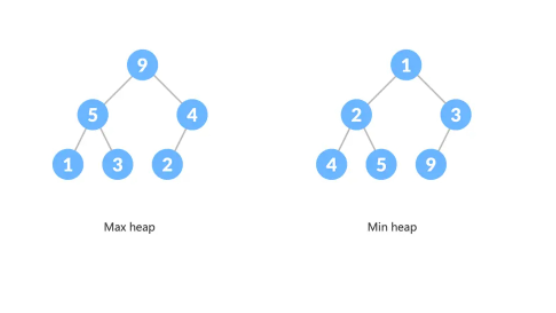
因為完全二叉樹的特性,我們可以用一個數組來存儲二叉堆
二叉堆是實現堆排序和優先隊列的基礎。二叉堆常用的應用場景就是優先隊列,它處理最大、最小值效率很高。同時堆排序算法也用到了二叉堆。
二叉堆的插入和刪除操作比較復雜,我們用 max-heap 舉例說明。
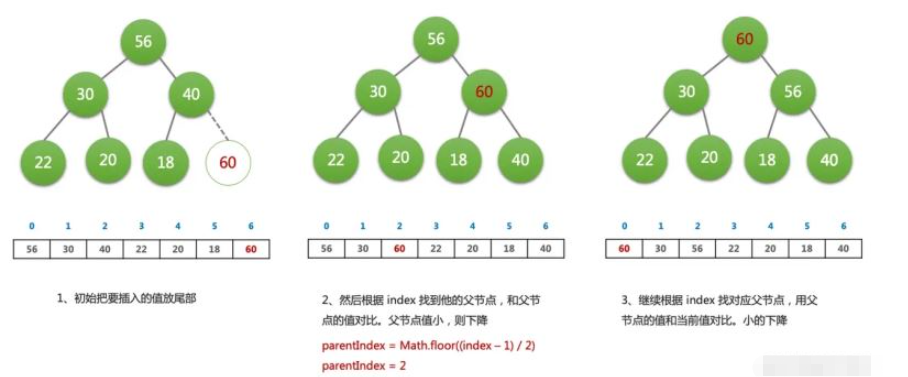
插入(enqueue)操作
新元素一律先插入到堆的尾部
依次向上調整整個堆的結構(一直到根即可)
HeapifyUp
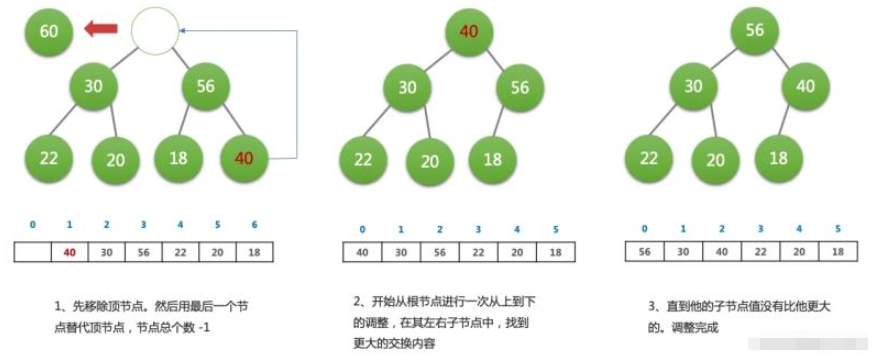
刪除(dequeue)操作
取出頂部元素(因為它永遠是最大那個)
將尾元素替換到頂部(先不用管它的大小)
依次從根部向下調整整個堆的結構(一直到堆尾即可)
HeapifyDown
下面是一個 max-heap 的實現。comparator 函數里面修改一下,就可以變成一個 min-heap
class Heap {
constructor(comparator = (a, b) => a - b) {
this.arr = [];
this.comparator = (iSource, iTarget) => {
const value = comparator(this.arr[iSource], this.arr[iTarget]);
if (Number.isNaN(value)) {
throw new Error(`Comparator should evaluate to a number. Got ${value}!`);
}
return value;
}
}
enqueue(val) {
// 插入到末尾
this.arr.push(val);
// 向上冒泡,找到合適位置
this.siftUp();
}
dequeue() {
if (!this.size) return null;
const val = this.arr.shift();
const rep = this.arr.pop();
this.arr.splice(0, 0, rep);
this.siftDown();
}
get size() {
return this.arr.length;
}
siftUp() {
// 新元素索引
let index = this.size - 1;
// 根據完全二叉樹的規則,這里我們可以依據元素索引index的值,獲得他對應父節點的索引值
const parent = (i) => Math.floor((i - 1) / 2);
if (parent(index) >= 0 && this.comparator(parent(index), index) < 0) {
// 如果父節點存在,并且對比值比當前值小,則交互位置
this.swap(parent(index), index);
index = parent(index);
}
}
siftDown() {
let curr = 0;
const left = (i) => 2 * i + 1;
const right = (i) => 2 * i + 2;
const getTopChild = (i) => {
// 如果右節點存在,并且右節點值比左節點值大
return (right(i) < this.size && this.comparator(left(i), right(i)) < 0)
? right(i) : left(i);
};
// 左節點存在,并且當前節點的值,小于子節點中大的那個值,交換
while (left(curr) < this.size && this.comparator(curr, getTopChild(curr)) < 0) {
const next = getTopChild(curr);
this.swap(curr, next);
curr = next;
}
}
// 交換位置
swap(iFrom, iTo) {
[this.arr[iFrom], this.arr[iTo]] = [this.arr[iTo], this.arr[iFrom]];
}
}
const heap = new Heap();
heap.enqueue(56);
heap.enqueue(18);
heap.enqueue(20);
heap.enqueue(40);
heap.enqueue(30);
heap.enqueue(22);
console.log('heapify: ', heap.arr.join(', '));
heap.dequeue();
console.log('step 1: ', heap.arr.join(', '));
heap.dequeue();
console.log('step 2: ', heap.arr.join(', '));
heap.dequeue();
console.log('step 3: ', heap.arr.join(', '));
// heapify: 56, 40, 22, 18, 30, 20
// step 1: 40, 30, 22, 18, 20
// step 2: 30, 20, 22, 18
// step 3: 22, 20, 18如上面代碼所示,數據進入隊列是無序的,但在出隊列的時候,總是能找到最大那個。這樣也實現了一個優先隊列。
Scheduler 存在兩個隊列,timerQueue(未就緒任務隊列) 和 taskQueue(就緒任務隊列)。當有新的未就緒任務被注冊,就會 push 到 timerQueue 中,并根據開始時間重新排列任務順序。
push 方法是在一個叫 schedulerMinHeap.js 的文件中基于最小堆(min-heap)來實現的。schedulerMinHeap 源碼
export function push(heap: Heap, node: Node): void {
const index = heap.length;
heap.push(node);
siftUp(heap, node, index);
}看到代碼中,在 push 之后,調用了 siftUp 來重新整理順序
function siftUp(heap, node, i) {
let index = i;
while (index > 0) {
const parentIndex = (index - 1) >>> 1;
const parent = heap[parentIndex];
if (compare(parent, node) > 0) {
// The parent is larger. Swap positions.
heap[parentIndex] = node;
heap[index] = parent;
index = parentIndex;
} else {
// The parent is smaller. Exit.
return;
}
}
}這里計算 parentIndex 是用了位移的方法(等價于除以 2 再去尾),帥!
到此,相信大家對“Javascript數據結構之棧和隊列怎么實現”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。