您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
今天小編給大家分享一下C語言數據結構堆排序示例分析的相關知識點,內容詳細,邏輯清晰,相信大部分人都還太了解這方面的知識,所以分享這篇文章給大家參考一下,希望大家閱讀完這篇文章后有所收獲,下面我們一起來了解一下吧。
什么是堆排序?假如給你下面的代碼讓你完善堆排序,你會怎么寫?你會怎么排?
void HeapSort(int* a, int n)
{
}
int main()
{
int arr[] = { 4,2,7,8,5,1,0,6 };
int sz = sizeof(arr) / sizoef(arr[0]);
HeapSort(arr, sz);
return 0;
}堆排序就是利用堆這個數據結構,對一組數據進行排序。
所以說,堆排序整體分兩步完成。
第一步,建堆
第二步,進行排序
注意:以下代碼針對的是對一組 數據 排升序
對的,向下調整方法,是最優秀的堆排序。
不是太想介紹那種向上調整拉胯的堆排序,我們經常用的是這種優秀的向下排序。
二者區別在于建堆的方法不同。一個是向下建堆O(N),一個是向上建堆O(N*logN)。
具體證明用到了高中 簡單的數列公式。
向下建堆也有兩種情況。
1.建大堆
2.建小堆
那么到底建大堆還是小堆呢?
解釋:建堆在于你是想要排升序,還是排降序。假如建的大堆,因為堆頂的數是最大的,在我們對堆 向下調整排序時,這時候每次都需要把最大的交換到堆底。所以導致最后堆的順序是升序。
建大堆前
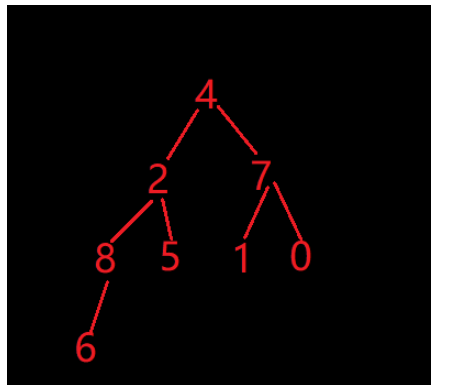
建大堆后

向下調整排序后
此時數組就有序了。

結論:實質是在數組上建堆。排升序建大堆,排降序建小堆。
思路:
因為葉子結點本身就是一個大堆,所以從最后一個葉子結點的父親結點開始進行向下建堆。
這樣就能夠保證每次建的堆都是大堆。
注意:
1.注意循環結束條件,和if語句里的邊界問題child + 1 < n
2.注意完全二叉樹父子關系公式
#include <stdio.h>
//交換
void swap(int* x, int* y)
{
int t = 0;
t = *x;
*x = *y;
*y = t;
}
//向下調整
void AdjustDown(int* a, int n, int root)
{
int parent = root;
int child = parent * 2 + 1;
while (child < n)
{
//每次調整都需要從左右兩邊選出孩子最大的那個
//假設坐孩子較大,選出左右孩子大的那個
if (child + 1 < n && a[child + 1] > a[child])
{
++child;
}
//開始調整。
if (a[child] > a[parent])
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
//不滿足就跳出,開始下次for循環調整。
else
{
break;
}
}
}
void HeapSort(int* a, int n)
{
//向下調整建堆
int i = 0;
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
}
int main()
{
int arr[] = { 4,2,7,8,5,1,0,6 };
int sz = sizeof(arr) / sizeof(arr[0]);
HeapSort(arr, sz);
return 0;
}1.從堆底依次 和 堆頂的數據進行交換。
2.對交換后的 堆頂的值 進行向下調整。向下調整時請無視交換到堆底那個最大的值。
3.繼續循環第一步和第二步,直到到正數第二個數結束。
void swap(int* x, int* y)
{
int t = 0;
t = *x;
*x = *y;
*y = t;
}
void AdjustDown(int* a, int n, int root)
{
int parent = root;
int child = parent * 2 + 1;
while (child < n)
{
//每次調整都需要從左右兩邊選出孩子最大的那個
//假設坐孩子較大,選出左右孩子大的那個
if (child + 1 < n && a[child + 1] > a[child])
{
++child;
}
//開始調整。
if (a[child] > a[parent])
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
//不滿足就跳出,開始下次for循環調整。
else
{
break;
}
}
}
void HeapSort(int* a, int n)
{
//向下調整建堆
int i = 0;
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
//向下調整排序
int end = 0;
for (end = n-1; end > 0; end--)
{
swap(&a[0], &a[end]);
//向下調整時無視最大的那個值,所以end是n-1。
AdjustDown(a, end, 0);
}
}
int main()
{
int arr[] = { 4,2,7,8,5,1,0,6 };
int sz = sizeof(arr) / sizeof(arr[0]);
HeapSort(arr, sz);
return 0;
}//向下調整建堆
int i = 0;
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}很多人的誤區在于他的時間復雜度是N*Log2N。這是錯誤的。
時間復雜度的計算是看思想,而不是看循環猜測。
當是滿二叉樹,在最壞的情況下,除了最后一層,上面所有層都需要進行向下調整。
最壞情況下的調整次數 = 每層數據個數 * 向下調整次數
第一層向下調整次數是h-1,節點個數是21-1
第二層向下調整次數是h-2, 節點個數是22-1
第h-1層向下調整次數是1,節點個數是2h-1-1
所以總的調整次數為n:n = 20*(h-1) + 21 *(h-2)+… + 2h-1-1 *(1)
根據高中錯位相減得到 n = 1−h+21+22+…+2h−2+2h−1
由等比數列前n項和得到 n = 2h−h−1
由二叉樹性質N=2h−1和 h = log2(N+1) 得到 n=N−log2(N+1)
大O漸進表示法為n= O(N)
需要向下調整n-1次。每次需要調整的高度為LogN,N為節點的個數,因為節點個數每次少一個。
所以n-1次調整總次數 = log2+log3+…+log(n-1)+log(n)≈log(n!)
由數學知識得log(n!)和nlog(n)是同階函數。
所以向下調整排序時間復雜度為N*LogN
所以堆排序時間復雜度為:N + N*LogN
大O漸進表示法為:O(N*LogN)
總結:堆排序時間復雜度 O(N*LogN)
向上調整排序和向下調整排序的唯一不同在于建堆的不同,導致二者的建堆的時間復雜度略微不同。
向上調整建堆時間復雜度為N*LogN.具體原因還需要經過殘酷的數學計算。孩子不會啊。但是經過網上查閱資料我又找到了計算方法。如圖。
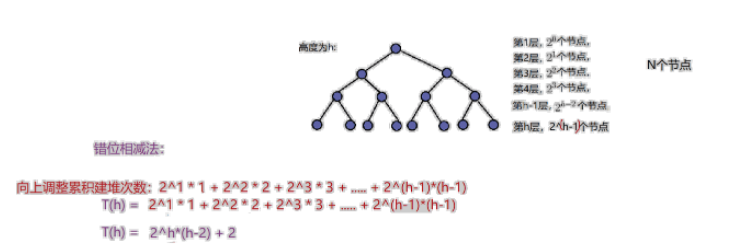
根據二叉樹的性質:h = Log2(N+1)
可以將T(h) = 2h * (h-2) + 2換為:
所以總體來說就是向上調整的建堆時間復雜度為O(N * LogN).
思路:從第二個元素開始,只關注前兩個元素建堆,然后再依次增加元素建堆,使它一直為堆。
向上調整建堆雖然時間復雜度略高,但是代碼相對于向下調整簡單一點點。
void AdjustUp(int* a, int child)
{
//先把父親節點表示出來。
int parent = (child - 1) / 2;
while (child > 0)
{
//比較孩子和父親,開始向上調整。
if (a[child] > a[parent])
{
swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}以上就是“C語言數據結構堆排序示例分析”這篇文章的所有內容,感謝各位的閱讀!相信大家閱讀完這篇文章都有很大的收獲,小編每天都會為大家更新不同的知識,如果還想學習更多的知識,請關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。