您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“C語言數據結構二叉樹遞歸的方法”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!
二叉樹的精髓在于遍歷。遍歷掌握了后,剩下的問題迎刃而解。
“工欲善其事必利其器”
1.所以先創建一個結構體。
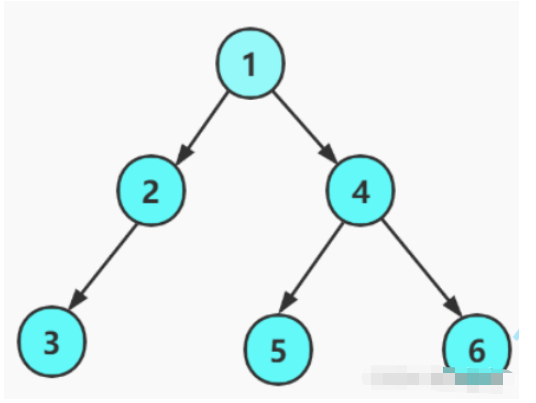
2.手動先構造一顆如圖所示的二叉樹。
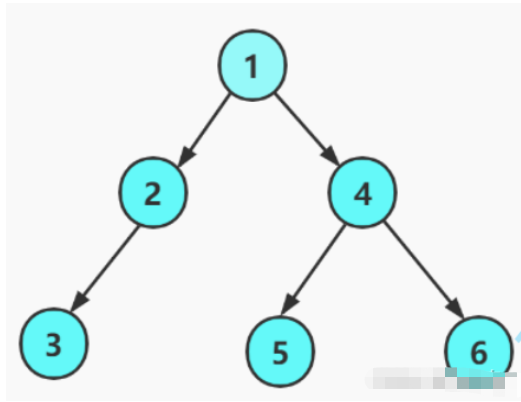
typedef int BTDataType;//定義二叉樹結構體typedef struct BinaryTreeNode{<!--{C}%3C!%2D%2D%20%2D%2D%3E-->int data;//節點數據struct BinartTreeNode* left;//左子樹struct BinartTreeNode* right;//右子樹}BTNode;//構造一棵二叉樹BTNode* BuyBTNode(BTDataType x){<!--{C}%3C!%2D%2D%20%2D%2D%3E-->BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){<!--{C}%3C!%2D%2D%20%2D%2D%3E-->printf("malloc fail\n");exit(-1);}node->data = x;node->left = NULL;node->right = NULL;return node;}BTNode* CreatBinaryTree(){<!--{C}%3C!%2D%2D%20%2D%2D%3E-->BTNode* node1 = BuyBTNode(1);BTNode* node2 = BuyBTNode(2);BTNode* node3 = BuyBTNode(3);BTNode* node4 = BuyBTNode(4);BTNode* node5 = BuyBTNode(5);BTNode* node6 = BuyBTNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;}int main(){<!--{C}%3C!%2D%2D%20%2D%2D%3E-->BTNode* tree = CreatBinaryTree();return 0;}typedef int BTDataType;
//定義二叉樹結構體
typedef struct BinaryTreeNode
{
int data;//節點數據
struct BinartTreeNode* left;//左子樹
struct BinartTreeNode* right;//右子樹
}BTNode;
//構造一棵二叉樹
BTNode* BuyBTNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
printf("malloc fail\n");
exit(-1);
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyBTNode(1);
BTNode* node2 = BuyBTNode(2);
BTNode* node3 = BuyBTNode(3);
BTNode* node4 = BuyBTNode(4);
BTNode* node5 = BuyBTNode(5);
BTNode* node6 = BuyBTNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
int main()
{
BTNode* tree = CreatBinaryTree();
return 0;
}
遍歷順序:根 左子樹 右子樹
思路:
1.把每個節點都想成是一棵樹。
2.當樹為空時。
3.當樹不為空時,先遍歷左子樹,后遍歷右子樹
注意:前中后序遍歷不同處只在printf打印的順序的位置。
// 二叉樹前序遍歷
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
//打印在前
printf("%d ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}打印結果:
1 2 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL
遞歸分析圖:
遞歸題目的萬能的解法。就是畫遞歸圖。
二叉樹的所有題目,假如你不會,趕快 畫遞歸圖 吧
由于遞歸太龐大,圖片太小看不清,所以我把左子樹和右子樹分開又截了圖
1.紅線部分代表壓棧遞歸。
2.綠線部分代表 返回
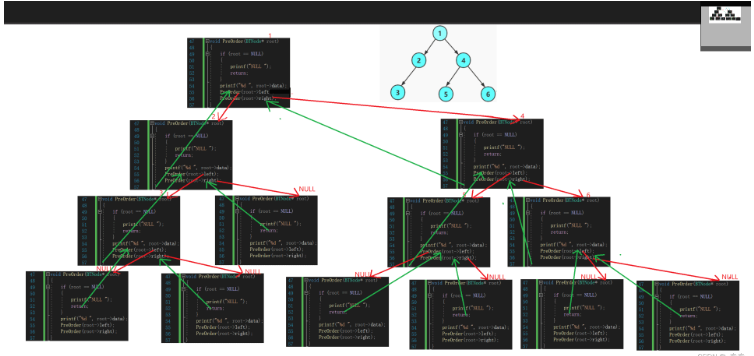
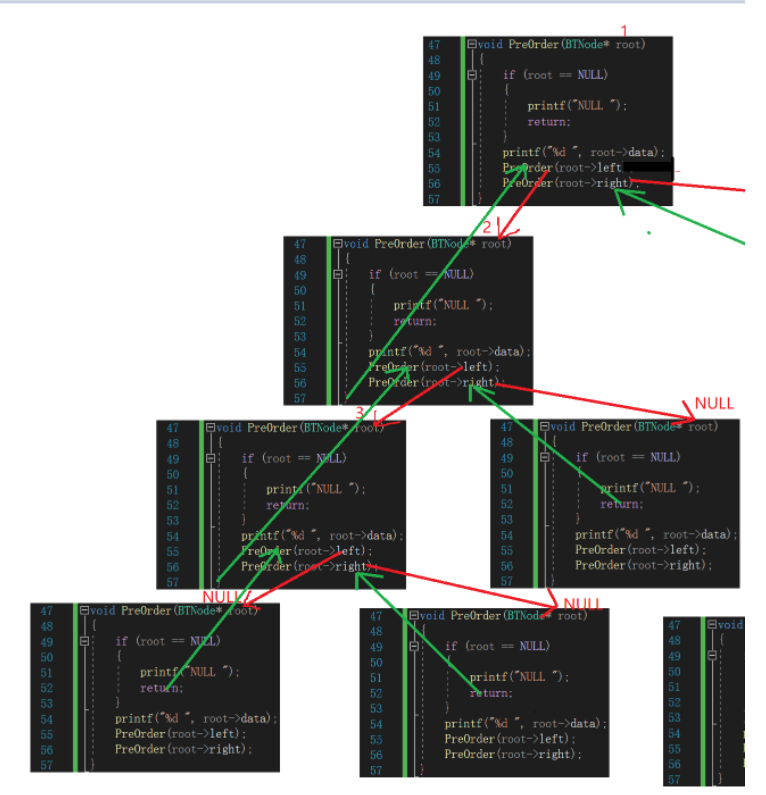
左子樹
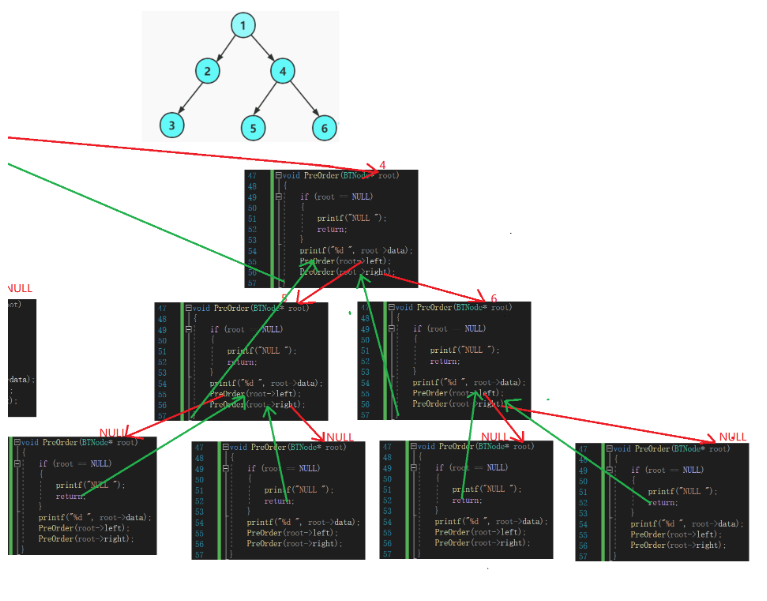
右子樹
遍歷順序:左子樹 根 右子樹
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
//打印在中間
printf("%d ", root->data);
InOrder(root->right);
}打印結果
NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL
遍歷順序:左子樹 右子樹 根
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
//打印在最后
printf("%d ", root->data);
}打印結果
NULL NULL 3 NULL 2 NULL NULL 5 NULL NULL 6 4 1
5.層序遍歷
思路:
借助先進先出的性質,上一層節點出的時候,帶下一層的節點進去。
1.先把根入隊列。
2.根節點出來的時候,左右孩子進去。
// 層序遍歷
void LevelOrder(BTNode* root)
{
//初始化隊列,注意隊列里面存的是 指針類型。
Queue q;
QueueInit(&q);
//如果樹不為空開始入隊
if (root)
{
QueuePush(&q, root);
}
//樹不為空開始出對頭數據,同時入隊左子樹和右子樹,直到隊列為空。
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%d ", front->data);
//如果還有左右子樹,繼續入隊,否則不入隊
if (front->left)
{
QueuePush(&q, front->left);
}
if (front->right)
{
QueuePush(&q, front->right);
}
}
//記得銷毀隊列
printf("\n");
QueueDestory(&q);
}思想:把大問題逐步分割為子問題。
思路:
1.樹為空時返回0個節點。(樹為空不意味著才開始就是空樹,而是遞歸到最后一個為NULL的樹返回)
2.樹不為空時返回自己的1個節點+上一顆樹返回的節點的個數。
// 二叉樹節點個數
int BinaryTreeSize(BTNode* root)
{
//當樹為空時
if (root == NULL)
return 0;
//當樹不為空時
return BinaryTreeSize(root->left) +
BinaryTreeSize(root->right) + 1;
}2.求葉子節點個數
思路:
1.樹為NULL時,返回0.
2.兩顆子樹都不為NULL時,返回1.
3.不滿足以上兩種情況,繼續遞歸左右子樹。
// 二叉樹葉子節點個數
int BinaryTreeLeafSize(BTNode* root)
{
//當樹為空時
if (root == NULL)
return 0;
//當兩棵 子 樹都為空時
if (root->left == NULL && root->right == NULL)
return 1;
/*程序都到這一行, 意味著樹不滿足返回的情況,
所以繼續遞歸 左子樹和 右子樹。*/
return BinaryTreeLeafSize(root->left)+
BinaryTreeLeafSize(root->right);
}
思想:求上圖第3層節點個數。
1.站在第1層來看,就是求第3層節點的個數
2.站在第2層的角度來看,就是求第2層節點的個數
3.站在第3層的角度來看,就是求第1層節點的個數
思路:
1.當樹為空時返回0
2.當k為1時返回1。
3.不滿足1和2,繼續遞歸左右子樹。
// 二叉樹第k層節點個數
int BinaryTreeLevelKSize(BTNode* root, int k)
{
//當樹為空時
if (root == NULL)
return 0;
//當k為1時
if (k == 1)
return 1;
//程序能走到這一行,說明樹不為空,k也不為1.繼續遞歸
return BinaryTreeLevelKSize(root->left, k-1)+
BinaryTreeLevelKSize(root->right, k - 1);
}思想:
1.把最小規模的問題寫在最前面作為限制
2.不滿足最小規模的問題,則繼續遞歸。將問題一步一步拆分為不可分割的子問題。
// 二叉樹查找值為x的節點
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
//當樹為空時
if (root == NULL)
return NULL;
//當樹的值等于x時
if (root->data == x)
return root;
/*走到這一行,說明不滿足以上條件。
開始遞歸左右子樹,如果找到了,直接一步一步往回返*/
BTNode* a = BinaryTreeFind(root->left, x);
if (a)
{
return a;
}
BTNode* b = BinaryTreeFind(root->right, x);
if (b)
{
return b;
}
//沒有x,則返回空
return NULL;
}思路:相當于二叉樹的后序遍歷。
先把左右子樹遍歷完后,開始遍歷根,對根進行free。
// 二叉樹銷毀
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
return;
BinaryTreeDestory(root->left);
BinaryTreeDestory(root->right);
//free掉根
free(root);
}思路:
對一串字符進行先序遍歷,遞歸遍歷二叉樹,當遇見#時開始返回 連接 樹。
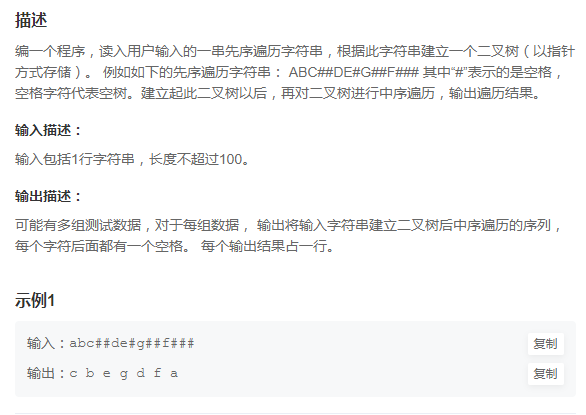
通過前序遍歷的數組"ABD##E#H##CF##G##"構建二叉樹
#include <stdio.h>
#include <stdlib.h>
typedef struct BTNodeTree
{
struct BTNodeTree* left;
struct BTNodeTree* right;
char val;
}BTNode;
//創建二叉樹
BTNode* CreateTree(char* a, int* pi)
{
//如果樹為#則返回null
if(a[*pi] == '#')
{
(*pi)++;
return NULL;
}
//否則構建節點,同時讓pi++,以便繼續遞歸
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
root->val = a[(*pi)++];
//構建左右子樹
root->left = CreateTree(a, pi);
root->right = CreateTree(a, pi);
//構建完后返回根節點。
return root;
}
//中序遍歷打印。
void inorder(BTNode* root)
{
if(root == NULL)
return;
inorder(root->left);
printf("%c ", root->val);
inorder(root->right);
}
int main()
{
char a[100];
scanf("%s", a);
int i = 0;
BTNode* tree = CreateTree(a, &i);
inorder(tree);
return 0;
}思路:
1.層序遍歷,空節點也進隊列
2.出到空節點以后,出隊列中所有數據,如果全是空,則是完全二叉樹
思路:二叉樹的最大深度等價于:左右子樹的最大深度 + 1
int maxDepth(struct TreeNode* root)
{
if(root == NULL)
{
return 0;
}
size_t left = maxDepth(root->left) + 1;
size_t right = maxDepth(root->right) + 1;
if(right > left)
{
return right;
}
return left;
}//判斷二叉樹是否是完全二叉樹
bool BTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
break;
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
//空后面出到非空,那說明不是完全二叉樹
if (front)
return false;
}
//否則是完全二叉樹
return true;
}以下題目均屬于LeetCode的 簡單 題目

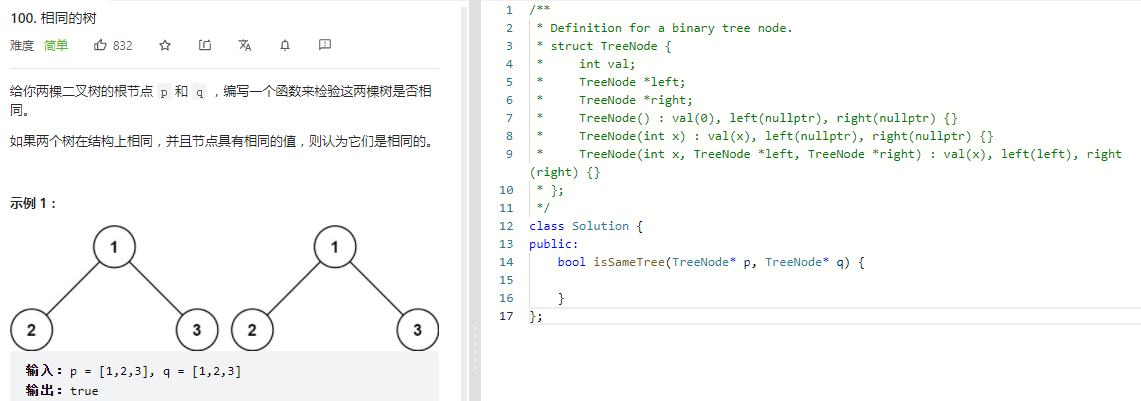
如果二叉樹每個節點都具有相同的值,那么該二叉樹就是單值二叉樹。
只有給定的樹是單值二叉樹時,才返回 true;否則返回 false。
思想:
1.看一棵樹的三個部分是否相同,相同則繼續遞歸下一顆樹,直到樹為空。
bool isUnivalTree(struct TreeNode* root)
{
//當樹為空時。
if(root == NULL)
{
return true;
}
//當右樹不為空,并且 根 != 左樹
//當右樹不為空,并且 根 != 右樹時
if(root->left != NULL && root->val != root->left->val)
return false;
if(root->right != NULL && root->val != root->right->val)
return false;
//能走到這一行,說明第一層樹的值相同了。接著遞歸左右子樹。
return isUnivalTree(root->left) &&
isUnivalTree(root->right);
}
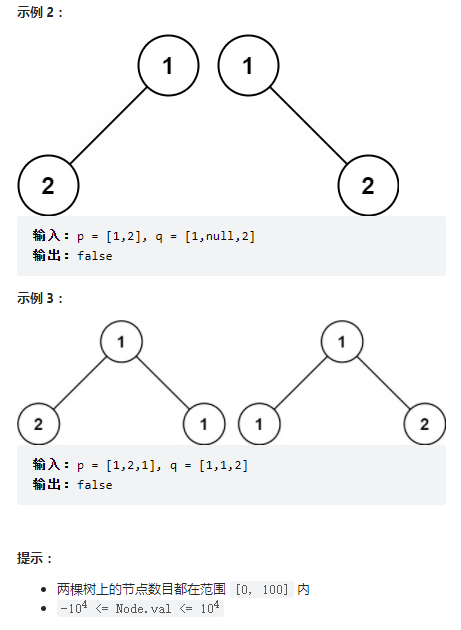
給你兩棵二叉樹的根節點 p 和 q ,編寫一個函數來檢驗這兩棵樹是否相同。
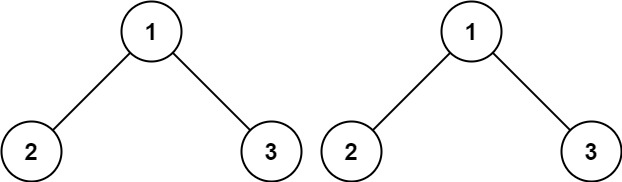
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
//當兩樹都為空時
if(p == NULL && q== NULL)
return true;
//當其中一個樹為空時
if(p == NULL || q == NULL)
return false;
//走到這里說明兩樹存在,比較兩樹的值
if(p->val != q->val)
return false;
//走到這里說明兩樹的根節點相同,繼續遞歸,直到判斷完左右子樹為止。
return isSameTree(p->left, q->left)
&& isSameTree(p->right, q->right);
}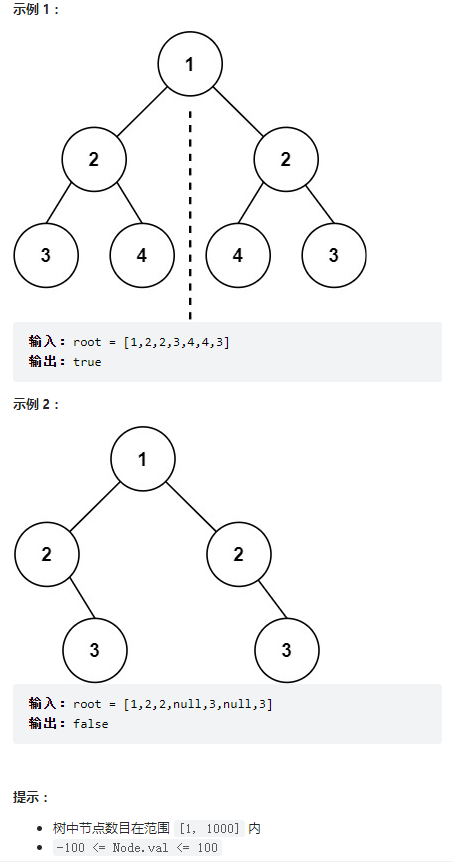
給你一個二叉樹的根節點 root , 檢查它是否軸對稱。
bool isSym(struct TreeNode* q, struct TreeNode* p)
{
//當只有一個根節點時
if(q == NULL && p == NULL)
return true;
//當其中一個子樹為空時
if(q == NULL ||p ==NULL)
return false;
//程序走到一這行,說明左右節點存在。當兩個根節點不相等時
if(q->val != p->val)
return false;
//走到這一步說明左右節點相同,開始遞歸左右子樹
return isSym(q->left, p->right) && isSym(q->right, p->left);
}
bool isSymmetric(struct TreeNode* root)
{
//當是空樹時
if(root == NULL)
return true;
return isSym(root->left, root->right);
}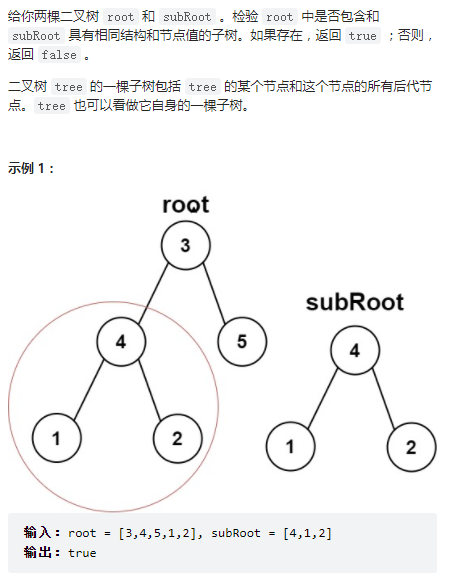
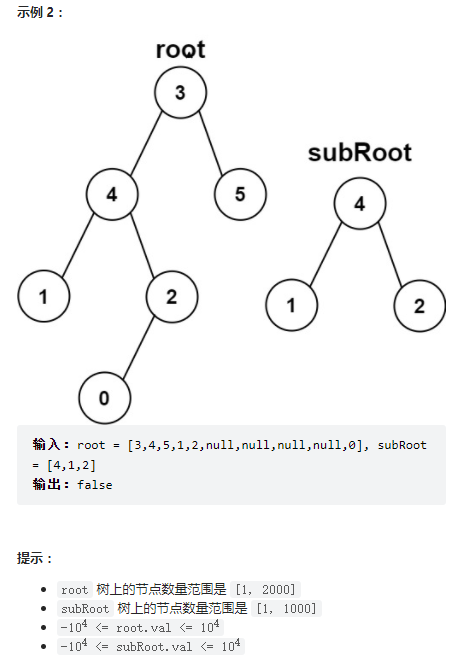
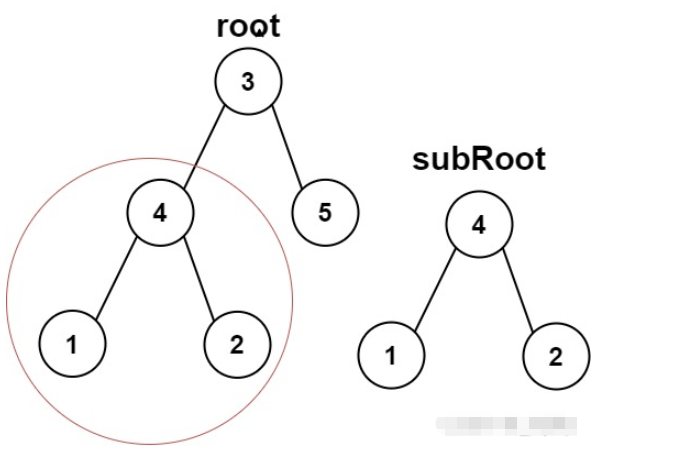
思路:
用到了上一題判斷兩棵樹是否相同的思想。
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
//當兩樹都為空時
if(p == NULL && q== NULL)
return true;
//當其中一個樹為空時
if(p == NULL || q == NULL)
return false;
//走到這里說明兩樹存在,比較兩樹的值
if(p->val != q->val)
return false;
//走到這里說明兩樹的根節點相同,繼續遞歸
return isSameTree(p->left, q->left)
&& isSameTree(p->right, q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
//遞歸結束條件。當根為空時,并不是說明沒有節點,可能是所有的子樹都遍歷過了。然后不相等返回false
if(root == NULL)
return false;
//走到這里說明子樹不為空,開始比較子樹和sub相同不。
bool a = isSameTree(root, subRoot);
if(a)
return a;
//走到這里說明不相同,繼續遞歸左子樹和右子樹,其中一個相同就返回true。
return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}5.二叉樹的前序遍歷
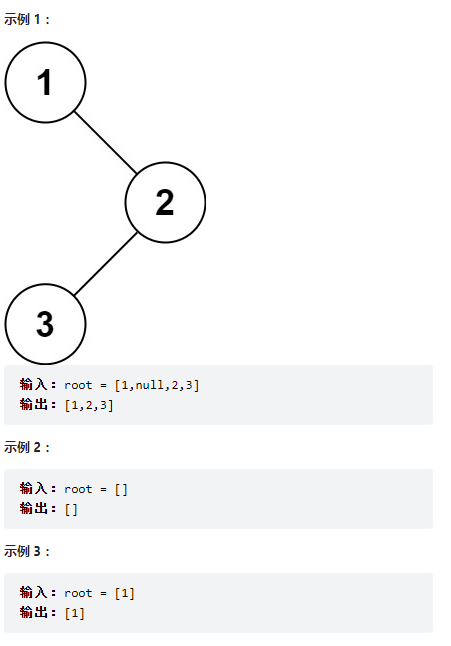
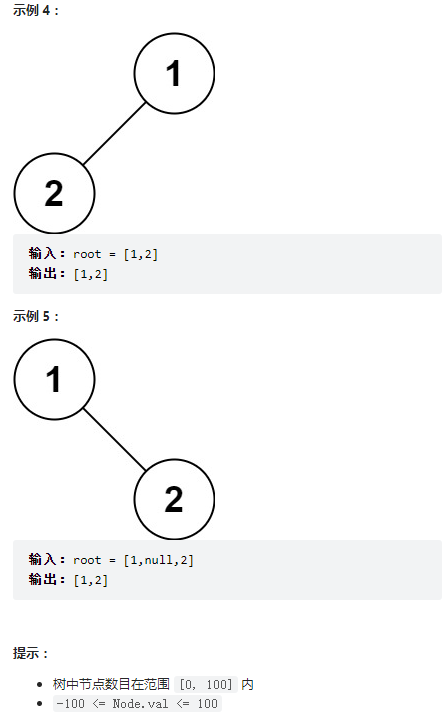
題目思路
1.求節點個數,開辟數組大小。
2.前序遍歷存放到數組中
int treeSize(struct TreeNode* root)
{
if(root == NULL)
return 0;
return treeSize(root->left) + treeSize(root->right)+1;
}
void preorder(int* a, struct TreeNode* root, int* i)
{
if(root == NULL)
{
return;
}
a[(*i)++] = root->val;
preorder(a,root->left, i);
preorder(a,root->right, i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
//計算樹有幾個節點,然后開辟相應的空間
int size = treeSize(root);
int* a = (int*)malloc(sizeof(int)* size);
int i = 0;//設置下標i
*returnSize = size;//需要返回的數組大小
//前序遍歷依次存放到數組中。
preorder(a, root, &i);
return a;
}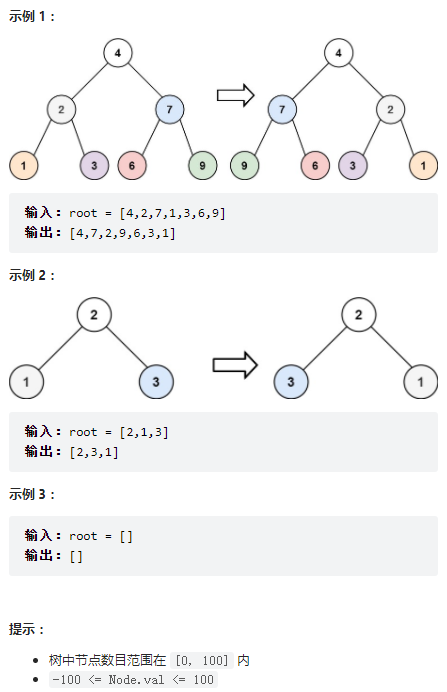
給你一棵二叉樹的根節點 root ,翻轉這棵二叉樹,并返回其根節點。
我犯的BUG:只是對二叉樹里面的值進行交換,但是無法避免空指針。一直都是空指針的錯誤,因為root總會為空,root->data總會遇見空指針
所以以后盡量要多想著交換地址。
void _invertTree(struct TreeNode* root)
{
if(root)
{
struct TreeNode* tmp = root->left;
root->left = root->right;
root->right = tmp;
_invertTree(root->left);
_invertTree(root->right);
}
}
struct TreeNode* invertTree(struct TreeNode* root)
{
_invertTree(root);
return root;
}“C語言數據結構二叉樹遞歸的方法”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。