您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容主要講解“C語言數據結構與算法中枚舉、模擬及排序的方法”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“C語言數據結構與算法中枚舉、模擬及排序的方法”吧!
來源:第四屆藍橋杯省賽C++B組,第四屆藍橋杯省賽JAVAB組
小明這些天一直在思考這樣一個奇怪而有趣的問題:
在 1∼N 的某個排列中有多少個連號區間呢?
這里所說的連號區間的定義是:
如果區間 [L,R] 里的所有元素(即此排列的第 L 個到第 R 個元素)遞增排序后能得到一個長度為 R−L+1 的“連續”數列,則稱這個區間連號區間。
當 N 很小的時候,小明可以很快地算出答案,但是當 N 變大的時候,問題就不是那么簡單了,現在小明需要你的幫助。
輸入格式
第一行是一個正整數 N,表示排列的規模。
第二行是 N 個不同的數字 Pi,表示這 N 個數字的某一排列。
輸出格式
輸出一個整數,表示不同連號區間的數目。
數據范圍
1≤N≤10000,
1≤Pi≤N
輸入樣例1:
4
3 2 4 1
輸出樣例1:
7
輸入樣例2:
5
3 4 2 5 1
輸出樣例2:
9
樣例解釋
第一個用例中,有 7 個連號區間分別是:[1,1],[1,2],[1,3],[1,4],[2,2],[3,3],[4,4]
第二個用例中,有 9 個連號區間分別是:[1,1],[1,2],[1,3],[1,4],[1,5],[2,2],[3,3],[4,4],[5,5]
先來看暴力做法
先兩次for()循環,對給出的數排序,然后再對區間內的數做判斷,如果連續的就res++。
#include <bits/stdc++.h>
using namespace std;
const int N=10010;
int a[N],bac[N];
int main()
{
int n,res=0;
cin >> n;
for(int i=1;i<=n;i++) cin >> a[i];
for(int i=1;i<=n;i++)
for(int j=i;j<=n;j++){
memcpy(bac,a,sizeof a); // 這里要把數組的初始狀態存在bac數組中,因為每次sort排序后,數組的順序會發生改變。
sort(a+i,a+j+1);
bool flag=true;
for(int k=i;k<j;k++){
if(a[k+1] - a[k] != 1){
flag=false;
break;
}
}
if(flag) res++;
memcpy(a,bac,sizeof a); // 還原數組a的初始狀態
}
cout << res << endl;
return 0;
}但是這道題暴力做法在藍橋杯中只能得60分,然后我們再來想一下怎么優化?
這里設兩層循環,一層i表示左端點,第二層j表示右端點。如果要保持連續性的話那么有一個思路:因為是連續的所以在所取的[l,r]范圍中尋找最大值,最小值。然后相減,最后和r-l(區間長度)作比較即可。除此之外當l=r時也算作連續
即MAX-MIN==R-L
#include <bits/stdc++.h>
using namespace std;
const int N = 10010, INF = 100000000;
int n;
int a[N];
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ ) cin >> a[i];
int res = 0;
for (int i = 0; i < n; i ++ ) // 枚舉區間左端點
{
int minv = INF, maxv = -INF;
for (int j = i; j < n; j ++ ) // 枚舉區間右端點
{
minv = min(minv, a[j]);
maxv = max(maxv, a[j]);
if (maxv - minv == j - i) res ++ ;
}
}
cout << res << endl;
return 0;
}來源:第九屆藍橋杯省賽C++B組,第九屆藍橋杯省賽JAVAB組
給定三個整數數組
A=[A1,A2,…AN],
B=[B1,B2,…BN],
C=[C1,C2,…CN],
請你統計有多少個三元組 (i,j,k) 滿足:
1≤i,j,k≤N
Ai<Bj<Ck
輸入格式
第一行包含一個整數 N。
第二行包含 N 個整數 A1,A2,…AN。
第三行包含 N 個整數 B1,B2,…BN。
第四行包含 N 個整數 C1,C2,…CN。
輸出格式
一個整數表示答案。
數據范圍
1≤N≤105,
0≤Ai,Bi,Ci≤105
輸入樣例:
3
1 1 1
2 2 2
3 3 3
輸出樣例:
27
首先考慮暴力做法,三個數組嵌套枚舉,O(n3)的時間復雜度,n≤105一定會超時,這里提供代碼,想試一下的可以試試
//暴力做法枚舉(會超時)
#include <bits/stdc++.h>
using namespace std;
const int N=10000;
int n,a[N],b[N],c[N];
int cnt=0;
int main(){
//輸入
cin>>n;
for(int i=0;i<n;i++) cin>>a[i];
for(int i=0;i<n;i++) cin>>b[i];
for(int i=0;i<n;i++) cin>>c[i];
//運算
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
for(int k=0;k<n;k++)
if(a[i]<b[j]&&b[j]<c[k])
cnt++;
cout<<cnt<<endl;
return 0;
}嘗試通過枚舉的次序進行優化本題,先枚舉B數組,在A中尋找小于B[i]的數的個數cnt1,在C中尋找大于B[i]的數的個數cnt2,帶有B[i]的合法選擇數就是cnt1*cnt2。
用暴力查找時間總的時間復雜度為O(n2),還是會超時。
既然是查找,那么可以考慮進行二分查找,查找前先通過排序預處理三個數組,排序時間復雜度O(nlog2n)O(nlog2n),枚舉B的所有元素+查找A,C中的元素時間復雜度也是O(nlog2n)O(nlog2n),總的時間復雜度降為O(nlog2n)
//二分查找
#include <bits/stdc++.h>
using namespace std;
const int N=100000+6;
int n,a[N],b[N],c[N];
long long res=0;
int main(){
cin>>n;//輸入
for(int i=0;i<n;i++) cin>>a[i];
for(int i=0;i<n;i++) cin>>b[i];
for(int i=0;i<n;i++) cin>>c[i];
//排序
sort(a,a+n);sort(b,b+n);sort(c,c+n);
//查找
for(int i=0;i<n;i++)
{
int low_a=0,right_a=n-1;
while(low_a<right_a) //找比b[i]小的最后一個數
{
int mid=(low_a+right_a+1)>>1;//加1之后改為向上取整
if(a[mid]<b[i]) low_a=mid;
else right_a=mid-1;
}
if(a[low_a]>=b[i]) low_a=-1;//所有數都大于等于b[i]的時候,low_a=-1,這樣最后(low_a+1)*(n-low_b)的時候為0
int low_b=0,right_b=n-1;
while(low_b<right_b) //找比b[i]大的第一個數
{
int mid =(low_b+right_b)>>1;
if(c[mid]>b[i]) right_b=mid;
else low_b=mid+1;
}
if(c[low_b]<=b[i]) low_b=n;//所有數都小于等于b[i]的時候,low_b=n,這樣最后(low_a+1)*(n-low_b)的時候為0
//if(low_a!=0&&low_b!=n-1)//最開始的時候用這種方法判斷,后來發現不行
//如果只有一個數字可以的時候,這種情況無法判斷,
// 例如:
// 1 4 5
// 5 5 9
// 4 6 7(10) 當b[i]=9的時候,c[i]=7和10的時候無法判斷
res+=(long long)(low_a+1)*(n-low_b);
}
cout<<res<<endl;
return 0;
}進一步對查找進行優化,對于排過序的數組A和B,尋找A中小于B[i]的元素的個數可以考慮雙指針算法,因為每個指針最多移動n次,故查找的時間復雜度降到O(n),查找C與查找A同理,只是找第一個大于B的位置。
只需要將上述二分程序中的
//二分
for(int i = 1; i <= n; ++i) {
int key = num[1][i];
//A中二分查找第一個小于key的數的下標
int pos1 = lower_bound(num[0]+1, num[0]+n+1, key)-num[0]-1;
//C中二分查找第一個大于key的數的下標
int pos2 = upper_bound(num[2]+1, num[2]+n+1, key)-num[2];
if(pos1 >= 1 && pos2 <= n) {
ans += (LL)pos1*(n-pos2+1);
}
}更改為
//雙指針
int a = 1, c = 1;
for(int i = 1; i <= n; ++i) {
int key = num[1][i];
while(a<=n && num[0][a] < key) a++;
while(c<=n && num[2][c] <= key) c++;
ans += (LL)(a-1)*(n-c+1);
}完整的雙指針程序為:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5+10;
int num[3][N];
int main() {
int n;
scanf("%d", &n);
for(int i = 0; i < 3; ++i)
for(int j = 1; j <= n; ++j)
scanf("%d", &num[i][j]);
for(int i = 0; i < 3; ++i)
sort(num[i]+1, num[i]+n+1);
LL ans = 0;
//枚舉B,尋找A滿足的個數以及C滿足的個數相乘
int a = 1, c = 1;
for(int i = 1; i <= n; ++i) {
int key = num[1][i];
while(a<=n && num[0][a] < key) a++;
while(c<=n && num[2][c] <= key) c++;
ans += (LL)(a-1)*(n-c+1);
}
cout<<ans<<endl;
return 0;
}之前的雙指針算法時間復雜度的瓶頸為:排序O(nlog2n)O(nlog2n)
考慮是否可以不排序在O(n)的時間內解決此問題呢?
既然要排序實現快速的查找A中小于B[i]的數的個數,可以將數組A中所有元素出現的次數存入一個哈希表中,因為數組中元素的范圍只有n5n5, 可以開一個大的數組cnta 作為哈希表。
在枚舉B中元素時,我們需要快速查找找小于B[i]的所有元素的總數,只需要在枚舉之前先將求出表中各數的前綴和即可。
查找C與查找A同理可得。
//前綴和
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5+10;
int A[N], B[N], C[N];
int cnta[N], cntc[N], sa[N], sc[N];
int main() {
int n;
scanf("%d", &n);
//獲取數i在A中有cntc[i]個,并對cnt求前綴和sa
for(int i = 1; i <= n; ++i) {
scanf("%d", &A[i]);
cnta[++A[i]]++;
}
sa[0] = cnta[0];
for(int i = 1; i < N; ++i) sa[i] = sa[i-1]+cnta[i];
//B只讀取即可
for(int i = 1; i <= n; ++i) scanf("%d", &B[i]), B[i]++;
//獲取數i在C中有cntc[i]個,并對cnt求前綴和sc
for(int i = 1; i <= n; ++i) {
scanf("%d", &C[i]);
cntc[++C[i]]++;
}
sc[0] = cntc[0];
for(int i = 1; i < N; ++i) sc[i] = sc[i-1]+cntc[i];
//遍歷B求解
LL ans = 0;
for(int i = 1; i <= n; ++i) {
int b = B[i];
ans += (LL)sa[b-1] * (sc[N-1] - sc[b]);
}
cout<<ans<<endl;
return 0;
}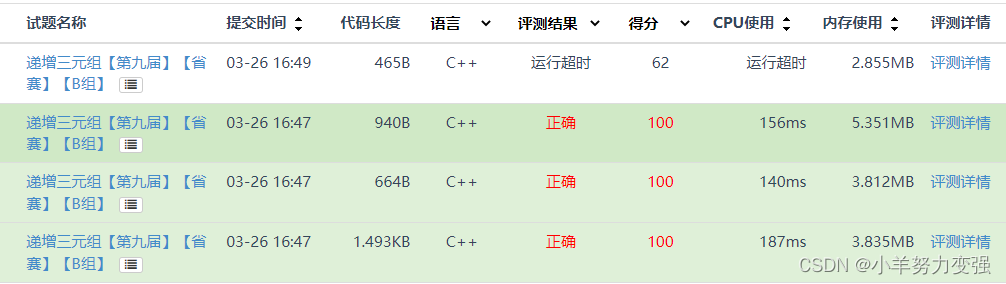
分別是暴力,前綴和,雙指針,二分。
來源:第十屆藍橋杯省賽C++B組,第十屆藍橋杯省賽JAVAB組
小明對數位中含有 2、0、1、9 的數字很感興趣(不包括前導 0),在 1 到 40 中這樣的數包括 1、2、9、10 至 32、39 和 40,共 28 個,他們的和是 574。
請問,在 1 到 n 中,所有這樣的數的和是多少?
輸入格式
共一行,包含一個整數 n。
輸出格式
共一行,包含一個整數,表示滿足條件的數的和。
數據范圍
1≤n≤10000
輸入樣例:
40
輸出樣例:
574
常用小技巧:關于取出x的每位數字 和 將字符數字轉為數字
1.取出x的每位數字
int t = x % 10;
x /= 10;
2.將字符數字轉為數字
int x = 0;
for (int i = 0; i < str.size(); i ++ )
x = x * 10 + str[i] - '0';
下面請看你代碼:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin >> n;
int res = 0;
for (int i = 1; i <= n; i ++ )
{
int x = i;
while (x)
{
int t = x % 10; // 取出x的個位
x /= 10; // 刪掉x的個位
if (t == 2 || t == 0 || t == 1 || t == 9)
{
res += i;
break;
}
}
}
cout << res << endl;
return 0;
}來源:第四屆藍橋杯省賽C++A/B組,第四屆藍橋杯省賽JAVAA/B組
某涉密單位下發了某種票據,并要在年終全部收回。
每張票據有唯一的ID號。
全年所有票據的ID號是連續的,但ID的開始數碼是隨機選定的。
因為工作人員疏忽,在錄入ID號的時候發生了一處錯誤,造成了某個ID斷號,另外一個ID重號。
你的任務是通過編程,找出斷號的ID和重號的ID。
假設斷號不可能發生在最大和最小號。
輸入格式
第一行包含整數 N,表示后面共有 N 行數據。
接下來 N 行,每行包含空格分開的若干個(不大于100個)正整數(不大于100000),每個整數代表一個ID號。
輸出格式
要求程序輸出1行,含兩個整數 m,n,用空格分隔。
其中,m表示斷號ID,n表示重號ID。
數據范圍
1≤N≤100
輸入樣例:
2
5 6 8 11 9
10 12 9
輸出樣例:
7 9
思路
找出最大和最小的數,同時再用一個數組記錄每個數字的個數,最后遍歷一遍即可
#include <bits/stdc++.h>
using namespace std;
const int N = 10010;
int n;
int a[N];
int main()
{
int cnt;
cin >> cnt;
string line;
getline(cin, line); // 忽略掉第一行的回車
while (cnt -- )
{
getline(cin, line);
stringstream ssin(line);
while (ssin >> a[n]) n ++ ;
}
sort(a, a + n);
int res1, res2;
for (int i = 1; i < n; i ++ )
if (a[i] == a[i - 1]) res2 = a[i]; // 重號
else if (a[i] >= a[i - 1] + 2) res1 = a[i] - 1; // 斷號
cout << res1 << ' ' << res2 << endl;
return 0;
}給定你一個長度為 n 的整數數列。
請你使用快速排序對這個數列按照從小到大進行排序。
并將排好序的數列按順序輸出。
輸入格式
輸入共兩行,第一行包含整數 n。
第二行包含 n 個整數(所有整數均在 1∼109 范圍內),表示整個數列。
輸出格式
輸出共一行,包含 n 個整數,表示排好序的數列。
數據范圍
1≤n≤100000
輸入樣例:
5
3 1 2 4 5
輸出樣例:
1 2 3 4 5
快排思路
1.有數組 q, 左端點 l, 右端點r
2.確定劃分邊界 x
3.將 q 分為 <=x 和 >=x 的兩個小數組
i 的含義: i 之前的元素都 ≤x, 即 q[l..i−1]q[l..i−1] ≤x
j 的含義: j 之后的元素都 ≥x, 即 q[j+1..r]q[j+1..r] ≥x
結論: while循環結束后, q[l..j] ≤x,q[j+1..r] ≥x
簡單不嚴謹證明:
while 循環結束時, i≥j
若 i>j , 顯然成立
若 i=ji=j
∵∵ 最后一輪循環中兩個 do−whiledo−while 循環條件都不成立
∴ q[i]≥x,q[j]≤x
∴ q[i]=q[j]=x
∴ 結論成立
4.遞歸處理兩個小數組
#include <iostream>
using namespace std;
const int N = 100010;
int q[N];
void quick_sort(int q[], int l, int r)
{
if (l >= r) return;
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while (i < j)
{
do i ++ ; while (q[i] < x);
do j -- ; while (q[j] > x);
if (i < j) swap(q[i], q[j]);
}
quick_sort(q, l, j);
quick_sort(q, j + 1, r);
}
int main()
{
int n;
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);
quick_sort(q, 0, n - 1);
for (int i = 0; i < n; i ++ ) printf("%d ", q[i]);
return 0;
}歸并的題和快排的題是一樣的,這里就不寫題目了。
歸并思路
1.有數組 q, 左端點 l, 右端點 r
2.確定劃分邊界 mid
3.遞歸處理子問題 q[l..mid], q[mid+1..r]
4.合并子問題
主體合并
至少有一個小數組添加到 tmp 數組中
收尾
可能存在的剩下的一個小數組的尾部直接添加到 tmp 數組中
復制回來
tmp 數組覆蓋原數組
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N], tmp[N];
void merge_sort(int q[], int l, int r)
{
if (l >= r) return;
int mid = l + r >> 1;
merge_sort(q, l, mid), merge_sort(q, mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
else tmp[k ++ ] = q[j ++ ];
while (i <= mid) tmp[k ++ ] = q[i ++ ];
while (j <= r) tmp[k ++ ] = q[j ++ ];
for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}
int main()
{
int n;
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
merge_sort(a, 0, n - 1);
for (int i = 0; i < n; i ++ ) printf("%d ", a[i]);
return 0;
}到此,相信大家對“C語言數據結構與算法中枚舉、模擬及排序的方法”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。