python中leastsq函數如何使用

本篇內容介紹了“python中leastsq函數如何使用”的有關知識，在實際案例的操作過程中，不少人都會遇到這樣的困境，接下來就讓小編帶領大家學習一下如何處理這些情況吧！希望大家仔細閱讀，能夠學有所成！

leastsq作用：最小化一組方程的平方和。

參數設置：

• func 誤差函數

• x0 初始化的參數

• args 其他的額外參數

舉個例子：

首先創建樣本點

import numpy as np
import scipy as sp
from scipy.optimize import leastsq
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
x=[1,2,3,4]
y=[2,3,4,5]

擬合直線

def y_pre(p,x):
    f=np.poly1d(p)
    return f(x)

其中的np.polyld

f=np.poly1d([1,2,3])
 # x^2+2x+3
f(1)
"""
6
"""

誤差函數

def error(p,x,y):
    return y-y_pre(p,x)

接下就簡單了

p=[1,2]    # 值隨便寫
# y=w1*x+w2
res=leastsq(error,p,args=(x,y))
w1,w2=res[0]   # res[0]中就是wi的參數列表
"""
到這w1和w2就已經求出來了，下面是畫圖看一下
"""
x_=np.linspace(1,10,100)   # 等差數列，
y_p=w1*x_+w2               # 求出的擬合曲線
plt.scatter(x,y)           # 樣本點
plt.plot(x_,y_p)           # 畫擬合曲線

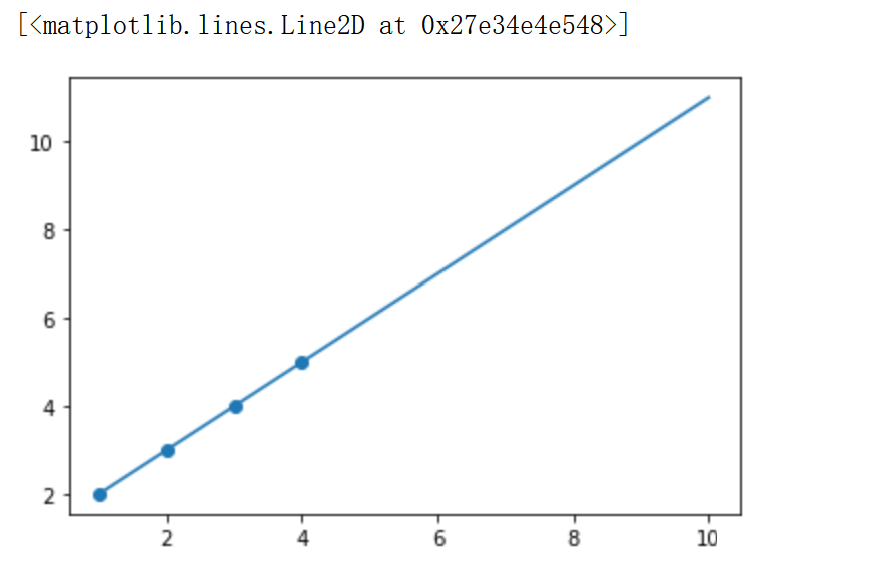
可以直接封裝成函數

x=np.linspace(0,2,10)
y=np.sin(np.pi*x)
# 原始的樣本
y_=[y + np.random.normal(0,0.1) for y in y]     # np.random.normal(loc,scale,size):正態分布的均值,正態分布的標準差,形狀

# np.random.randn()   # 標準正態分布是以0為均數、以1為標準差的正態分布，記為N（0，1）

def fit(M=1):
    p=np.random.rand(M+1)   # 返回一個或一組服從“0~1”均勻分布的隨機樣本值。隨機樣本取值范圍是[0,1)
    res=leastsq(error,p,args=(x,y))  # wi 的值
    x_point=np.linspace(0,2,100)  # 增加數據量為了畫出的圖平滑
    y_point=np.sin(np.pi*x_point) # 增加數據量為了畫出的圖平滑
    plt.plot(x_point,y_point,'r',label='原始')
    plt.plot(x_point,y_pre(res[0],x_point),'b',label='擬合')
    plt.scatter(x,y_)
    plt.legend()
fit(3)

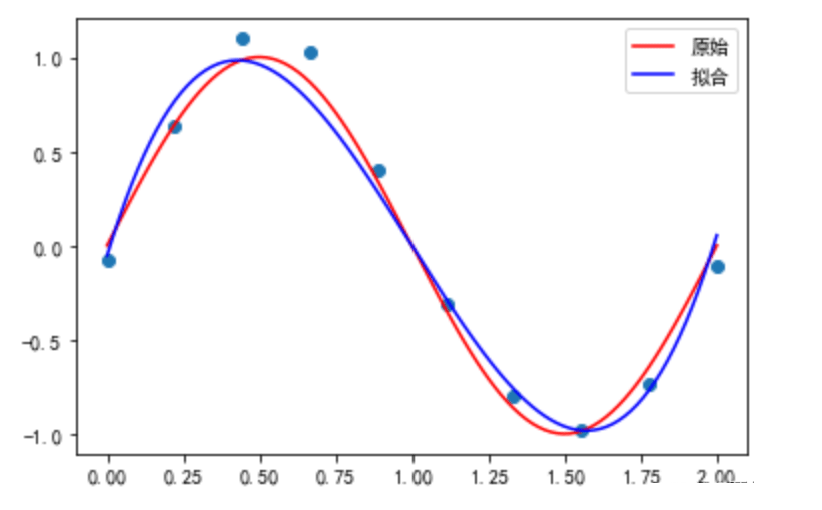
你也可以輸出一下中間的結果：

x=np.linspace(0,2,10)
y=np.sin(np.pi*x)
# 原始的樣本
y_=[y + np.random.normal(0,0.1) for y in y]     # np.random.normal(loc,scale,size):正態分布的均值,正態分布的標準差,形狀

# np.random.randn()   # 標準正態分布是以0為均數、以1為標準差的正態分布，記為N（0，1）

def fit(M=1):
    p=np.random.rand(M+1)   # 返回一個或一組服從“0~1”均勻分布的隨機樣本值。隨機樣本取值范圍是[0,1)
    res=leastsq(error,p,args=(x,y))  # wi 的值
    x_point=np.linspace(0,2,100)
    y_point=np.sin(np.pi*x_point)
    plt.plot(x_point,y_point,'r',label='原始')
    plt.plot(x_point,y_pre(res[0],x_point),'b',label='擬合')
    print(res[0])
    plt.scatter(x,y_)
    plt.legend()
fit(3)

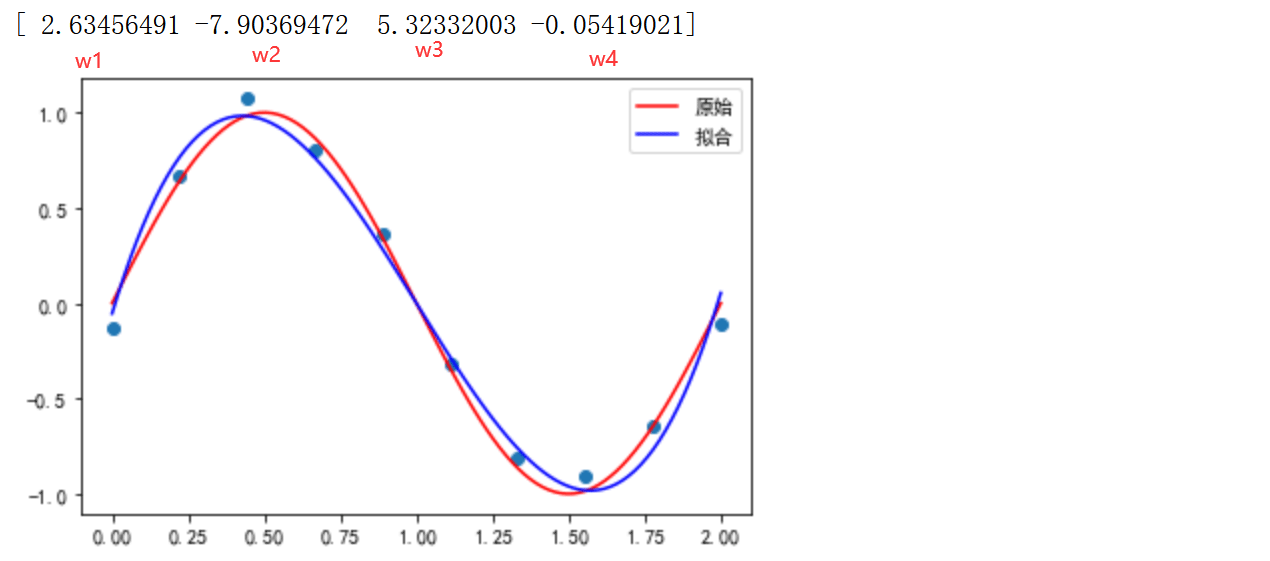
擬合的直線就是：

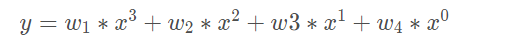
“python中leastsq函數如何使用”的內容就介紹到這里了，感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站，小編將為大家輸出更多高質量的實用文章！