C語言如何求最大公約數

本篇內容介紹了“C語言如何求最大公約數”的有關知識，在實際案例的操作過程中，不少人都會遇到這樣的困境，接下來就讓小編帶領大家學習一下如何處理這些情況吧！希望大家仔細閱讀，能夠學有所成！

1. C語言簡介

1.1 C語言發展史

C語言是一種廣泛使用的面向過程的計算機程序設計語言，既適合于系統程序設計，又適合于應用程序設計。C語言的發展歷程大致如圖1-1所示：

圖1-1 C語言的發展歷程

1.2 C語言的特點

C語言是一種通用的程序設計語言，語言本身簡潔、靈活、表達能力強，被廣泛用于系統軟件和應用軟件的開發，并且具有良好的可移植性。

C語言的特點可概括如下：

（1）簡潔、緊湊、靈活。C語言的核心內容很少，只有32個關鍵字，9種控制語句；程序書寫格式自由，壓縮了一切不必要的成分。

（2）表達方式簡練、實用。C語言有一套強有力的運算符，達44種，可以構造出多種形式的表達式，用一個表達式就可以實現其他語言可能需要多條語句才能實現的功能。

（3）數據類型豐富。數據類型越多，數據的表達能力就越強。C語言具有多種數據類型，如字符型、整型、實型、數組、指針、結構體和共用體等，可以實現諸如鏈表、棧、隊列、樹等各種復雜的數據結構。其中的指針類型使得參數的傳遞簡單并且迅速，同時節省內存空間。

（4）具有低級語言的特點。C語言具有與匯編語言相近的功能和描述方法，如地址運算和二進制數位運算等，還可以對硬件端口等資源進行直接操作，充分使用計算機的資源。C語言既具有高級語言便于學習和掌握的特點，又具有機器語言或匯編語言對硬件的操作能力。因此，C語言既可以作為系統描述語言，又可以作為通用的程序設計語言。

（5）C語言是一種結構化語言，適合于大型程序的模塊化設計。C語言提供了編寫結構化程序的基本控制語句，如if-else語句、switch語句、while語句和do-while語句等。C語言是函數的集合，函數是構成C語言程序的基本單位，每個函數具有獨立的功能，函數之間通過參數傳遞數據。程序員可以編寫自己的函數。同時，不同操作系統的編譯器都為程序員提供了大量的標準庫函數，如輸入/輸出函數、數學函數和字符串處理函數等。靈活地使用標準庫函數可以簡化程序設計，提高編寫程序效率。

（6）各種版本的編譯器都提供了預處理命令和預處理程序。預處理擴展了C語言的功能，提高了程序的可移植性，為大型程序的調試提供了方便。

（7）可移植性好。程序從一個環境不經改動或稍加改動就可以移植到另一個完全不同的環境中運行。這是因為標準庫函數和預處理程序將可能出現的與機器有關的因素與源程序分割開來，使得針對不同的計算機硬件環境，可以重新定義有關的內容。

（8）生成的目標代碼質量高。由C源程序編譯和鏈接得到的目標代碼的運行效率比用匯編語言編寫的也不過只低10%~20%，可充分發揮機器的效率。

（9）C語言語法限制不嚴，程序設計自由度大。C語言程序在運行時不做諸如數組下標越界和變量類型兼容性等檢查，而是由編程者自己保證程序的正確性。C語言幾乎允許所有的數據類型的轉換，字符型和整型可以自由混合使用，所有類型均可作邏輯型，可自己定義新的類型，還可以把某類型強制轉換為指定的類型。實際上，這使編程者有了更大的自主性，能編寫出靈活、優質的程序，同時也給初學者增加了一定的難度。所以，只有在熟練掌握C語言程序設計之后，才能體會到其靈活性。

C語言也存在以下缺點：

（1）程序的錯誤更隱蔽。C語言的靈活性使得用它編寫程序時更容易出錯，而且C的編譯器不檢查這樣的錯誤。與匯編語言類似，需要程序運行時才能發現這些邏輯錯誤。C語言還會有一些隱患，如將比較的 “==” 寫成賦值 “=” ，雖然語法上沒錯，但這樣的邏輯錯誤往往不易發現，想要找出錯誤往往十分費時。

（2）C語言程序有時會難以理解。C語言語法成分相對簡單，是一種小型語言。但是，其數據類型多，運算符豐富且結合性多樣，使得對其理解有一定的難度。

（3）C語言程序有時會難以修改。考慮到程序規模的大型化或者巨型化，現在編程語言通常會提供 “類” 和 “包” 之類的語言特性，這樣的特性可以將程序分解成更加易于管理的模塊。然而C語言缺少這樣的特性，維護大型程序顯得比較困難。

1.3算法及其表示

C語言解題時，在程序中有兩方面的描述，即數據描述和處理步驟（算法）描述，后者處理前者的數據。

算法具有以下特性：

• 有窮性：算法在執行了有限步驟后結束，并且每一步都可以在有窮的時間內完成。      

• 確定性：算法中每種操作必須有確切的含義，即無二義性。同時，無論如何算法只有唯一的一條執行路徑，即相同的輸入只能得出相同的輸出。      

• 可行性：算法中描述的操作都可以通過已經實現的基本操作執行有限次數來實現。      

• 輸入：有零個或多個輸入，即算法需要的必要信息。      

• 輸出：有一個或多個輸出，輸出的是與輸入有某些特定關系的信息。沒有輸出的算法是無意義的。

算法的表示：

1.自然語言描述；    

2.傳統流程圖；    

3.N-S流程圖；    

4.偽代碼。

【例如】求兩個正整數m和n的最大公約數（即同時能夠整除m和n的最大正整數）。

1. 自然語言描述

歐幾里得闡述了求兩個數的最大公約數的過程——歐幾里得算法

第一步：以n除m，并令r為所得余數（顯然n>r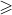0）。

第二步：若r=0,算法結束，n即為m和n的最大公約數。

第三步：置m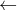n，n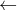r，返回第一步。

2. 傳統流程圖

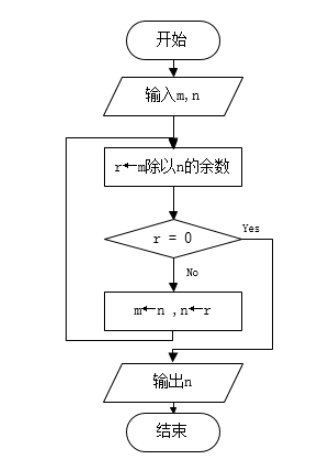
圖1-2 求最大公約數的傳統流程圖

3. N-S流程圖

圖1-3 求最大公約數的N-S流程圖

4. 偽代碼

算法開始
輸入m,n;
do{
    r←以n除m的余數；
    m←n;
    n←r;
}while(r≠0);
輸出m;
算法結束

1.4常用算法介紹

1.枚舉法

枚舉法又稱為窮舉法。該方法通過逐一考察問題的所有可能解，找出問題真正的解。枚舉法要求問題的可能解必須是有限的，而且這些可能解是已知的。

【例】給定一個正整數，確定它的整數立方根是否存在，若存在則找出這個立方根。

算法開始
輸入一個正整數給n;
x←0;
while(x≤n 且 x*x*x≠n){
    x←x+1;
}
if(x≤n)
    找到n的整數立方根，輸出x的值；
else
    輸出n的整數立方根不存在信息；
算法結束

2.遞推法

遞推法是從已知的初始條件出發，逐次推出中間結果。在理想狀態下，每遞推一次，結果逐漸接近問題的最后解。遞推法在數值算法中又稱為迭代法。迭代法常用于求近似解的問題，根據對前一步結果的誤差的不同處理方法，迭代法又有逼近迭代和試探迭代等不同方法。數值計算要注意解的穩定性問題，即在迭代中每一步的解越來越接近真正的解，否則迭代不會成功。

【例】計算一個正整數n的階乘。

算法開始
輸入一個正整數給n；
t←1;
i←1;
while(i≤n){
    t←t*i;
    i←i+1;
}
輸出結果t
算法結束

3.遞歸法

一個直接或間接調用過程（或函數）自身的算法稱為遞歸算法，一個函數如果調用自身進行計算則稱該函數為遞歸函數。一些問題的算法描述中，遞歸法往往比非遞歸法更加簡潔易懂。

【例】計算一個正整數N的階乘。

階乘函數f的遞歸定義為：
f(1)=1                (1!=1,N=1 時)
f(N)=N*f(N-1)         (N!=N*(N-1)!,如果N>1)

除了上面介紹的枚舉法、遞推法和遞歸法外，還有回溯法、貪婪法、分治法、動態規劃法等

“C語言如何求最大公約數”的內容就介紹到這里了，感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站，小編將為大家輸出更多高質量的實用文章！