如何使用Python和Matla實現模擬退火法

這篇文章主要為大家展示了“如何使用Python和Matla實現模擬退火法”，內容簡而易懂，條理清晰，希望能夠幫助大家解決疑惑，下面讓小編帶領大家一起研究并學習一下“如何使用Python和Matla實現模擬退火法”這篇文章吧。

1 Python實現

1.1 源碼實現

我在前面已經給出了模擬退火法的完整知識點和源碼實現：智能優化算法—蟻群算法（Python實現）

模擬退火和蒙特卡洛實驗一樣，全局隨機，由于沒有自適應的過程(例如向最優靠近、權重梯度下降等)，對于復雜函數尋優，很難會找到最優解，都是近似最優解；然而像蝙蝠算法、粒子群算法等有向最優逼近且通過最優最差調整參數的步驟，雖然對于下圖函數易陷入局部最優，但是尋優精度相對較高。如果理解這段話應該就明白了為什么神經網絡訓練前如果初步尋優一組較好的網絡參數，會使訓練效果提高很多，也會更快達到誤差精度。

1.2 sko.SA 實現

#===========1導包================
import matplotlib.pyplot as plt
import pandas as pd
from sko.SA import SA
 
#============2定義問題===============
fun = lambda x: x[0] ** 2 + (x[1] - 0.05) ** 2 + x[2] ** 2
 
#=========3運行模擬退火算法===========
sa = SA(func=fun, x0=[1, 1, 1], T_max=1, T_min=1e-9, L=300, max_stay_counter=150)
best_x, best_y = sa.run()
print('best_x:', best_x, 'best_y', best_y)
 
#=======4畫出結果=======
plt.plot(pd.DataFrame(sa.best_y_history).cummin(axis=0))
plt.show()
 
 
 
 
#scikit-opt 還提供了三種模擬退火流派: Fast, Boltzmann, Cauchy.
 
#===========1.1 Fast Simulated Annealing=====================
from sko.SA import SAFast
 
sa_fast = SAFast(func=demo_func, x0=[1, 1, 1], T_max=1, T_min=1e-9, q=0.99, L=300, max_stay_counter=150)
sa_fast.run()
print('Fast Simulated Annealing: best_x is ', sa_fast.best_x, 'best_y is ', sa_fast.best_y)
 
#===========1.2 Fast Simulated Annealing with bounds=====================
from sko.SA import SAFast
 
sa_fast = SAFast(func=demo_func, x0=[1, 1, 1], T_max=1, T_min=1e-9, q=0.99, L=300, max_stay_counter=150,
                 lb=[-1, 1, -1], ub=[2, 3, 4])
sa_fast.run()
print('Fast Simulated Annealing with bounds: best_x is ', sa_fast.best_x, 'best_y is ', sa_fast.best_y)
 
#===========2.1 Boltzmann Simulated Annealing====================
from sko.SA import SABoltzmann
 
sa_boltzmann = SABoltzmann(func=demo_func, x0=[1, 1, 1], T_max=1, T_min=1e-9, q=0.99, L=300, max_stay_counter=150)
sa_boltzmann.run()
print('Boltzmann Simulated Annealing: best_x is ', sa_boltzmann.best_x, 'best_y is ', sa_fast.best_y)
 
#===========2.2 Boltzmann Simulated Annealing with bounds====================
from sko.SA import SABoltzmann
 
sa_boltzmann = SABoltzmann(func=demo_func, x0=[1, 1, 1], T_max=1, T_min=1e-9, q=0.99, L=300, max_stay_counter=150,
                           lb=-1, ub=[2, 3, 4])
sa_boltzmann.run()
print('Boltzmann Simulated Annealing with bounds: best_x is ', sa_boltzmann.best_x, 'best_y is ', sa_fast.best_y)
 
#==================3.1 Cauchy Simulated Annealing==================
from sko.SA import SACauchy
 
sa_cauchy = SACauchy(func=demo_func, x0=[1, 1, 1], T_max=1, T_min=1e-9, q=0.99, L=300, max_stay_counter=150)
sa_cauchy.run()
print('Cauchy Simulated Annealing: best_x is ', sa_cauchy.best_x, 'best_y is ', sa_cauchy.best_y)
 
#==================3.2 Cauchy Simulated Annealing with bounds==================
from sko.SA import SACauchy
 
sa_cauchy = SACauchy(func=demo_func, x0=[1, 1, 1], T_max=1, T_min=1e-9, q=0.99, L=300, max_stay_counter=150,
                     lb=[-1, 1, -1], ub=[2, 3, 4])
sa_cauchy.run()
print('Cauchy Simulated Annealing with bounds: best_x is ', sa_cauchy.best_x, 'best_y is ', sa_cauchy.best_y)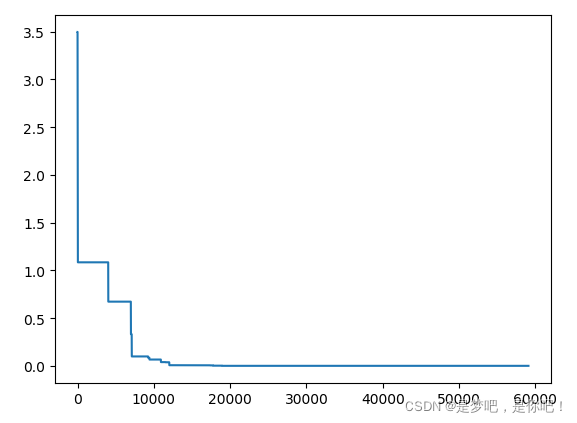

2 Matlab實現 

2.1 模擬退火法

clear
clc
T=1000; %初始化溫度值
T_min=1; %設置溫度下界
alpha=0.99; %溫度的下降率
num=1000; %顆粒總數
n=2; %自變量個數
sub=[-5,-5]; %自變量下限
up=[5,5]; %自變量上限
tu
for i=1:num
for j=1:n
x(i,j)=(up(j)-sub(j))*rand+sub(j);
    end
    fx(i,1)=fun(x(i,1),x(i,2));
end
 
%以最小化為例
[bestf,a]=min(fx);
bestx=x(a,:);
trace(1)=bestf;
while(T>T_min)
for i=1:num
for j=1:n
            xx(i,j)=(up(j)-sub(j))*rand+sub(j);
        end
        ff(i,1)=fun(xx(i,1),xx(i,2));
        delta=ff(i,1)-fx(i,1);
if delta<0
            fx(i,1)=ff(i,1);
x(i,:)=xx(i,:);
else
            P=exp(-delta/T);
if P>rand
                fx(i,1)=ff(i,1);
x(i,:)=xx(i,:);
            end
        end  
    end
if min(fx)<bestf
        [bestf,a]=min(fx);
        bestx=x(a,:);
    end
    trace=[trace;bestf];
    T=T*alpha;
end
disp('最優解為：')
disp(bestx)
disp('最優值為：')
disp(bestf)
hold on
plot3(bestx(1),bestx(2),bestf,'ro','LineWidth',5)
figure
plot(trace)
xlabel('迭代次數')
ylabel('函數值')
title('模擬退火算法')
legend('最優值')

function z=fun(x,y)
z = x.^2 + y.^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20;

function tu
[x,y] = meshgrid(-5:0.1:5,-5:0.1:5);
z = x.^2 + y.^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20;
figure
mesh(x,y,z)%建一個網格圖，該網格圖為三維曲面，有實色邊顏色，無面顏色
hold on
xlabel('x')
ylabel('y')
zlabel('z')
title('z =  x^2 + y^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20')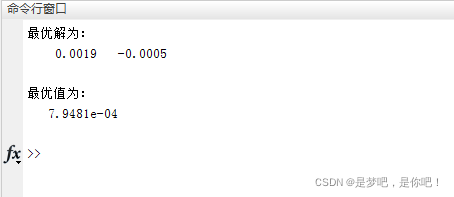

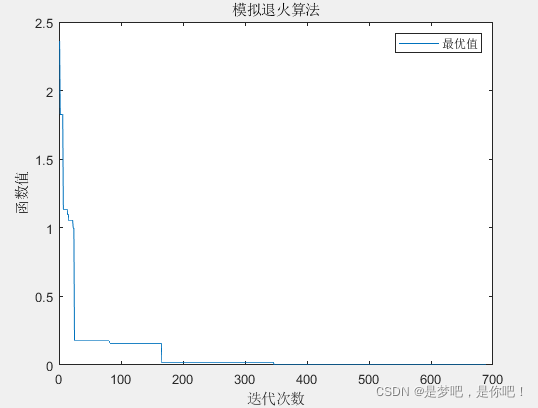
這里有一個待嘗試的想法，先用蒙特卡洛/模擬退火迭代幾次全局去找最優的區域，再通過其他有向最優逼近過程的算法再進一步尋優，或許會很大程度降低產生局部最優解的概率。

下面是模擬退火和蒙特卡洛對上述函數尋優的程序，迭代次數已設為一致，可以思考下兩種程序寫法的效率、共同點、缺點。理論研究講究結果好，實際應用既要保證結果好也要保證程序運算效率。

2.2 蒙特卡諾法 

clear
clc
num=689000; %顆粒總數
n=2; %自變量個數
sub=[-5,-5]; %自變量下限
up=[5,5]; %自變量上限
tu
x=zeros(num,n);
fx=zeros(num,1);
for i=1:num
for j=1:n
x(i,j)=(up(j)-sub(j))*rand+sub(j);
    end
    fx(i,1)=fun(x(i,1),x(i,2));
end
 
[bestf,a]=min(fx);
bestx=x(a,:);
 
disp('最優解為：')
disp(bestx)
disp('最優值為：')
disp(bestf)
hold on
plot3(bestx(1),bestx(2),bestf,'ro','LineWidth',5)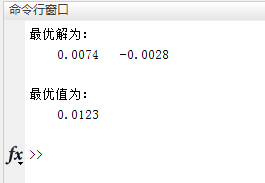

效果確實值得商榷。

以上是“如何使用Python和Matla實現模擬退火法”這篇文章的所有內容，感謝各位的閱讀！相信大家都有了一定的了解，希望分享的內容對大家有所幫助，如果還想學習更多知識，歡迎關注億速云行業資訊頻道！