使用python實現各種插值法的示例

這篇文章將為大家詳細講解有關使用python實現各種插值法的示例，小編覺得挺實用的，因此分享給大家做個參考，希望大家閱讀完這篇文章后可以有所收獲。

一維插值

插值不同于擬合。插值函數經過樣本點，擬合函數一般基于最小二乘法盡量靠近所有樣本點穿過。常見插值方法有拉格朗日插值法、分段插值法、樣條插值法。

• 拉格朗日插值多項式：當節點數n較大時，拉格朗日插值多項式的次數較高，可能出現不一致的收斂情況，而且計算復雜。隨著樣點增加，高次插值會帶來誤差的震動現象稱為龍格現象。

• 分段插值：雖然收斂，但光滑性較差。

• 樣條插值:樣條插值是使用一種名為樣條的特殊分段多項式進行插值的形式。由于樣條插值可以使用低階多項式樣條實現較小的插值誤差，這樣就避免了使用高階多項式所出現的龍格現象，所以樣條插值得到了流行。

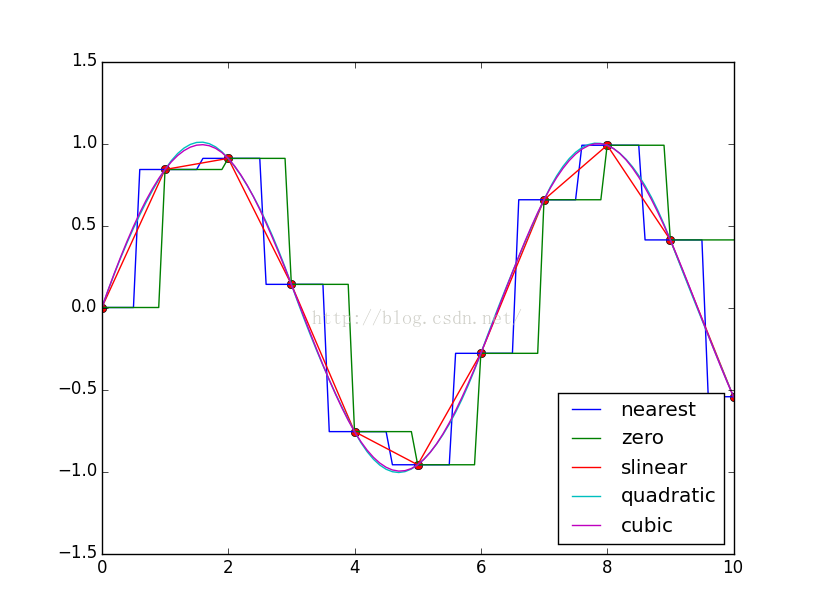
# -*-coding:utf-8 -*-
import numpy as np
from scipy import interpolate
import pylab as pl

x=np.linspace(0,10,11)
#x=[ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.]
y=np.sin(x)
xnew=np.linspace(0,10,101)
pl.plot(x,y,"ro")

for kind in ["nearest","zero","slinear","quadratic","cubic"]:#插值方式
 #"nearest","zero"為階梯插值
 #slinear 線性插值
 #"quadratic","cubic" 為2階、3階B樣條曲線插值
 f=interpolate.interp1d(x,y,kind=kind)
 # ‘slinear', ‘quadratic' and ‘cubic' refer to a spline interpolation of first, second or third order)
 ynew=f(xnew)
 pl.plot(xnew,ynew,label=str(kind))
pl.legend(loc="lower right")
pl.show()

結果：

二維插值

方法與一維數據插值類似，為二維樣條插值。

# -*- coding: utf-8 -*-
"""
演示二維插值。
"""
import numpy as np
from scipy import interpolate
import pylab as pl
import matplotlib as mpl

def func(x, y):
 return (x+y)*np.exp(-5.0*(x**2 + y**2))

# X-Y軸分為15*15的網格
y,x= np.mgrid[-1:1:15j, -1:1:15j]

fvals = func(x,y) # 計算每個網格點上的函數值 15*15的值
print len(fvals[0])

#三次樣條二維插值
newfunc = interpolate.interp2d(x, y, fvals, kind='cubic')

# 計算100*100的網格上的插值
xnew = np.linspace(-1,1,100)#x
ynew = np.linspace(-1,1,100)#y
fnew = newfunc(xnew, ynew)#僅僅是y值 100*100的值

# 繪圖
# 為了更明顯地比較插值前后的區別，使用關鍵字參數interpolation='nearest'
# 關閉imshow()內置的插值運算。
pl.subplot(121)
im1=pl.imshow(fvals, extent=[-1,1,-1,1], cmap=mpl.cm.hot, interpolation='nearest', origin="lower")#pl.cm.jet
#extent=[-1,1,-1,1]為x,y范圍 favals為
pl.colorbar(im1)

pl.subplot(122)
im2=pl.imshow(fnew, extent=[-1,1,-1,1], cmap=mpl.cm.hot, interpolation='nearest', origin="lower")
pl.colorbar(im2)
pl.show()

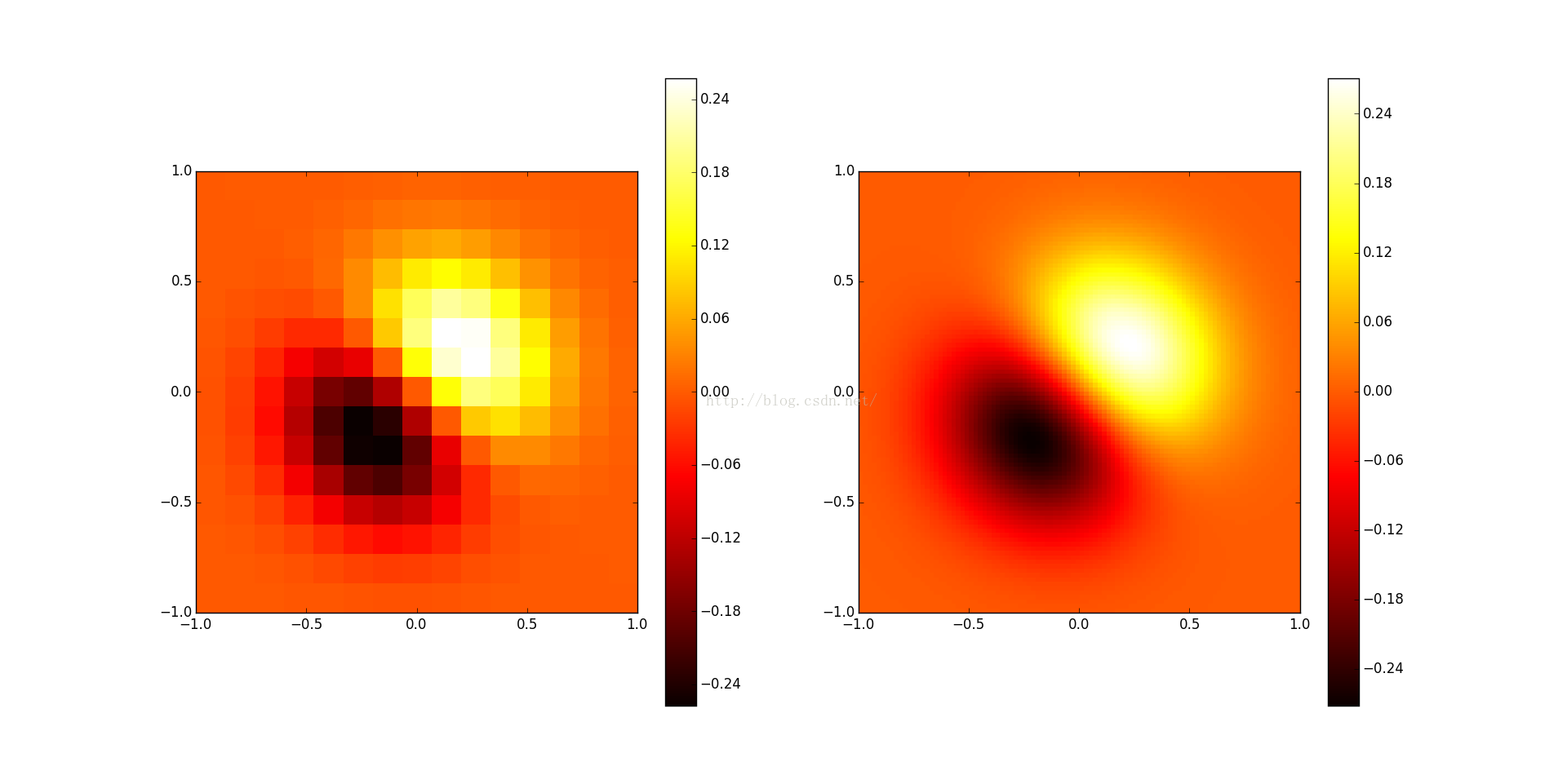
左圖為原始數據，右圖為二維插值結果圖。

二維插值的三維展示方法

# -*- coding: utf-8 -*-
"""
演示二維插值。
"""
# -*- coding: utf-8 -*-
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
from scipy import interpolate
import matplotlib.cm as cm
import matplotlib.pyplot as plt

def func(x, y):
 return (x+y)*np.exp(-5.0*(x**2 + y**2))

# X-Y軸分為20*20的網格
x = np.linspace(-1, 1, 20)
y = np.linspace(-1,1,20)
x, y = np.meshgrid(x, y)#20*20的網格數據

fvals = func(x,y) # 計算每個網格點上的函數值 15*15的值

fig = plt.figure(figsize=(9, 6))
#Draw sub-graph2
ax=plt.subplot(1, 2, 1,projection = '3d')
surf = ax.plot_surface(x, y, fvals, rstride=2, cstride=2, cmap=cm.coolwarm,linewidth=0.5, antialiased=True)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x, y)')
plt.colorbar(surf, shrink=0.5, aspect=5)#標注

#二維插值
newfunc = interpolate.interp2d(x, y, fvals, kind='cubic')#newfunc為一個函數

# 計算100*100的網格上的插值
xnew = np.linspace(-1,1,100)#x
ynew = np.linspace(-1,1,100)#y
fnew = newfunc(xnew, ynew)#僅僅是y值 100*100的值 np.shape(fnew) is 100*100
xnew, ynew = np.meshgrid(xnew, ynew)
ax2=plt.subplot(1, 2, 2,projection = '3d')
surf2 = ax2.plot_surface(xnew, ynew, fnew, rstride=2, cstride=2, cmap=cm.coolwarm,linewidth=0.5, antialiased=True)
ax2.set_xlabel('xnew')
ax2.set_ylabel('ynew')
ax2.set_zlabel('fnew(x, y)')
plt.colorbar(surf2, shrink=0.5, aspect=5)#標注

plt.show()

左圖的二維數據集的函數值由于樣本較少，會顯得粗糙。而右圖對二維樣本數據進行三次樣條插值，擬合得到更多數據點的樣本值，繪圖后圖像明顯光滑多了。

關于“使用python實現各種插值法的示例”這篇文章就分享到這里了，希望以上內容可以對大家有一定的幫助，使各位可以學到更多知識，如果覺得文章不錯，請把它分享出去讓更多的人看到。