您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章給大家分享的是有關C語言浮點函數中的modf和fmod怎么用的內容。小編覺得挺實用的,因此分享給大家做個參考,一起跟隨小編過來看看吧。
modf函數可以提取出浮點數的整數部分和小數部分。fmod函數可以返回兩個浮點數相除的余數。它們的函數原型如下:
double __cdecl modf(double _X,double *_Y); double __cdecl fmod(double _X,double _Y);
這兩個函數的功能看起來都挺簡單的,但是為什么在C語言庫中還要專門搞一個函數來計算呢?在使用這兩個函數之前,首先看一個簡單的浮點數相關的例子。
int main ()
{
int i;
float j=1.0;
for(i=0; i<100; i++)
{
j+=0.1;
printf("%f \n",j);
}
return(0);
}給一個浮點數1.0每次累加0.1,總共累加100,感覺就是一個簡單的加法運算,它的輸出結果肯定也知道是什么了,下面來運行一下這個代碼,輸出結果如下:
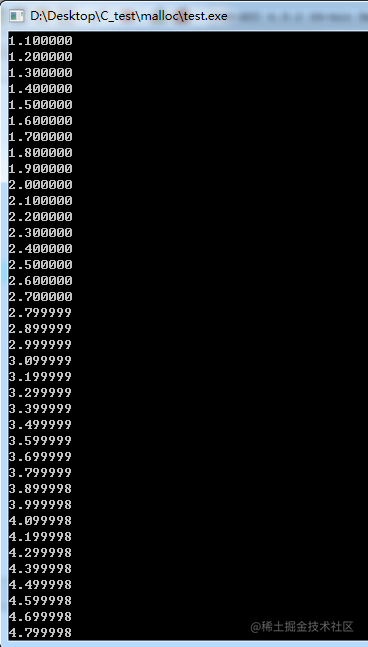
看到結果的第一眼,是不是感覺計算機算錯了?怎么算著算著結果還給跑偏了。其實計算機并沒有算錯,程序運行的結果也是正確的。這里使用一個在線浮點數轉換工具驗證一下。
首先看一下浮點數1.0在內存的存儲情況。
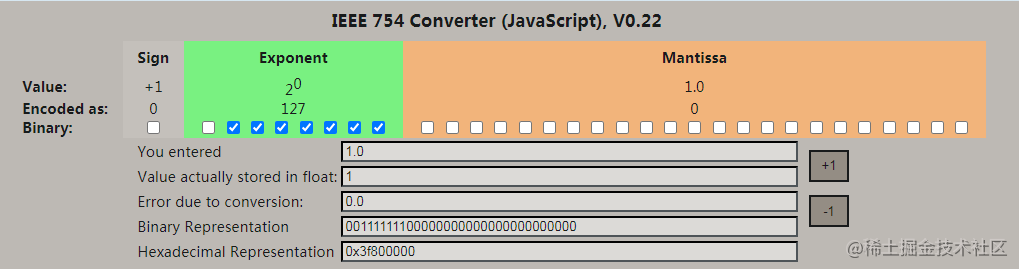
再看一下浮點數2.8在內存的存儲情況。
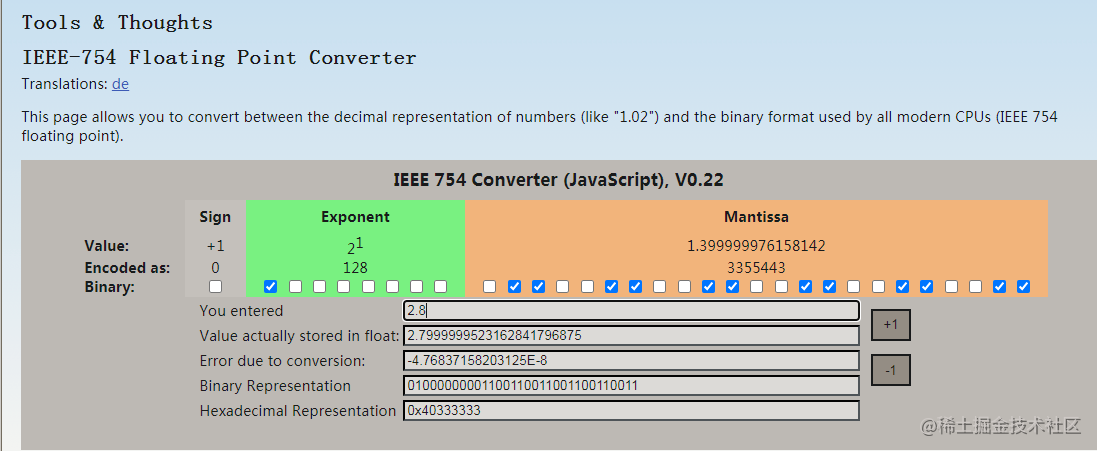
通過對比可以看出1.0的實際存儲值是1,和真實值是一樣的。2.8的實際存儲值是2.7999999523162841796875,和真實值已經產生了一點誤差。那么這個誤差是什么引起的呢?這里就要從浮點數的存儲原理說起了。
通在C語言中,一個浮點數占32位,其中第一位表示符號位,0表示正數,1表示負數。緊接著8位表示指數部分,也就是系統會將浮點數表示為指數計數法,這8位就是指數部分的值,但是這里的指數是以2為底的。剩下的23位表示的就是尾數,也就是有效數據。
由于小數部分都是通過 2^a+2^b+2^c.......2^n 這種指數的累加來實現的,而指數的累加不一定可以百分百的等于原值,它只可能無限的接近原值。所以對于浮點數的操作不是像整數那樣簡單,為了保證操作浮點數時的精度,所以C語言的庫函數才給我們提供了這兩種浮點數操作的函數,方便使用。
接下來看一下modf函數的用法。
#include <stdio.h>
#include <math.h>
int main ()
{
double x, fractpart, intpart;
x = 8.123456;
fractpart = modf(x, &intpart);
printf("整數部分= %lf\n", intpart);
printf("小數部分 = %lf \n", fractpart);
return(0);
}modf函數有兩個參數,第一個參數時待操作的浮點數,第二個參數用來存儲浮點數的整數部分,它的返回值是浮點數的小數部分。
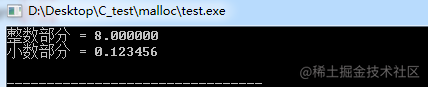
通過輸出結果可以看到,浮點數的整數部分和小數部分精度都沒有丟失。
再看一下fmod函數的用法。
#include <stdio.h>
#include <math.h>
int main ()
{
float a, b;
int c;
a = 9.0;
b = 3.7;
c = 2;
printf("%f / %f 的余數是 %lf\n", a, b, fmod(a,b));
printf("%f / %d 的余數是 %lf\n", a, c, fmod(a,c));
return(0);
}fmod函數有兩個參數,第一個參數是分子,第二個參數是分母,它返回第一個參數除以第二個參數的余數。

通過輸出的結果可以看到,浮點數的精度沒有丟失。
感謝各位的閱讀!關于“C語言浮點函數中的modf和fmod怎么用”這篇文章就分享到這里了,希望以上內容可以對大家有一定的幫助,讓大家可以學到更多知識,如果覺得文章不錯,可以把它分享出去讓更多的人看到吧!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。