C語言的dp算法LeetCode炒股習題案例分析

本文小編為大家詳細介紹“C語言的dp算法LeetCode炒股習題案例分析”，內容詳細，步驟清晰，細節處理妥當，希望這篇“C語言的dp算法LeetCode炒股習題案例分析”文章能幫助大家解決疑惑，下面跟著小編的思路慢慢深入，一起來學習新知識吧。

概念

說到動態規劃，什么是動態規劃？

動態規劃（英語：Dynamic programming，簡稱 dp）通過把原問題分解為相對簡單的子問題的方式求解復雜問題的方法。動態規劃常常適用于有重疊子問題和最優子結構性質的問題。

看著這么復雜哈，其實總結出來就是大事化小，拆分成小問題但是這些小問題和原問題是同質的，動規致力于解決每一個子問題，減少計算，其實和遞歸思想，分治法有些類似，斐波那契數列就可以看做入門級的經典動規問題

這里引用一個網上流行的例子來給大家體會一下：

A ：“1+1+1+1+1+1+1+1 =？”
A ：“上面等式的值是多少”
B ：計算 “8”
A : 在上面等式的左邊寫上 “1+” 呢？
A : “此時等式的值為多少”
B : 很快得出答案 “9”
A : “你怎么這么快就知道答案了”
A : “只要在8的基礎上加1就行了”
A : “所以你不用重新計算，因為你記住了第一個等式的值為8!動態規劃算法也可以說是 ‘記住求過的解來節省時間’”

性質

1.最優化原理：如果問題的最優解所包含的子問題的解也是最優的，就稱該問題具有最優子結構，即滿足最優化原理（說人話就是切大瓜，切到最小又不影響我體驗）

2.有重疊子問題：即子問題之間是不獨立的，一個子問題在下一階段決策中可能被多次使用到（說人話就是藕斷絲連，拿一個可能帶動其他）

3.無后效性：即某階段狀態一旦確定，就不受這個狀態以后決策的影響。也就是說，某狀態以后的過程不會影響以前的狀態，只與當前狀態有關（說人話就是把水化成冰，但本質上依然是水）

典型特征

動態規劃有4個典型特征：

1.最優子結構

2.狀態轉移方程

3.邊界

4.重疊子問題

以我們熟悉的斐波那契數列為例

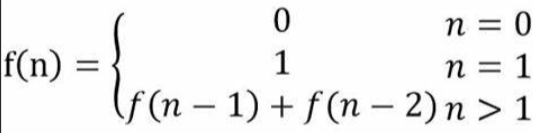
f(n-1)和f(n-2) 稱為 f(n) 的最優子結構，f(n)= f（n-1）+f（n-2）就稱為狀態轉移方程，f(1) = 1, f(2) = 2 稱為邊界，其中f(5)= f(4)+f(3),f(4) = f(3) + f(2) ,f(3)就是重疊子問題。

實戰論證

要學習dp算法就一定得談談 LeetCode 里面的鼻祖題——炒股系列問題，我們就拿例題來港港怎么理解他的典型特征

初始題比較簡單，我們以 II 為例：

示例：
輸入: prices = [7,1,5,3,6,4]
輸出: 7

小捷徑

看到這里其實最簡單的方法已經明了了，那就是貪心算法，只要能賺，只要不賠我就買買買！你說我貪不貪心？

int maxProfit(int* prices, int pricesSize) {
    int sum = 0;
    for (int i = 1; i < pricesSize; ++i) {
        sum += fmax(0, prices[i] - prices[i - 1]);
    }
    return sum;
}

這里用了一個庫函數 fmax ，需要引頭文件<math.h>，用于比較兩個參數的最大值，語法是：

type fmax  (參數1 , 參數2);

再介紹一種我自己用的方法，和貪心原理上差不多，只是用的普普通通的遍歷：

int maxProfit(int* prices, int pricesSize) {
	int n = 0;
	if (pricesSize == 0)
	{
		return 0;
	}
	int sum = 0;
	while (n < pricesSize - 1)
	{
		for (n = 0; n < pricesSize - 1; n++)
			if (prices[n + 1] - prices[n] > 0)//保證買賣能賺就入手
			{
				sum += prices[n+1]-prices[n];
			}
	}
	return sum;
}

我自己的方法還是比較優的

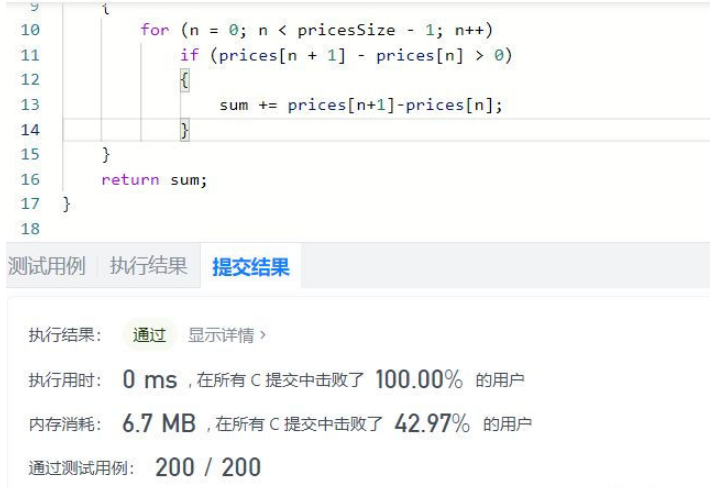
這樣就能一套帶走，但我們要用 dp 去搞定他，dp 其實也很簡單，只是看著有點復雜，咱不能望而卻步是吧。

分析條件，題目中說不能多次買賣，那我們有且只有兩種狀態就是沒有和有一支，沒有就是手里為0，又有兩種可能就是前一天就是 0 和這一天有一支但被賣出去了；同理，有一支的情況就是前一天就有一支和前一天兩手空空但我今天買進了一支。以此我們寫出求最大利潤的狀態轉移方程( i 從 0 開始)：

第i天有0支股票：dp[i][0] = dp[i-1][0] + dp[i][1]+prices[i];
第i天有1支股票：dp[i][1] = dp[i-1][1] + dp[i-1][0]-prices[i];

狀態轉移方程寫出來了，題目就迎刃而解了

算法實現

1、借助數組或者二維數組，保存每一個子問題的結果，具體創建數組還是二維數組看題目而定，比如找零錢問題中的不同面值零錢與總錢數，這樣就需要創建一個二維數組

2、對應題干條件，具體要求來設置數組邊界值,一維數組就是設置第一個數字，二維數組就是設置第一行跟第一列的值

3、找出狀態轉換方程，找到每個狀態跟他上一個狀態的關系，根據狀態轉化方程就可以寫出代碼

我們用剛剛推出來的狀態轉移方程就可以寫出整個代碼框架：

int maxProfit(int* prices, int pricesSize) {
    int sz = pricesSize;
    int i = 0;
    int dp[sz][2] = 0; //sz是最大買賣天數內的價格，2代表兩種狀態0和1
    dp[0][0] = 0,dp[0][1]=-prices[0];//設置邊界值
    for(i=0;i<sz;i++)
    {
    dp[i][0] = fmax(dp[i-1][0] + dp[i][1]+prices[i]);
    dp[i][1] = fmax(dp[i-1][1] + dp[i-1][0]-prices[i]);//兩種狀態分別求最大利潤
    }
    return [sz-1][0];
  }

優化

我們不難發現，我們的收益只和股票前一天的價格掛鉤，和更早的狀態沒有關系，那我們為了減小時間復雜度和空間復雜度，可以將二維數組轉化成一維滾動數組搞定

int maxProfit(int* prices, int pricesSize) {
    int dp[pricesSize][2];
    int dp0 = 0;dp1 = -prices[0];
    for (int i = 1; i < pricesSize; ++i)
     {
       int Dp0 = fmax(dp0, dp1+prices[i]);
        Dp1 = fmax(dp1, dp0-prices[i]); //同理轉換出狀態轉移方程
    }
    dp0 = Dp0;
    dp1 = Dp1;//滾動更新dp0和dp1
    return dp[pricesSize - 1][0];
}

讀到這里，這篇“C語言的dp算法LeetCode炒股習題案例分析”文章已經介紹完畢，想要掌握這篇文章的知識點還需要大家自己動手實踐使用過才能領會，如果想了解更多相關內容的文章，歡迎關注億速云行業資訊頻道。