JavaScript中棧和隊列算法的案例分析

這篇文章主要介紹JavaScript中棧和隊列算法的案例分析，文中介紹的非常詳細，具有一定的參考價值，感興趣的小伙伴們一定要看完！

一、認識數據結構

什么是數據結構？下面是維基百科的解釋

數據結構是計算機存儲、組織數據的方式

數據結構意味著接口或封裝：一個數據結構可被視為兩個函數之間的接口，或者是由數據類型聯合組成的存儲內容的訪問方法封裝

我們每天的編碼中都會用到數據結構，因為數組是最簡單的內存數據結構，下面是常見的數據結構

• 數組（Array）

• 棧（Stack）

• 隊列（Queue）

• 鏈表（Linked List）

• 樹（Tree）

• 圖（Graph）

• 堆（Heap）

• 散列表（Hash）

下面來學習學習棧和隊列..

二、棧

2.1 棧數據結構

棧是一種遵循后進先出（LIFO）原則的有序集合。新添加的或待刪除的元素都保存在棧的同一端，稱作棧頂，另一端就叫棧底。在棧里，新元素都接近棧頂，舊元素都接近棧底。

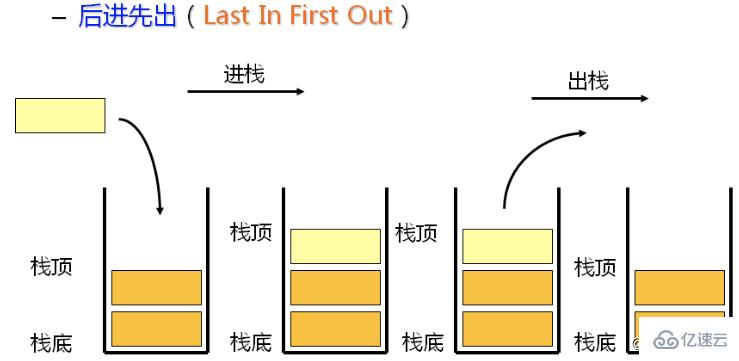
類比生活中的物件：一摞書或者推放在一起的盤子

2.2 棧的實現

普通的棧常用的有以下幾個方法：

push 添加一個（或幾個）新元素到棧頂

pop 溢出棧頂元素，同時返回被移除的元素

peek 返回棧頂元素，不對棧做修改

isEmpty 棧內無元素返回true，否則返回false

size 返回棧內元素個數

clear 清空棧

class Stack {
  constructor() {
    this._items = []; // 儲存數據
  }
  // 向棧內壓入一個元素
  push(item) {
    this._items.push(item);
  }
  // 把棧頂元素彈出
  pop() {
    return this._items.pop();
  }
  // 返回棧頂元素
  peek() {
    return this._items[this._items.length - 1];
  }
  // 判斷棧是否為空
  isEmpty() {
    return !this._items.length;
  }
  // 棧元素個數
  size() {
    return this._items.length;
  }
  // 清空棧
  clear() {
    this._items = [];
  }
}

現在再回頭想想數據結構里面的棧是什么。

突然發現并沒有那么神奇，僅僅只是對原有數據進行了一次封裝而已。而封裝的結果是：并不去關心其內部的元素是什么，只是去操作棧頂元素，這樣的話，在編碼中會更可控一些。

2.3 棧的應用

（1）十進制轉任意進制

要求: 給定一個函數，輸入目標數值和進制基數，輸出對應的進制數（最大為16進制）

baseConverter(10, 2) ==> 1010
baseConverter(30, 16) ==> 1E

分析: 進制轉換的本質：將目標值一次一次除以進制基數，得到的取整值為新目標值，記錄下余數，直到目標值小于0，最后將余數逆序組合即可。利用棧，記錄余數入棧，組合時出棧

// 進制轉換
function baseConverter(delNumber, base) {
  const stack = new Stack();
  let rem = null;
  let ret = [];
  // 十六進制中需要依次對應A~F
  const digits = '0123456789ABCDEF';

  while (delNumber > 0) {
    rem = Math.floor(delNumber % base);
    stack.push(rem);
    delNumber = Math.floor(delNumber / base);
  }

  while (!stack.isEmpty()) {
    ret.push(digits[stack.pop()]);
  }

  return ret.join('');
}

console.log(baseConverter(100345, 2)); //輸出11000011111111001
console.log(baseConverter(100345, 8)); //輸出303771
console.log(baseConverter(100345, 16)); //輸出187F9

（2）逆波蘭表達式計算

要求: 逆波蘭表達式，也叫后綴表達式，它將復雜表達式轉換為可以依靠簡單的操作得到計算結果的表達式，例如(a+b)*(c+d)轉換為a b + c d + *

["4", "13", "5", "/", "+"] ==> (4 + (13 / 5)) = 6
["10", "6", "9", "3", "+", "-11", "*", "/", "*", "17", "+", "5", "+"]
==> ((10 * (6 / ((9 + 3) * -11))) + 17) + 5

分析: 以符號為觸發節點，一旦遇到符號，就將符號前兩個元素按照該符號運算，并將新的結果入棧，直到棧內僅一個元素

function isOperator(str) {
  return ['+', '-', '*', '/'].includes(str);
}
// 逆波蘭表達式計算
function clacExp(exp) {
  const stack = new Stack();
  for (let i = 0; i < exp.length; i++) {
    const one = exp[i];
    if (isOperator(one)) {
      const operatNum1 = stack.pop();
      const operatNum2 = stack.pop();
      const expStr = `${operatNum2}${one}${operatNum1}`;
      const res = eval(expStr);
      stack.push(res);
    } else {
      stack.push(one);
    }
  }
  return stack.peek();
}
console.log(clacExp(["4", "13", "5", "/", "+"])); // 6.6

（3）利用普通棧實現一個有min方法的棧

思路: 使用兩個棧來存儲數據，其中一個命名為dataStack，專門用來存儲數據，另一個命名為minStack，專門用來存儲棧里最小的數據。始終保持兩個棧中的元素個數相同，壓棧時判別壓入的元素與minStack棧頂元素比較大小，如果比棧頂元素小，則直接入棧，否則復制棧頂元素入棧；彈出棧頂時，兩者均彈出即可。這樣minStack的棧頂元素始終為最小值。

class MinStack {
  constructor() {
    this._dataStack = new Stack();
    this._minStack = new Stack();
  }

  push(item) {
    this._dataStack.push(item);
    // 為空或入棧元素小于棧頂元素，直接壓入該元素
    if (this._minStack.isEmpty() || this._minStack.peek() > item) {
      this._minStack.push(item);
    } else {
      this._minStack.push(this._minStack.peek());
    }
  }

  pop() {
    this._dataStack.pop();
    return this._minStack.pop();
  }

  min() {
    return this._minStack.peek();
  }
}

const minstack = new MinStack();

minstack.push(3);
minstack.push(4);
minstack.push(8);
console.log(minstack.min()); // 3
minstack.push(2);
console.log(minstack.min()); // 2

三、隊列

3.1 隊列數據結構

隊列是遵循先進先出（FIFO，也稱為先來先服務）原則的一組有序的項。隊列在尾部添加新元素，并從頂部移除元素。最新添加的元素必須排在隊列的末尾

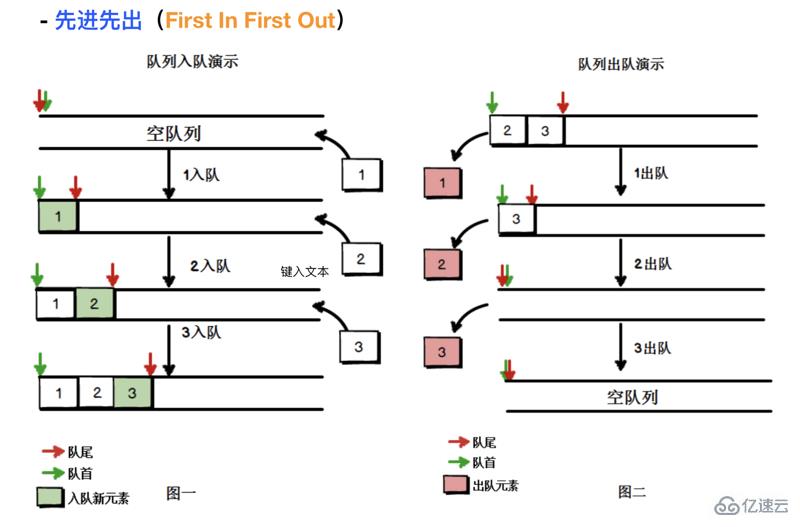
類比：日常生活中的購物排隊

3.2 隊列的實現

普通的隊列常用的有以下幾個方法：

• enqueue 向隊列尾部添加一個(或多個)新的項

• dequeue 移除隊列的第一(即排在隊列最前面的)項，并返回被移除的元素

• head 返回隊列第一個元素，隊列不做任何變動

• tail 返回隊列最后一個元素，隊列不做任何變動

• isEmpty 隊列內無元素返回true，否則返回false

• size 返回隊列內元素個數

• clear 清空隊列

class Queue {
  constructor() {
    this._items = [];
  }

  enqueue(item) {
    this._items.push(item);
  }

  dequeue() {
    return this._items.shift();
  }

  head() {
    return this._items[0];
  }

  tail() {
    return this._items[this._items.length - 1];
  }

  isEmpty() {
    return !this._items.length;
  }

  size() {
    return this._items.length;
  }

  clear() {
    this._items = [];
  }
}

與棧類比，棧僅能操作其頭部，隊列則首尾均能操作，但僅能在頭部出尾部進。當然，也印證了上面的話：棧和隊列并不關心其內部元素細節，也無法直接操作非首尾元素。

3.3 隊列的應用

（1）約瑟夫環（普通模式）

要求: 有一個數組a[100]存放0~99；要求每隔兩個數刪掉一個數，到末尾時循環至開頭繼續進行，求最后一個被刪掉的數。

分析: 按數組創建隊列，依次判斷元素是否滿足為指定位置的數，如果不是則enqueue到尾部，否則忽略，當僅有一個元素時便輸出

// 創建一個長度為100的數組
const arr_100 = Array.from({ length: 100 }, (_, i) => i*i);

function delRing(list) {
  const queue = new Queue();
  list.forEach(e => { queue.enqueue(e); });
  
  let index = 0;
  while (queue.size() !== 1) {
    const item = queue.dequeue();
    index += 1;
    if (index % 3 !== 0) {
      queue.enqueue(item);
    }
  }

  return queue.tail();
}

console.log(delRing(arr_100)); // 8100 此時index=297

（2）菲波那切數列（普通模式）

要求: 使用隊列計算斐波那契數列的第n項
分析: 斐波那契數列的前兩項固定為1，后面的項為前兩項之和，依次向后，這便是斐波那契數列。

function fibonacci(n) {
    const queue = new Queue();
    queue.enqueue(1);
    queue.enqueue(1);
    
    let index = 0;
    while(index < n - 2) {
        index += 1;
        // 出隊列一個元素
        const delItem = queue.dequeue();
        // 獲取頭部值
        const headItem = queue.head();
        const nextItem = delItem + headItem;
        queue.enqueue(nextItem);
    }
    
    return queue.tail();
}

console.log(fibonacci(9)); // 34

（3）用隊列實現一個棧

要求: 用兩個隊列實現一個棧
分析: 使用隊列實現棧最主要的是在隊列中找到棧頂元素并對其操作。具體的思路如下：

1. 兩個隊列，一個備份隊列emptyQueue，一個是數據隊列dataQueue；

2. 在確認棧頂時，依次dequeue至備份隊列，置換備份隊列和數據隊列的引用即可

class QueueStack {
  constructor() {
    this.queue_1 = new Queue();
    this.queue_2 = new Queue();
    this._dataQueue = null; // 放數據的隊列
    this._emptyQueue = null; // 空隊列,備份使用
  }

  // 確認哪個隊列放數據,哪個隊列做備份空隊列
  _initQueue() {
    if (this.queue_1.isEmpty() && this.queue_2.isEmpty()) {
      this._dataQueue = this.queue_1;
      this._emptyQueue = this.queue_2;
    } else if (this.queue_1.isEmpty()) {
      this._dataQueue = this.queue_2;
      this._emptyQueue = this.queue_1;
    } else {
      this._dataQueue = this.queue_1;
      this._emptyQueue = this.queue_2;
    }
  };

  push(item) {
    this.init_queue();
    this._dataQueue.enqueue(item);
  };

  peek() {
    this.init_queue();
    return this._dataQueue.tail();
  }

  pop() {
    this.init_queue();
    while (this._dataQueue.size() > 1) {
      this._emptyQueue.enqueue(this._dataQueue.dequeue());
    }
    return this._dataQueue.dequeue();
  };
};

學習了棧和隊列這類簡單的數據結構，我們會發現。數據結構并沒有之前想象中那么神秘，它們只是規定了這類數據結構的操作方式：棧只能對棧頂進行操作，隊列只能在尾部添加在頭部彈出；且它們不關心內部的元素狀態。

以上是“JavaScript中棧和隊列算法的案例分析”這篇文章的所有內容，感謝各位的閱讀！希望分享的內容對大家有幫助，更多相關知識，歡迎關注億速云行業資訊頻道！