您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
小編給大家分享一下Linux中RAID 6如何實現Q校驗算法,相信大部分人都還不怎么了解,因此分享這篇文章給大家參考一下,希望大家閱讀完這篇文章后大有收獲,下面讓我們一起去了解一下吧!
RAID即獨立磁盤冗余陣列,簡稱為「磁盤陣列」,其實就是用多個獨立的磁盤組成在一起形成一個大的磁盤系統,從而實現比單塊磁盤更好的存儲性能和更高的可靠性。

RAID 6是指帶有兩種分布存儲的奇偶校驗碼(既P和Q)的獨立硬盤結構。與RAID 5相比,RAID 6增加了第二個獨立校驗碼(Q)信息塊,兩個獨立的奇偶校驗系統使用不同的算法,數據的可靠性非常高,即使兩塊硬盤同時失效也不會影響數據的使用,主要是用于要求數據絕對安全的場合。如下圖: 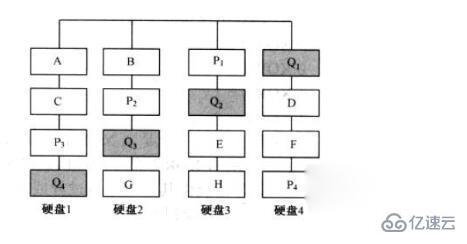 上圖中Q為RAID 6的第二個校驗信息塊,采用的是非常復雜的“伽羅華域”算法,稍后會講到。
上圖中Q為RAID 6的第二個校驗信息塊,采用的是非常復雜的“伽羅華域”算法,稍后會講到。
其實RAID 6的P校驗和RAID 5的校驗是一樣的,都是采用的“異或”運算。異或運算符的原則就是相同為0,不同為1的。在RAID 5的環境中只能掉一塊硬盤,但是RAID 6在RAID 5的基礎上添加了Q校驗,因此RAID 6支持同時掉兩塊盤。異或運算如下:
P = A + B + C = A xor B xor C A = P - B - C = P xor B xor C
注意:上述的加減法都是異或運算。
說到Q校驗就有點復雜了,它采用上面所提到的“伽羅華域”算法。“伽羅華域”實際上就是“0-255”的一個有限域GF(2^8),在GF(2^8)內不管是是加、減、乘、除都不會超過這個范圍。并且,加減法可逆,乘除法可逆,而且計算的值在GF(2^8)內是唯一的。注意:此處提到的加、減、乘、除法不是日常使用的加減乘除,而是“伽羅華域”內的運算。在GF(2^8)中,如果2的n次方大于某個值(本原多項式)就會對該值(本原多項式)取余,結果又會返回到GF(2^8)中。因此,保證了2^0到2^255的結果值在GF(2^8)內是唯一的。 在GF(2^8)中一共有16個本原多項式,分別如下:
1 x8+x7+x6+x5+x4+x2+1 1 1111 0101 = 0x1F5 2 x8+x7+x6+x5+x2+x+1 1 1110 0111 = 0x1E7 3 x8+x7+x6+x3+x2+x+1 1 1100 1111 = 0x1CF 4 x8+x7+x6+x+1 1 1100 0011 = 0x1C3 5 x8+x7+x5+x3+1 1 1010 1001 = 0x1A9 6 x8+x7+x3+x2+1 1 1000 1101 = 0x18D 7 x8+x7+x2+x+1 1 1000 0111 = 0x187 8 x8+x6+x5+x4+1 1 0111 0001 = 0x171 9 x8+x6+x5+x3+1 1 0110 1001 = 0x169 10 x8+x6+x5+x2+1 1 0110 0101 = 0x165 11 x8+x6+x5+x+1 1 0110 0011 = 0x163 12 x8+x6+x4+x3+x2+x+1 1 0101 1111 = 0x15F 13 x8+x6+x3+x2+1 1 0100 1101 = 0x14D 14 x8+x5+x3+x2+1 1 0010 1101 = 0x12D 15 x8+x5+x3+x+1 1 0010 1011 = 0x12B 16 x8+x4+x3+x2+1 1 0001 1101 = 0x11D
RAID 6常用的本原多項式為0X11D,既上列中最后一個。Linux 環境中的RAID 6也是如此。 好了回到Q校驗上,Q校驗和P校驗結合正好組成了一個二元一次方程,K1、K2、K3為GF(2^8)中多項式的數值。
P = A + B + C Q = A*K1 + B*K2 + C*K3
伽羅華域中的加減法也是異或運算,所以就不做詳細解釋了,重點解釋一下乘除法。通過上面的Q校驗知道Q校驗的生成需要伽羅華域中的乘法運算,計算乘法運算是一件非常復雜的事情,最好的解決辦法就是將GF(2^8)中所有多項式的值生成表格,通過查表得知乘法運算的值。
1、生成正表GFILOG
通過下表的方法生成正表GFILOG,注意:此表的本原多項式為0X11D。  如下:是正表GFILOG
如下:是正表GFILOG 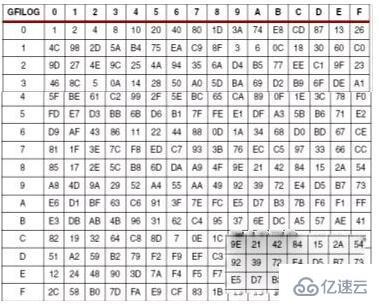
2、生成反表GFLOG
有了正向變換表,要得到逆向表就很簡單了,把正向中的表變換值做為索引,在把正向表中的索引作為值就OK了。如下表: 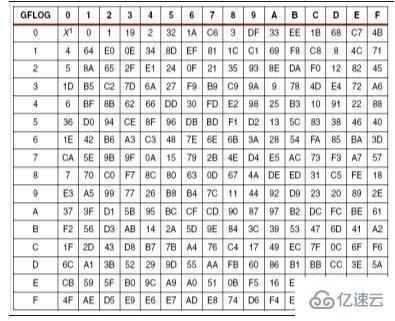
3、計算乘除法運算(查表法)
乘法:A * K1 = GFILOG[(GFLOG[A]+GFLOG[K1]) mod 255]; 除法:A / K1 = GFILOG[(GFLOG[A]-GFLOG[K1]+255) mod 255];
現在知道了伽羅華域的乘除法,那么我們計算Q校驗就方便了許多。
當RAID 6中壞掉兩塊磁盤,那該如何生成丟失的數據呢?用RAID 6的一個條帶舉例說明。 1、如果某個條帶中丟失的兩塊數據是P和Q,那么正好,數據沒有丟失,正常提取即可。 2、如果某個條帶中丟失的兩塊數據是P和A,那么可以根據Q校驗計算出A的數據。
P = A*K1 + B*K2 + C*K3 A*K1 = P + B*K2 + C*K3 A = (P + B*K2 + C*K3)/ K1 //注:K1可以同過查表獲取
3、如果某個條帶中丟失的兩塊數據是Q和A,那么可以根據校驗P計算出A的數據。
P = A + B + C A = P + B + C
4、如果某個條帶中丟失的兩塊數據是A和B,那么可以根據校驗P和Q計算出A和B的數據。
P = A + B + C Q = A*K1 + B*K2 + C*K3 A = P + B + C Q = (P + B + C)*K1 + B*K2 +C*K3 Q = P*K1 + B*K1 + C*K1 + B*K2 + C*K3 Q = P*K1 + C*K1 + C*K3 + B*K1 + B*K2 Q + P*K1 + C*K1 + C*K3 = (K1+K2) * B B = ( Q + P*K1 + C*K1 + C*K3) / (K1+K2)
計算出B的值以后,再根據P校驗和計算出A的值就容易很多了。
A = P + B + C
根據前的內容已經知道RAID 6的大致原理了。因為伽羅華域的本原多項式有16種,因此RAID 6的種類有很多,再加上K值的不固定。因此計算某個RAID 6的Q校驗值會變的很復雜。不過Linux環境下的RAID 6的K值經過測試,其值根據夠成RAID 6陣列的磁盤數,從本原多項式0X11D的開始取(RAID 6總磁盤數 -2)個多項式的值作為K的值。
以上是“Linux中RAID 6如何實現Q校驗算法”這篇文章的所有內容,感謝各位的閱讀!相信大家都有了一定的了解,希望分享的內容對大家有所幫助,如果還想學習更多知識,歡迎關注億速云行業資訊頻道!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。