Java怎么實現二叉搜索樹的插入、刪除功能

這篇文章給大家介紹Java怎么實現二叉搜索樹的插入、刪除功能，內容非常詳細，感興趣的小伙伴們可以參考借鑒，希望對大家能有所幫助。

Java的特點有哪些

Java的特點有哪些 1.Java語言作為靜態面向對象編程語言的代表，實現了面向對象理論，允許程序員以優雅的思維方式進行復雜的編程。 2.Java具有簡單性、面向對象、分布式、安全性、平臺獨立與可移植性、動態性等特點。 3.使用Java可以編寫桌面應用程序、Web應用程序、分布式系統和嵌入式系統應用程序等。

二叉樹的結構

public class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode() {
        }
        TreeNode(int val) {
            this.val = val;
        }
    }

中序遍歷

• 中序遍歷：從根節點開始遍歷，遍歷順序是：左子樹->當前節點->右子樹，在中序遍歷中，對每個節點來說：

只有當它的左子樹都被遍歷過了（或者沒有左子樹），它才會被遍歷到。
在遍歷右子樹之前，一定會先遍歷當前節點。

• 中序遍歷得到的第一個節點是沒有左子樹的（也許是葉子節點，也許有右子樹）

• 同理，中序遍歷的最后一個節點沒有右子樹

代碼遞歸實現

List<TreeNode> list = new ArrayList<>();
    public void inorder_traversal(TreeNode root) {
        if (root == null) {
            return;
        }
        if (root.left != null) {
            inorder_traversal(root.left);
        }
        list.add(root);
        if (root.right != null) {
            inorder_traversal(root.right);
        }
    }

二叉搜索樹的定義

• 對每一個節點而言，左子樹的所有節點小于它，右子樹的所有節點大于它

• 二叉樹中每一個節點的值都不相同

• 中序遍歷的結果是升序的

這些定義決定了它的優點：查找效率快，因為二叉搜索樹查找一個值時，可以通過二分查找的方式，平均時間復雜度為log2(n),n是二叉樹的層樹

下圖就是一個標準的二叉搜索樹，右子樹比根節點大，左子樹比根節點小

查找節點

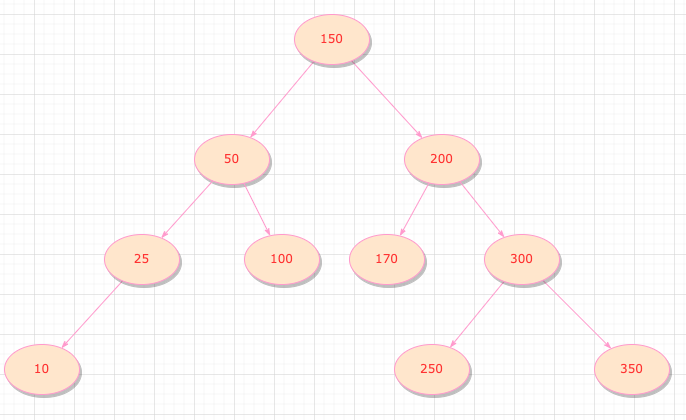
給定一個值，使用循環在二叉搜索樹中查找，找到該節點為止

• 從根節點開始，不斷循環進行比較

• 給定值大于當前節點，就找右子樹，小于就找左子樹，值相等就是找到了節點

代碼實現如下

public TreeNode search(TreeNode root, int val) {
        // 節點不為空，且不等于特定值
        while(root != null && root.val != val){
            if(root.val > val){
                root = root.left;
            }else{
                root = root.right;
            }
        }
        return root;
    }

添加節點

設要添加的節點為b， 二叉搜索樹的添加是將b作為葉子節點加入到其中，因為葉子節點的增加比較簡單。

• 跟搜索過程類似，從根節點開始，不斷循環找，找到一個適合新節點的位置

b值比當前節點大（小），并且當前節點的右（左）子樹為空，將b插入到當前節點的右（左）子樹中
如果當前節點的子樹不為空，繼續往下尋找

• 使用一個隨著搜索過程，不斷更新的pre節點作為b的父節點，由pre節點添加b

• 有可能要插入節點的二叉樹是一顆空樹，創建一個新的二叉樹

• 如果二叉搜索樹中已經有跟b相等的值，不需要進行添加

 public TreeNode insertInto(TreeNode root, int val) {
        
        if (root == null) {
            // 樹為空樹的情況
            return new TreeNode(val);
        }
        // 一個臨時節點指向根節點，用于返回值
        TreeNode tmp = root;
        TreeNode pre = root;
        
        while (root != null && root.val != val) {
            // 保存父節點
            pre = root;
            if (val > root.val) {
                root = root.right;
            } else {
                root = root.left;
            }
        }
        // 通過父節點添加
        if (val > pre.val) {
            pre.right = new TreeNode(val);
        } else {
            pre.left = new TreeNode(val);
        }
        return tmp;
    }

刪除節點

刪除過程比較復雜，先設二叉搜索樹要刪除的節點為a，a有以下三種情況

• a為葉子節點

• a有一個子節點

• a有兩個子節點刪除葉子節點

過程類似搜索節點，找到到a后，通過它的父節點刪除，并且葉子節點的刪除不影響樹的性質

有一個子節點的節點

要將a刪除，并且保留a的子節點，讓它的父節點連接它的子節點即可，因為a的子節點 與 a的父節點 關系 == a與 a的父節點 關系，所以不改變樹的性質

• 二叉搜索樹的定義決定了：對于每一個節點而言，它 大于（小于） 它的父節點，那么它的子節點 大于（小于） 它的父節點

過程像這張圖一樣

刪除有兩個子節點的節點

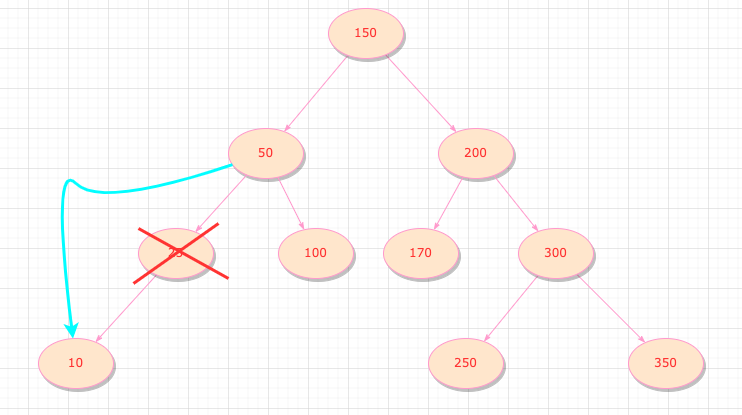
我們可以通過交換節點的方式，讓a 和 只有一個子節點的節點 交換，刪除a的操作就變成了上面第二種情況。

我們知道中序遍歷二叉搜索樹的結果是升序的，如果要交換，肯定要找中序遍歷在a左右兩邊的節點（因為值交換之后也滿足二叉搜索樹的定義）

• 中序遍歷的后（前）一個節點是右（左）子樹中序遍歷的第一個（最后一個）節點，而且它們都只有一個子節點

過程跟下面這張圖類似（a的值與中序遍歷的后一個節點交換，并刪除這個節點）

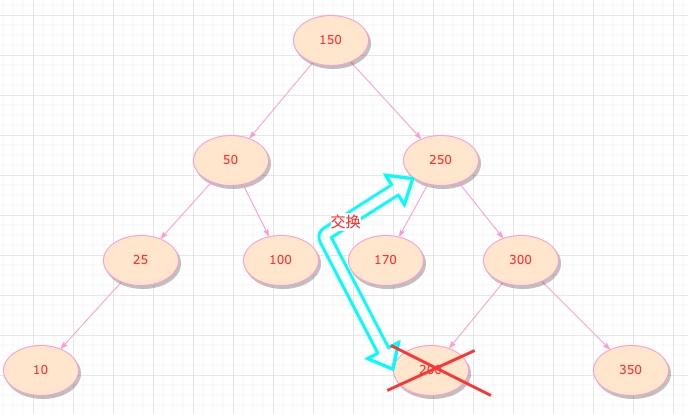
代碼實現

public TreeNode deleteNode(TreeNode root, int key) {
        TreeNode tmp = root;
        TreeNode pre = root;
        // 尋找要刪除的節點
        while (root != null && root.val != key) {
            pre = root;
            if (key > root.val) {
                root = root.right;
            } else {
                root = root.left;
            }
        }
        // 找不到符合的節點值
        if (root == null) {
            return tmp;
        }
        // 只有一個子節點或者沒有子節點的情況
        if (root.left == null || root.right == null) {
            if (root.left == null) {
                // 要刪除的是根節點，返回它的子節點
                if (root == tmp) {
                    return root.right;
                }
                // 使用父節點連接子節點，實現刪除當前節點
                if (pre.left == root) {
                    pre.left = root.right;
                } else {
                    pre.right = root.right;
                }
            } else {
                if (root == tmp) {
                    return root.left;
                }
                if (pre.left == root) {
                    pre.left = root.left;
                } else {
                    pre.right = root.left;
                }
            }
            return tmp;
        }
        // 第一種方式
        // 尋找中序遍歷的后一個節點，也就是右子樹進行中序遍歷的第一個節點，右子樹的最左節點
        pre = root;
        TreeNode rootRight = root.right;
        while (rootRight.left != null) {
            pre = rootRight;
            rootRight = rootRight.left;
        }
        // 節點的值進行交換
        int tmpVal = rootRight.val;
        rootRight.val = root.val;
        root.val = tmpVal;
        // 中序遍歷的第一個節點肯定是沒有左子樹的，但是可能有右子樹，將右子樹連接到父節點上（相當于刪除有一個子節點的節點）
        if (pre.left == rootRight) {
            pre.left = rootRight.right;
        }else {
            pre.right = rootRight.right;
        }
        // 第二種方式
        // 尋找中序遍歷的前一個節點，也就是左子樹進行中序遍歷的最后一個節點，左子樹的最右節點
//        pre = root;
//        TreeNode rootLeft = root.left;
//        while (rootLeft.right != null){
//            pre = rootLeft;
//            rootLeft = rootLeft.right;
//        }
//
//        int tmpVal = rootLeft.val;
//        rootLeft.val = root.val;
//        root.val = tmpVal;
//
//        // 中序遍歷的最后一個節點肯定是沒有右子樹的，但是可能有左子樹，將左子樹連接到父節點上（相當于刪除有一個子節點的節點）
//        if (pre.left == rootLeft) {
//            pre.left = rootLeft.left;
//        }else {
//            pre.right = rootLeft.left;
//        }
        return tmp;
    }

關于Java怎么實現二叉搜索樹的插入、刪除功能就分享到這里了，希望以上內容可以對大家有一定的幫助，可以學到更多知識。如果覺得文章不錯，可以把它分享出去讓更多的人看到。