您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容主要講解“怎么用Python爬蟲預測今年雙十一銷售額”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“怎么用Python爬蟲預測今年雙十一銷售額”吧!
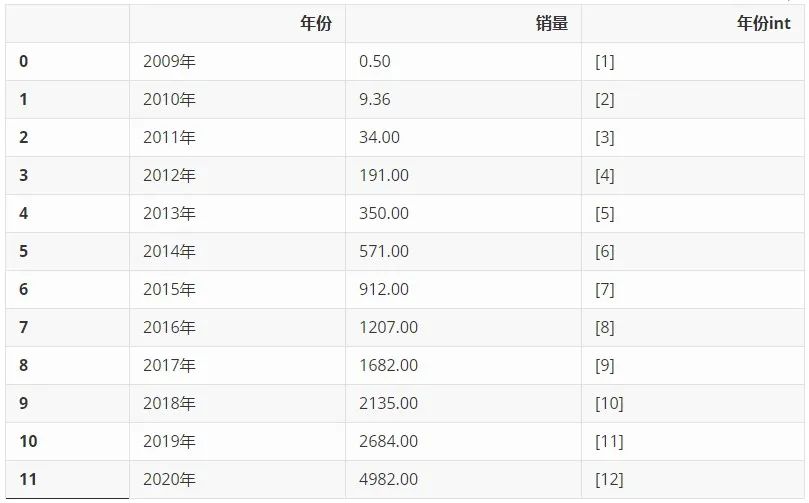
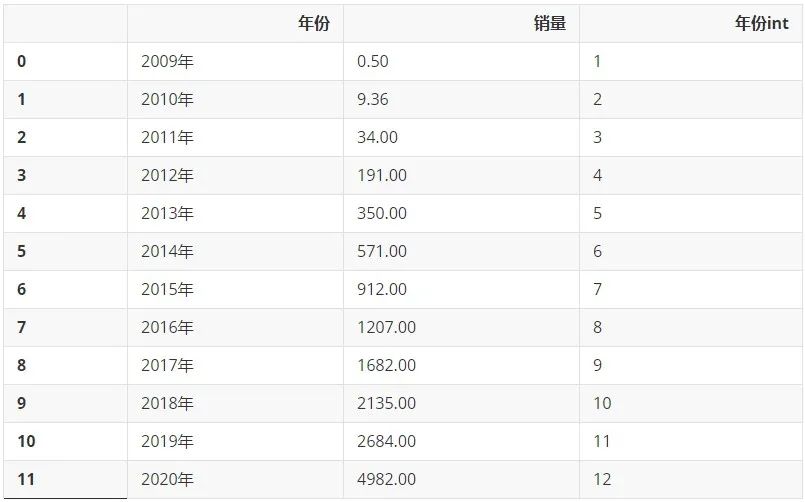
從網上搜集來歷年淘寶天貓雙十一銷售額數據,單位為億元,利用 Pandas 整理成 Dataframe,又添加了一列'年份int',留作后續的計算使用。
import pandas as pd
# 數據為網絡收集,歷年淘寶天貓雙十一銷售額數據,單位為億元,僅做示范
double11_sales = {'2009年': [0.50],
'2010年':[9.36],
'2011年':[34],
'2012年':[191],
'2013年':[350],
'2014年':[571],
'2015年':[912],
'2016年':[1207],
'2017年':[1682],
'2018年':[2135],
'2019年':[2684],
'2020年':[4982],
}
df = pd.DataFrame(double11_sales).T.reset_index()
df.rename(columns={'index':'年份',0:'銷量'},inplace=True)
df['年份int'] = [[i] for i in list(range(1,len(df['年份'])+1))]
df.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
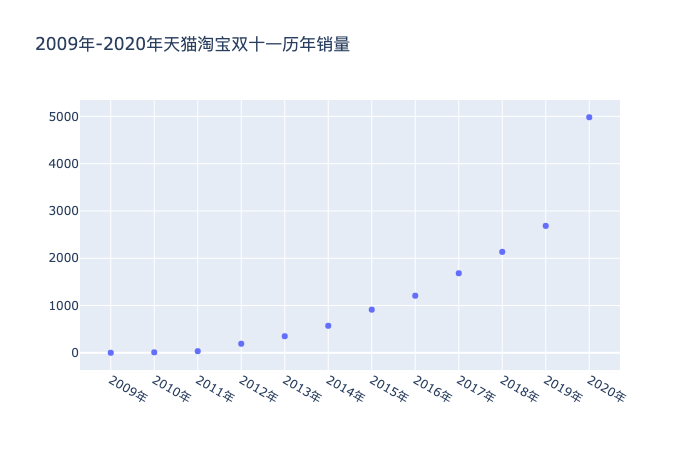
利用 plotly 工具包,將年份對應銷售量的散點圖繪制出來,可以明顯看到2020年的數據立馬飆升。
# 散點圖 import plotly as py import plotly.graph_objs as go import numpy as np year = df[:]['年份'] sales = df['銷量'] trace = go.Scatter( x=year, y=sales, mode='markers' ) data = [trace] layout = go.Layout(title='2009年-2020年天貓淘寶雙十一歷年銷量') fig = go.Figure(data=data, layout=layout) fig.show()
一元多次線性回歸
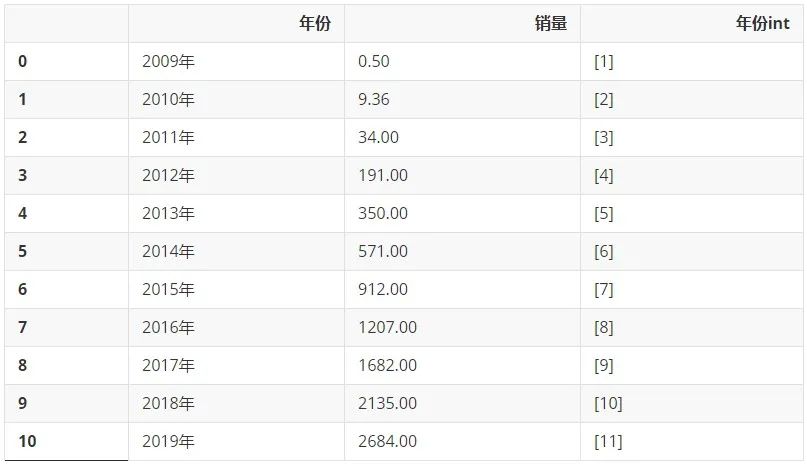
我們先來回顧一下2009-2019年的數據多么美妙。先只選取2009-2019年的數據:
df_2009_2019 = df[:-1] df_2009_2019
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
通過以下代碼生成二次項數據:
from sklearn.preprocessing import PolynomialFeatures poly_reg = PolynomialFeatures(degree=2) X_ = poly_reg.fit_transform(list(df_2009_2019['年份int']))
1.第一行代碼引入用于增加一個多次項內容的模塊 PolynomialFeatures
2.第二行代碼設置最高次項為二次項,為生成二次項數據(x平方)做準備
3.第三行代碼將原有的X轉換為一個新的二維數組X_,該二維數據包含新生成的二次項數據(x平方)和原有的一次項數據(x)
X_ 的內容為下方代碼所示的一個二維數組,其中第一列數據為常數項(其實就是X的0次方),沒有特殊含義,對分析結果不會產生影響;第二列數據為原有的一次項數據(x);第三列數據為新生成的二次項數據(x的平方)。
X_
array([[ 1., 1., 1.], [ 1., 2., 4.], [ 1., 3., 9.], [ 1., 4., 16.], [ 1., 5., 25.], [ 1., 6., 36.], [ 1., 7., 49.], [ 1., 8., 64.], [ 1., 9., 81.], [ 1., 10., 100.], [ 1., 11., 121.]])
from sklearn.linear_model import LinearRegression regr = LinearRegression() regr.fit(X_,list(df_2009_2019['銷量']))
LinearRegression()
1.第一行代碼從 Scikit-Learn 庫引入線性回歸的相關模塊 LinearRegression;
2.第二行代碼構造一個初始的線性回歸模型并命名為 regr;
3.第三行代碼用fit() 函數完成模型搭建,此時的regr就是一個搭建好的線性回歸模型。
接下來就可以利用搭建好的模型 regr 來預測數據。加上自變量是12,那么使用 predict() 函數就能預測對應的因變量有,代碼如下:
XX_ = poly_reg.fit_transform([[12]])
XX_
array([[ 1., 12., 144.]])
y = regr.predict(XX_) y
array([3282.23478788])
這里我們就得到了如果按照這個趨勢2009-2019的趨勢預測2020的結果,就是3282,但實際卻是4982億,原因就是上文提到的合并計算了,金額一下子變大了,繪制成圖,就是下面這樣:
# 散點圖 import plotly as py import plotly.graph_objs as go import numpy as np year = list(df['年份']) sales = df['銷量'] trace1 = go.Scatter( x=year, y=sales, mode='markers', name="實際銷量" # 第一個圖例名稱 ) XX_ = poly_reg.fit_transform(list(df['年份int'])+[[13]]) regr = LinearRegression() regr.fit(X_,list(df_2009_2019['銷量'])) trace2 = go.Scatter( x=list(df['年份']), y=regr.predict(XX_), mode='lines', name="擬合數據", # 第2個圖例名稱 ) data = [trace1,trace2] layout = go.Layout(title='天貓淘寶雙十一歷年銷量', xaxis_title='年份', yaxis_title='銷量') fig = go.Figure(data=data, layout=layout) fig.show()
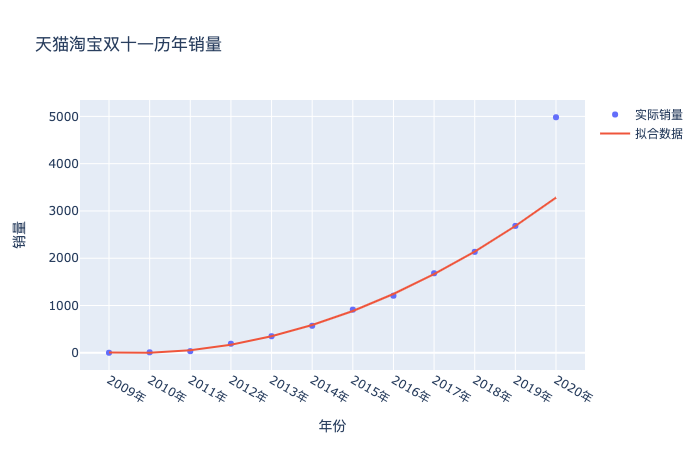
既然數據發生了巨大的偏離,咱們也別深究了,就大力出奇跡。同樣的方法,把2020年的真實數據納入進來,二話不說擬合一樣,看看會得到什么結果:
from sklearn.preprocessing import PolynomialFeatures poly_reg = PolynomialFeatures(degree=5) X_ = poly_reg.fit_transform(list(df['年份int']))
## 預測2020年 regr = LinearRegression() regr.fit(X_,list(df['銷量']))
LinearRegression()
XXX_ = poly_reg.fit_transform(list(df['年份int'])+[[13]])
# 散點圖 import plotly as py import plotly.graph_objs as go import numpy as np year = list(df['年份']) sales = df['銷量'] trace1 = go.Scatter( x=year+['2021年','2022年','2023年'], y=sales, mode='markers', name="實際銷量" # 第一個圖例名稱 ) trace2 = go.Scatter( x=year+['2021年','2022年','2023年'], y=regr.predict(XXX_), mode='lines', name="預測銷量" # 第一個圖例名稱 ) trace3 = go.Scatter( x=['2021年'], y=[regr.predict(XXX_)[-1]], mode='markers', name="2021年預測銷量" # 第一個圖例名稱 ) data = [trace1,trace2,trace3] layout = go.Layout(title='天貓淘寶雙十一歷年銷量', xaxis_title='年份', yaxis_title='銷量') fig = go.Figure(data=data, layout=layout) fig.show()
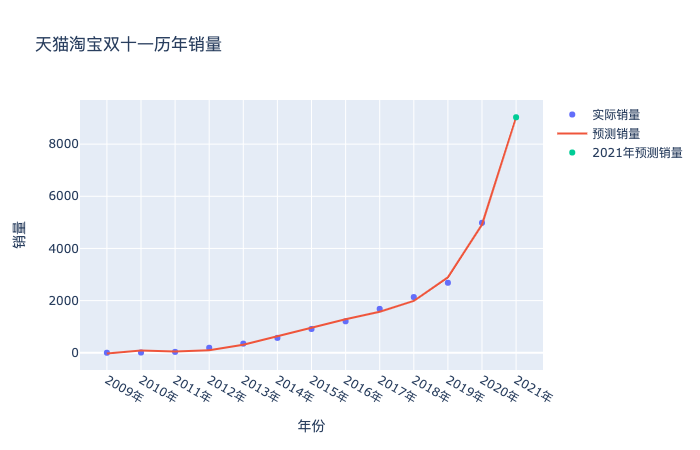
在選擇模型中的次數方面,可以通過設置程序,循環計算各個次數下預測誤差,然后再根據結果反選參數。
df_new = df.copy() df_new['年份int'] = df['年份int'].apply(lambda x: x[0]) df_new
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
# 多項式回歸預測次數選擇
# 計算 m 次多項式回歸預測結果的 MSE 評價指標并繪圖
from sklearn.pipeline import make_pipeline
from sklearn.metrics import mean_squared_error
train_df = df_new[:int(len(df)*0.95)]
test_df = df_new[int(len(df)*0.5):]
# 定義訓練和測試使用的自變量和因變量
train_x = train_df['年份int'].values
train_y = train_df['銷量'].values
# print(train_x)
test_x = test_df['年份int'].values
test_y = test_df['銷量'].values
train_x = train_x.reshape(len(train_x),1)
test_x = test_x.reshape(len(test_x),1)
train_y = train_y.reshape(len(train_y),1)
mse = [] # 用于存儲各最高次多項式 MSE 值
m = 1 # 初始 m 值
m_max = 10 # 設定最高次數
while m <= m_max:
model = make_pipeline(PolynomialFeatures(m, include_bias=False), LinearRegression())
model.fit(train_x, train_y) # 訓練模型
pre_y = model.predict(test_x) # 測試模型
mse.append(mean_squared_error(test_y, pre_y.flatten())) # 計算 MSE
m = m + 1
print("MSE 計算結果: ", mse)
# 繪圖
plt.plot([i for i in range(1, m_max + 1)], mse, 'r')
plt.scatter([i for i in range(1, m_max + 1)], mse)
# 繪制圖名稱等
plt.title("MSE of m degree of polynomial regression")
plt.xlabel("m")
plt.ylabel("MSE")MSE 計算結果: [1088092.9621201046, 481951.27857828484, 478840.8575107471, 477235.9140442428, 484657.87153138855, 509758.1526412842, 344204.1969956556, 429874.9229308078, 8281846.231771571, 146298201.8473966]
Text(0, 0.5, 'MSE')
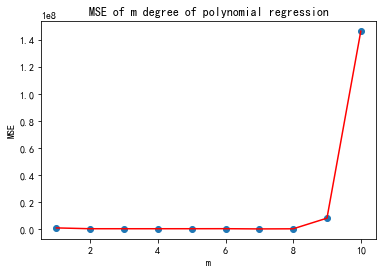
從誤差結果可以看到,次數取2到8誤差基本穩定,沒有明顯的減少了,但其實你試試就知道,次數選擇3的時候,預測的銷量是6213億元,次數選擇5的時候,預測的銷量是9029億元,對于銷售量來說,這個范圍已經夠大的了。我也就斗膽猜到9029億元,我的膽量也就預測到這里了,破萬億就太夸張了,歡迎膽子大的同學留下你們的預測結果,讓我們11月11日,拭目以待吧。
到此,相信大家對“怎么用Python爬蟲預測今年雙十一銷售額”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。